Уравнение плоскости в пространстве.

Задача 9. Построить уравнение плоскости, проходящей через точку А (1,2,3) перпендикулярно вектору 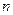(1,4,2)

Решение. Для произвольной точки 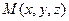в плоскости, вектор 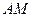с координатами 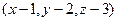ортогонален 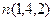. Их скалярное произведение 0. Тогда 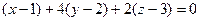, т.е.

.

Ответ. Уравнение плоскости .

Задача 10. Построить уравнение плоскости по точке (2,2,8) и перпендикуляру (3,3,7).

Решение.Как и в прошлой задаче, берём произвольную точку 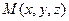в плоскости, тогда вектор 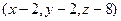ортогонален вектору . Тогда из чего следует .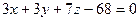

Ответ. .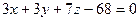

Задача 11.То же самое с произвольными параметрами.

Задача 12. Построить уравнение плоскости по точке 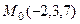и двум направляющим векторам (4,2,3) и .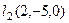

Решение. Способ 1.Сначала можно найти нормаль как векторное произведение: 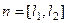, а затем уравнение плоскости по точке и нормали.

= = .

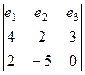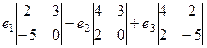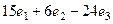Итак, нормаль 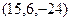, при этом можно заметить, что есть общий множитель 3, и поделить на 3, ведь от изменения длины, направление нормали не изменится. Итак, рассматриваем .

Теперь возьмём произвольную точку в этой плоскости, и проведём к ней вектор от точки 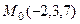. Это вектор 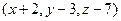. Он ортогонален вектору .

Тогда 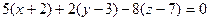, т.е. .

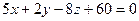Но это было решение в 2 этапа. А можно проще:

Способ 2. Возьмём вектор 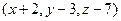в плоскости, тогда 3 вектора, а именно 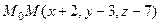, (4,2,3) и 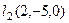должны образовывать линейно-зависимую систему. То есть, можем сразу найти такой определитель и приравнять к 0:

= = .

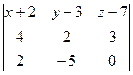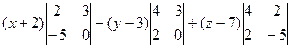Из этого следует . Такое уравнение можно сократить на 3, и получается .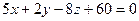

Ответ. .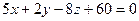

Задача 13. Построить уравнение плоскости, проходящей через (0,0,0) параллельно 2 направляющим (1,1,2) и (2,1,3).

Решение. Вектор от начала координат до произвольной точки 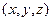, который сам имеет координаты 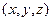, лежит в плоскости двух направляющих, т.е. определитель равен 0. = .

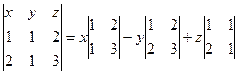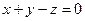Ответ. .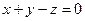

Задача 14. Построить уравнение плоскости по трём точкам. А(1,2,3), В(3,5,7), С(4,5,6).

Решение.Здесь можно одну из точек, например А, рассматривать в качестве основной, а две другие помогут найти 2 направляющих вектора: АВ и АС. АВ = (2,3,4), АС = (3,3,3).

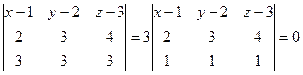
Для удобства вычислений, вынесли из определителя коэффициент 3.

Можно сразу сократить на него правую и левую часть.

Итак,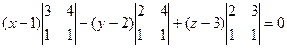

.

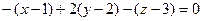
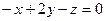Сократим ещё на 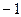, получим .

Ответ. .

Практика 12 (21 октября у обеих групп).

Плоскость. Прямая в пространстве.

Практика 13. Кривые и поверхности.

Практика 14. Повторение и контрольная работа.

Темы 2-й контрольной:

5. Векторная алгебра (скалярные, векторные произведения).

6. Системы уравнений, метод Гаусса

7. Собственные числа и векторы

8. Уравнения прямой и плоскости

Приложение 1.

Пример одного варианта контрольных работ.

Темы 1-й контрольной:

1. Действия над матрицами.

2. Определители.

3. Обратная матрица.

4. Ранг матрицы.

Вариант:

1) Умножить матрицы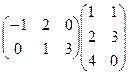

2) Найти определитель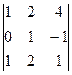

3) Найти обр.матрицу

4) Найти ранг матрицы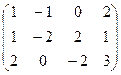

Темы 2-й контрольной:

5. Векторная алгебра (скалярные, векторные произведения).

6. Системы уравнений, метод Гаусса

7. Собственные числа и векторы

8. Уравнения прямой и плоскости

Вариант:

5) Векторы 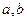выражены через : , .

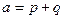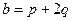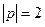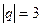, , угол между ними 60 градусов. Найти .

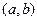6) Решить систему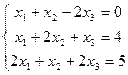

7) Найти собственные числа и собственные векторы линейного оператора, заданного матрицей .

8) Найти уравнение плоскости, проходящей через точку (1,4,2) перпендикулярно вектору (2,1,2).

Литература.

[1]. Магазинников Л.И. Практикум по линейной алгебре и аналитической геометрии.

[2].

[3].