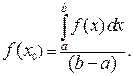Площадь криволинейной трапеции
Интеграл Римана
Представим, что мы должны подсчитать площадь земельного участка, изображенного на рисунке.
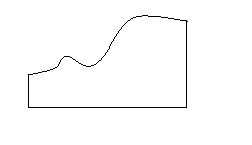
Такая фигура, ограниченная с трех сторон отрезками прямых, два из которых перпендикулярны третьему, а четвертая сторона пересекается прямой, перпендикулярной противоположному отрезку, только в одной точке, называется криволинейной трапецией. Очевидно, что любая плоская фигура может быть разбита на конечное число криволинейных трапеций. Будем считать, что прямолинейные участки сторон нашей криволинейной трапеции так же, как на рисунке, параллельны координатным осям. В этом случае можно нижний отрезок считать отрезком оси абсцисс, где 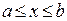 , и точки криволинейного участка задать с помощью непрерывной функции
, и точки криволинейного участка задать с помощью непрерывной функции 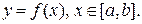
Для того, чтобы найти площадь криволинейной трапеции, заменим трапецию объединением прямоугольников по следующей схеме.
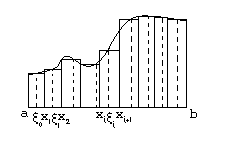
Отрезок 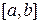 разделен на
разделен на 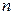 отрезков
отрезков 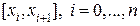 , где
, где 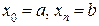 . На каждом отрезке выбрана точка
. На каждом отрезке выбрана точка 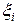 и в этой точке восстановлен перпендикуляр (прерывистая линия) до пересечения с кривой
и в этой точке восстановлен перпендикуляр (прерывистая линия) до пересечения с кривой 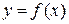 . Таким образом, вершиной перпендикуляра является точка с координатами
. Таким образом, вершиной перпендикуляра является точка с координатами 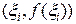 . На каждом отрезке
. На каждом отрезке 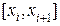 как на основании построен прямоугольник высотой
как на основании построен прямоугольник высотой 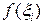 . Очевидно, что чем меньше отрезок
. Очевидно, что чем меньше отрезок 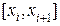 , тем меньше площадь прямоугольника отличается от площади криволинейной трапеции с основанием
, тем меньше площадь прямоугольника отличается от площади криволинейной трапеции с основанием 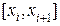 . Обозначим
. Обозначим 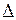 длину наибольшего из отрезков
длину наибольшего из отрезков 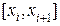 .
. 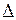 называется диаметром разбиения. Чем меньше диаметр разбиения, тем ближе сумма площадей построенных прямоугольников к площади исходной криволинейной трапеции с основанием
называется диаметром разбиения. Чем меньше диаметр разбиения, тем ближе сумма площадей построенных прямоугольников к площади исходной криволинейной трапеции с основанием 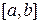 .
.
Итак, за приближенное значение площади исходной криволинейной трапеции возьмем 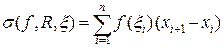 . Здесь
. Здесь 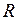 означает способ выбора точек разбиения
означает способ выбора точек разбиения 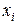 ,
, 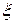 – выбор отмеченных точек
– выбор отмеченных точек 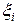 . Введенная сумма называется интегральной суммой Римана. Если существует предел
. Введенная сумма называется интегральной суммой Римана. Если существует предел 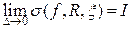 , причем этот предел не зависит ни от
, причем этот предел не зависит ни от 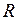 , ни от
, ни от 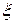 , то функция
, то функция 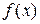 называется интегрируемой на отрезке
называется интегрируемой на отрезке 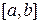 , а сам предел называется интегралом Римана по отрезку и обозначается
, а сам предел называется интегралом Римана по отрезку и обозначается 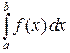 . Этот интеграл и будет равен площади криволинейной трапеции с основанием
. Этот интеграл и будет равен площади криволинейной трапеции с основанием 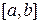 , ограниченной кривой
, ограниченной кривой 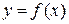 .
.
Любая непрерывная на отрезке функция является интегрируемой на этом отрезке. Хотя класс интегрируемых по Риману функций значительно шире, чем класс непрерывных функций, мы будем рассматривать только интегралы от непрерывных функций.
Пока непонятно, почему площадь криволинейной трапеции назвали интегралом – так же, как множество первообразных. Не видно связи между этими объектами. Тем не менее, связь есть. Отметим пока очевидные свойства интеграла Римана, следующие из свойств сумм и пределов.
1. Линейность. Если функции 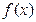 и
и 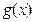 интегрируемы на отрезке
интегрируемы на отрезке 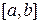 ,
, 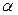 и
и 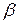 – произвольные постоянные, то функция
– произвольные постоянные, то функция 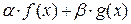 интегрируема на отрезке
интегрируема на отрезке 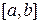 , причем
, причем 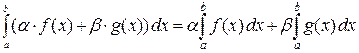 .
.
2. Аддитивность. Если функция 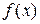 интегрируема на отрезке
интегрируема на отрезке 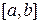 ,
, 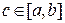 , то
, то 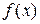 интегрируема на отрезках
интегрируема на отрезках 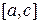 и
и 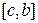 , причем
, причем 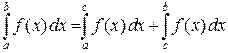 . Следствием этой формулы можно считать соотношение
. Следствием этой формулы можно считать соотношение 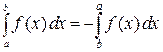 . То есть, замена направления интегрирования приводит к замене знака у интеграла.
. То есть, замена направления интегрирования приводит к замене знака у интеграла.
3. Интегральное неравенство. Если 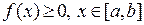 , то
, то 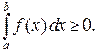
3-а. Если 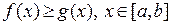 , то
, то 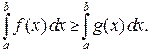
3-б. 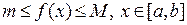 , то
, то 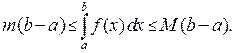
4. Теорема о среднем. Для любой непрерывной на отрезке 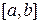 функции
функции 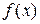 существует такая точка
существует такая точка 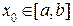 , что
, что 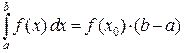 . То есть, существует равновеликий криволинейной трапеции прямоугольник на том же основании с высотой, равной значению функции в промежуточной точке.
. То есть, существует равновеликий криволинейной трапеции прямоугольник на том же основании с высотой, равной значению функции в промежуточной точке.
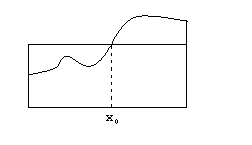
Доказательство. В соответствии со свойством 3-б 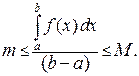
В силу свойства непрерывной функции существует такая точка 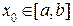 , что
, что