Предпосылки метода наименьших квадратов

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но, являясь лишь оценками, они не позволяют сделать вывод, насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей генеральной совокупности, насколько близки оценки a и b коэффициентов своим теоретическим прототипам a и β, как близко оцененное значение 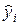к условному математическому ожиданию 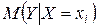, насколько надежны найденные оценки. Для ответа на эти вопросы необходимы определенные дополнительные исследования.

Как следует из соотношения (3.2), значения у_i зависят от значений x_i и случайных отклонений ε_i. Следовательно, переменная Y является случайной величиной, напрямую связанной с ε_i. Это означает, что до тех пор, пока не будет определенности в вероятностном поведении ε_i, мы не сможем быть уверенными в качестве оценок.

Можно показать, что оценки коэффициентов регрессии – случайные величины, зависящие от случайного члена в уравнении регрессии.

Доказано, что для получения по МНК наилучших результатов необходимо, чтобы выполнялся ряд предпосылок относительно случайного отклонения.

Предпосылки МНК (условия Гаусса - Маркова)

1. Математическое ожидание случайного отклонения ε_i равно нулю для всех наблюдений: 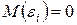для .

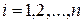Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения.

Для парной линейной регрессии эта предпосылка выполняется автоматически.

2. Дисперсия случайных отклонений ε_i постоянна для любых наблюдений i и j:

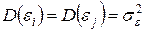
Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение).

Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).

3. Случайные отклонения ε_i и ε_j являются независимыми друг от друга для i ≠ j.

Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Другими словами, величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

Выполнимость данной предпосылки влечет следующее соотношение:

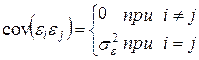
Поэтому, если данное условие выполняется, то говорят об отсутствии автокорреляции. С учетом выполнимости предпосылки 1. данное соотношение может быть переписано в виде: 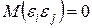для .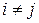

Причины невыполнимости данной предпосылки и проблемы, связанные с этим, рассматриваются ниже.

4. Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в данной модели.

Данное условие предполагает выполнимость следующего соотношения:

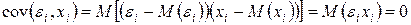
Следует отметить, что выполнимость данной предпосылки не столь критична для эконометрических моделей.

5*. Модель является линейной относительно параметров.

Для случая множественной линейной регрессии существенными являются еще две предпосылки.

6*. Отсутствие мультиколлинеарности.

Между объясняющими переменными отсутствует сильная линейная зависимость.

7*. Случайные отклонения ε_i , i = 1, 2, …, n, имеют нормальное распределение.

Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

Наряду с выполнимостью указанных предпосылок при построении классических линейных регрессионных моделей делаются еще некоторые предположения. Например:

• объясняющие переменные не являются случайными величинами;

• число наблюдений существенно больше числа объясняющих переменных (числа параметров уравнения);

• отсутствуют ошибки спецификации, т. е. правильно выбран вид уравнения и в него включены все необходимые переменные.

Часто полагают, что число наблюдений должно быть как минимум в 5-6 раз больше числа параметров уравнения (числа объясняющих переменных).

Выполнение 4-го условия Гаусса-Маркова обеспечивает несмещенность оценки параметра b. Выполнение 1-го и 4-го условий Гаусса-Маркова обеспечивает несмещенность оценки параметра а.

Если предпосылки 2 и 3 нарушены, т. е. дисперсия отклонений непостоянна и (или) значения ε_i и ε_j связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.

Нарушение одного из условий Гаусса-Маркова приводит к нарушению эффективности оценок, т. е. в классе несмещенных оценок можно найти такие, которые имеют меньшую дисперсию