Неопределимой рамы методом сил.
Заданная расчетная схема Исходные данные
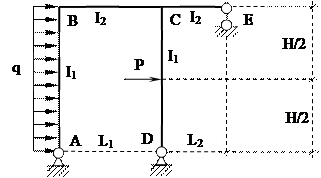 L1 = 6.0 м
L1 = 6.0 м
L2 = 4.0 м
H = 8.0 м
Р = 2 т
q = 1 т/м
I1 : I2 =2:3
E = const
1. Определение степени статической неопределимости заданной рамы.
Рама является внешне статически неопределимой системой , следовательно, степень статической неопределимости находится по формуле:
n = Соп –3 = 5 – 3 = 2
т.е. система дважды статически неопределима.
2. Выбор основной и эквивалентной систем метода сил. Назначение
лишних неизвестных Х1 и Х2
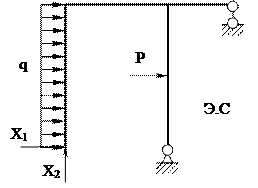 | |||
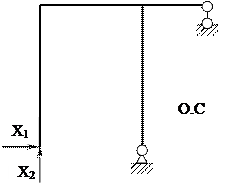 | |||
3. Система канонических уравнений будет иметь следующий вид:
 |
δ11Χ1 + δ12Χ2 + Δ1Р = 0,
δ21Χ1 + δ22Χ2 + Δ2Р = 0.
4. Построение единичных и грузовой эпюр изгибающих моментов.
Для построения единичных и грузовой эпюр необходимо для каждого состояния найти опорные реакции.
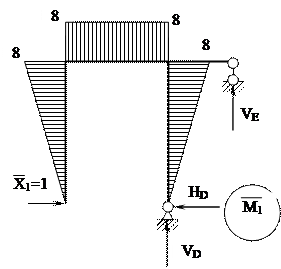 |
| |

 Σ X = 0, X1 – HD = 0, HD = 1
Σ X = 0, X1 – HD = 0, HD = 1
Σ Y = 0, VE + VD = 0, VD = 0
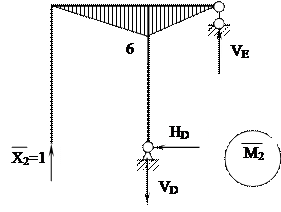 |
Σ МD = 0, X2 ·L1 -VE ·L2 = 0,
VE = 1,5
Σ X = 0, HD = 0,
Σ Y = 0, VE + X1 - VD = 0,
VD = 2,5
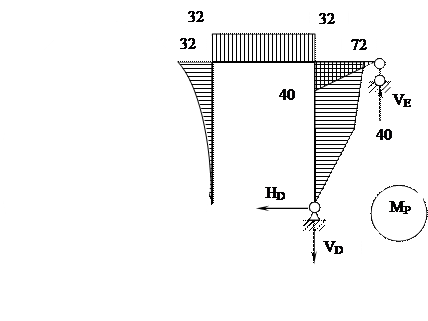
Σ МD = 0,
| |
 q ·H2/2 -VE ·L2 + P ·H/2 = 0,
q ·H2/2 -VE ·L2 + P ·H/2 = 0, Σ X = 0, q ·H + P – HD = 0,
HD = 10 (т)
Σ Y = 0, VE - VD = 0,
VD=10 (т)
5. Вычисление коэффициентов и свободных членов канонических уравнений.
δ11 = 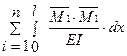 =
= 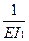 ·
·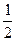 ·8·8·
·8·8·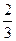 ·8·2 +
·8·2 +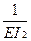 ·8·6·8 =
·8·6·8 =
= 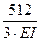 +
+ 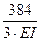 =
= 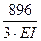
δ12 = 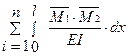 = -
= -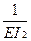 ·
·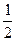 ·6·6·8 = -
·6·6·8 = - 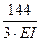 δ21 = δ12 = -
δ21 = δ12 = - 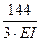
δ22 =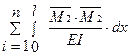 =
= 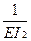 ·
·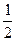 ·6·6·
·6·6· 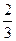 ·6 +
·6 +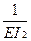 ·
·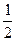 ·6·4·
·6·4· 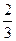 ·6 =
·6 =
= 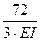 +
+ 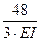 =
= 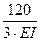
Δ1Р =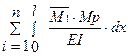 =
= 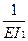 ·
·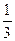 · 8 ·32 ·
· 8 ·32 ·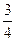 · 8 +
· 8 +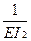 · 8 · 6 ·32 +
· 8 · 6 ·32 +
+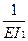 ·
·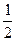 · 4 · 4 ·
· 4 · 4 · 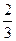 · 40 +
· 40 + 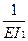 ·
· 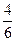 · (72·8 + 4·56·6 +4·40) =
· (72·8 + 4·56·6 +4·40) =
= 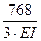 +
+ 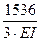 +
+ 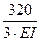 +
+ 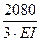 =
= 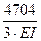
Δ2Р = 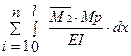 = -
= -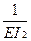 ·
·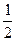 ·6·6·32 +
·6·6·32 + 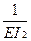 ·
·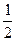 ·6·4·
·6·4· 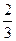 ·40 =
·40 =
= 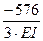 +
+ 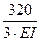 = -
= - 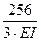
6. Построение суммарной единичной эпюры изгибающих моментов.


 МS = М1 + М2
МS = М1 + М2
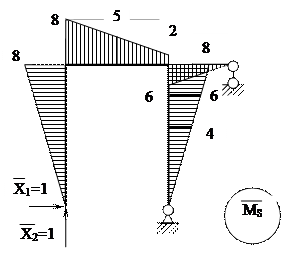 |
δSS = 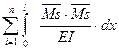 =
= 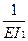 ·
·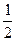 ·8·8·
·8·8· 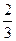 ·8·2 +
·8·2 +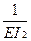 ·
·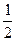 ·6·4·
·6·4· 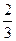 ·6 +
·6 +
+ 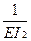 ·
· 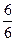 ·(8·8 + 4·5·5 + 2·2) =
·(8·8 + 4·5·5 + 2·2) = 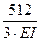 +
+ 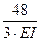 +
+ 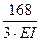 =
= 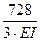
S δi j = δ11 + δ12 + δ21 + δ22 = 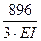 -
- 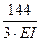 -
- 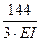 +
+ 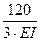 =
= 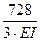
δSS = S δi j , т.е. выполнена универсальная проверка единичных коэффициентов, следовательно, единичные коэффициенты найдены верно.
7. Проводим проверку свободных членов канонических уравнений
( постолбцовая проверка).
ΔSР = 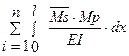 =
=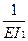 ·
·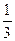 ·8·32·
·8·32·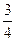 ·8 +
·8 + 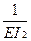 ·5·6·32 +
·5·6·32 +
+ 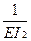 ·
·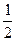 ·6 ·4·
·6 ·4· 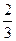 ·40 +
·40 + 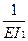 ·
· 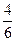 ·(40·4 + 6·4·56 +72·8) +
·(40·4 + 6·4·56 +72·8) + 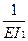 ·
·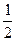 ·4·4·
·4·4· 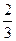 ·40
·40
= 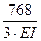 +
+ 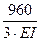 +
+ 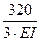 +
+ 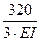 +
+ 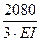 =
= 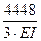
S ΔiР = Δ1Р + Δ2Р = 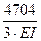 -
- 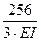 =
= 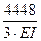
S ΔiР = ΔSР т.е. выполнена постолбцовая проверка , следовательно, свободные члены найдены верно.
8. Решаем систему канонических уравнений:
 |
896/(3·EI) ·Χ1 - 144/(3·EI) ·Χ2 + 4704/(3·EI) = 0,
-144/(3·EI) ·Χ1 + 120/(3·EI) ·Χ2 - 256/(3·EI) = 0.
Сократив оба уравнения на величину 8/(3·EI), получим следующую систему уравнений:
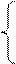 |
112 ·Χ1 - 18 ·Χ2 + 588 = 0,
-18 ·Χ1 + 15 ·Χ2 - 32 = 0.
 112 -18
112 -18
D0 = = 112·15 - 18·18 = 1356
-18 15
 -588 -18
-588 -18
D1 = = -588·15 + 18·32 = - 8244
32 15
 112 -588
112 -588
D2 = = 112·32 - 18·588 = - 7000
-18 32
Х1 = D1 / D0 = -8244 / 1356 = - 6,080 (т)
Х2 = D2 / D0 = -7000 / 1356 = -5,162 (т)
Делаем проверку найденного решения, т.е. подставляем полученные значения Х1 и Х2 в канонические уравнения:
112·(-6,080) – 18·(-5,162) + 588 = -588,004 + 588 = 0,004 » 0
- 18·(-6,080) +15 ·(-5,162) - 32 = 32,01 - 32 = 0,01 » 0
т.о. решение найдено верно.
9. Построение окончательной эпюры изгибающих моментов
 | |||
 |
Мок = М1·Х1 + М2·Х2 + МР
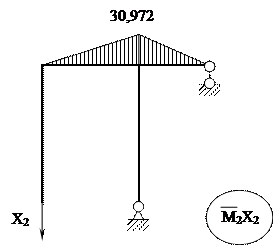 | |||||
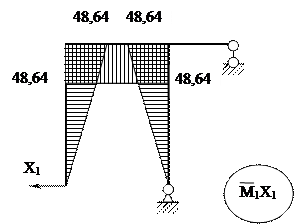 | |||||
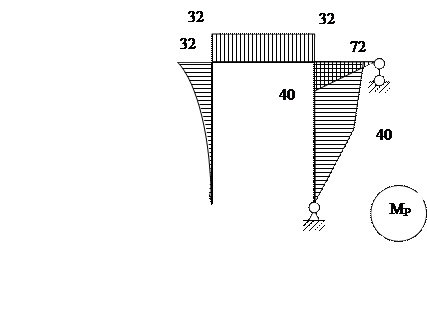 |
Проведем суммирование полученных эпюр по характерным точкам
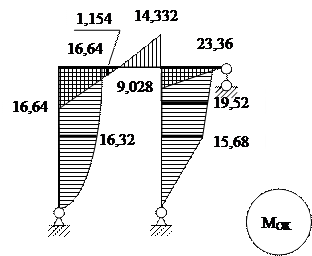 |
10. Проверяем правильность построения эпюры Мок
а) Статическая проверка:
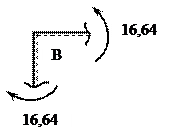 | |||
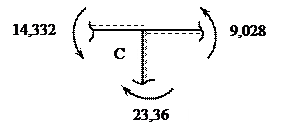 | |||
S МВ = 0, 16,64 - 16,64 = 0
S МС = 0, -23,36 + 14,322 + 9,028 = 0
б) Деформационная проверка:
Δ1ок =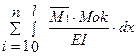 = -
= -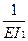 ·
· 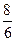 ·(0·0 + 4·4·16,32 + 16,64·8)-
·(0·0 + 4·4·16,32 + 16,64·8)-
-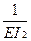 ·8·6·1,154 +
·8·6·1,154 + 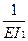 ·4/6·(15,68·4 + 4·6·19,52 +23,36·8)+
·4/6·(15,68·4 + 4·6·19,52 +23,36·8)+
+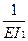 ·
·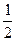 ·15,68·4·
·15,68·4· 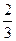 ·4 =
·4 =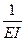 (-262,827-18,464 +239,36 +41,913)=
(-262,827-18,464 +239,36 +41,913)=
= 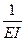 (-281,291 + 281,273) =
(-281,291 + 281,273) = 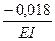 » 0
» 0
ОП: -0,018·100% /-281,291 = 0,006 % допустимая погрешность.
Δ2ок = 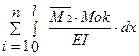 =
= 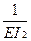 ·
· 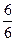 ·(0·16,64 + 4·3·1,154-14,332·6) +
·(0·16,64 + 4·3·1,154-14,332·6) +
+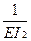 ·
·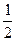 ·9,028·4·
·9,028·4· 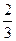 ·6 =
·6 = 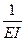 (-24,048 +24,075) =
(-24,048 +24,075) = 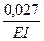 » 0
» 0
ОП: 0,027·100% / 24,075 = 0,11 % допустимая погрешность.
Деформационная проверка выполнена, следовательно, эпюра Мок
построена верно.
11. Построение эпюры поперечных сил на основании построенной эпюры изгибающих моментов Мок
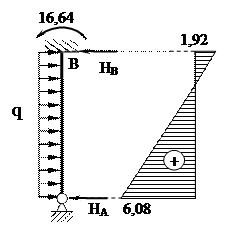 |
S МА = 0,
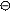 -16,64 + q·8·4 - НВ·8 = 0,
-16,64 + q·8·4 - НВ·8 = 0,
НВ = 1,92 (т)
S МВ = 0,
|
НА = 6,08 (т)
S Х = 0, -НА – НВ + q·8 = 0, 0 = 0
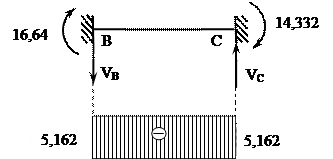 S МВ = 0,
S МВ = 0,
-VС·6 +14,332 +16,64 =0,
VС = 5,162 (т)
S МС = 0,
-VВ·6 +14,332 +16,64 =0,
VВ = 5,162 (т)
S Y = 0, VВ + VС = 0, 0 = 0
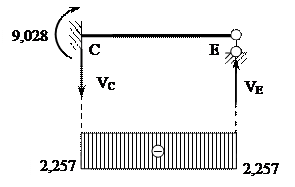
S МС = 0, 9,028 - VЕ·4 = 0
VЕ = 2,257 (т)
S МЕ = 0, 9,028 – VС·4 = 0
VС = 2,257 (т)
S Y = 0, -VС + VЕ = 0, 0 = 0
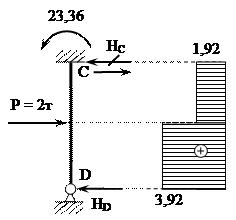 S МС = 0,
S МС = 0,
-23,36 + НD·8 - Р·4 = 0
НD = 3,92 (т)
S МD = 0,
-23,36 - НС·8 + Р·4 = 0
НС = -1,92 (т) – значит направление реакции выбрано неверно, поэтому меняем его на противоположное.
S Х = 0, -НD + НС +Р = 0, 0 = 0
Эпюра поперечных сил будет иметь следующий вид:
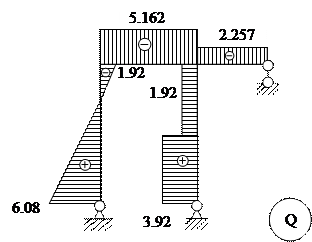 |
12. Построение эпюры продольных (нормальных) сил N , на основании построенной эпюры поперечных сил:
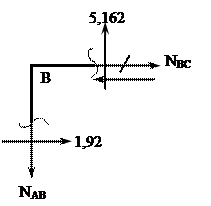 |
S Х = 0, NВС + 1,92 = 0
NВС = -1,92 (т)
Получается, что усилие NВС направлено в противоположную
сторону, т.е. в узел.
S Y = 0, -NАВ + 5,162 = 0
NВС = -1,92 (т)
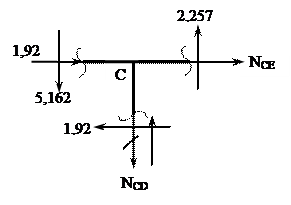 |
S Y = 0,
NСD - 5,162 + 2,257 = 0
NСD = -2,905 (т) направлено в противоположную сторону.
S Y = 0,
NСЕ - 1,92 + 1,92 = 0
NСЕ = 0
Эпюра продольных сил N будет иметь следующий вид:
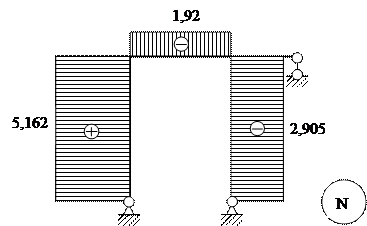 |
13. Согласно построенным эпюрам M, N, Q определяем опорные реакции рамы и составляем условие статического равновесия рамы в целом.
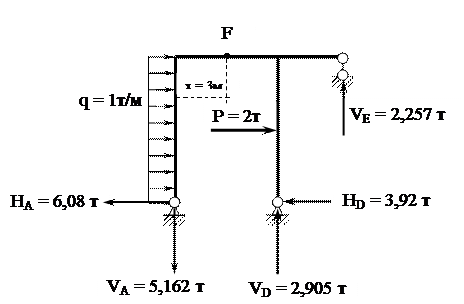 |
S М F = 0, -VА·3 + HА·8 - q ·8·4 - Р ·4 - VD·3 +HD·8 -VE·7 = 0,
-5,162·3 + 6,08·8 -1·8·4 - 2·4 - 2,905·3 +3,92·8 - 2,257·7 = 0,
0 = 0, следовательно, рама рассчитана верно, эпюры M, N, Q построены правильно.
Вопросы для самоконтроля.
1. Дать определение статически неопределимой рамы .
2. Дать определение внутренне и внешне статически неопределимых
рам.
3. Написать и пояснить формулы для определения степени
статической неопределимости внутренне и внешне статически
неопределимых рам.
4. Дать определение основной и эквивалентной систем.
5. Записать канонические уравнения метода сил для дважды
статически неопределимой системы. Объяснить физический смысл
каждого уравнения и каждого элемента входящего в уравнения.
6. Порядок определения единичных и грузовых коэффициентов
канонических уравнений.
7. Записать и пояснить проверки для единичных и грузовых
коэффициентов канонических уравнений.
8. Правила построения окончательной эпюры изгибающих моментов.
9. Деформационная проверка, ее физический смысл.
10. Порядок построения эпюры поперечных сил.
11. Порядок построения эпюры продольных усилий.
12. Взаимная проверка эпюр M, N, Q.
Общие указания
1. Расчетно-графическая работа должна быть выполнена на стандартных листах бумаги, формата А4 (210х297 мм).
2. Все записи и расчеты производятся чернилами на одной стороне листа, рисунки выполняются карандашом.
3. Расчеты должны содержать решения в общем (буквенном) виде и числовое решение.
4. Все вычисления производятся с точностью до 0,001.
5. Полностью выполненное и оформленное РГР сшивается и сдается преподавателя в указанные сроки.
Приложение 1
| Фигура | Площадь Ω | Абсциссы центра тяжести | |||
| Z1 | Z2 | ||||
| hl | l/2 | l/2 | |||
| hl/2 | l/3 | 2l/3 | |||
| hl/3 | l/4 | 3l/4 | |||
   
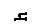 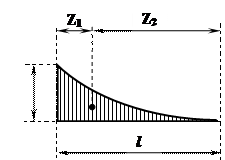 | hl (n+1) | l (n+2) | (n+1)l (n+2) | ||
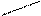
 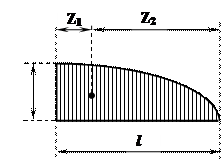 | 2hl/3 | 3l/8 | 5l/8 |
