Задачи, приводящие к понятию производной. Определение производной

Раздел III. Основы математического анализа в социально–экономической сфере.

Лекция 2Основы дифференциального исчисления

План:

1. Задачи, приводящие к понятию производной. Определение производной.

2. Экономический смысл производной.

3. Основные правила дифференциального исчисления. Производные основных функций.

4. Эластичность.

5. Примеры использования производной в социологии и психологии.

Задачи, приводящие к понятию производной. Определение производной.

Одним из основных понятий дифференциального исчисления является производная, которая используется при исследовании процессов, в том числе социологических и экономических, описываемых функциями.

Рассматривая различные по характеру задачи, мы приходим к пределу одного вида, который очень часто используется в различных областях науки. Поэтому ему дали отдельное название — производная. Дадим общее определение производной.

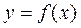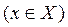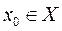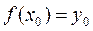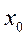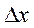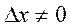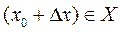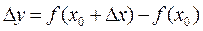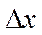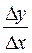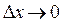Пусть функция определена на промежутке X . Выберем некоторую точку и найдём значение функции в этой точке: . Дадим приращение аргумента , такое, чтобы , и вычислим приращение функции , которое зависит от приращения аргумента . Найдём предел отношения при , то есть 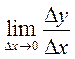. Если этот предел отношения приращения функции 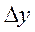к приращению аргумента 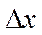при 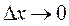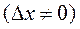существует и конечен, то он называется производной функции 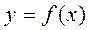в точке 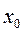. Производная имеет несколько обозначений: 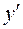, , 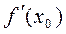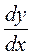. Следовательно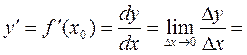 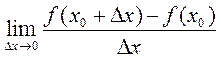. Нахождение производной функции 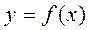называется дифференцированием этой функции. Функция, имеющая производную в точке 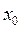, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках некоторого множества X, называется дифференцируемой на этом множестве.

Понятие производной возникло из двух на первый взгляд не связанных между собой задач: вычисления скорости и ускорениядвижущегося тела и построение касательной прямой к некоторой линии.

Дадим более подробное и точное определение мгновенной скорости. К моменту времени to пройденный путь равен s(to), а к моменту to+Δt — s(to+Δt). За промежуток времени Δt пройденный путь составит Δs=s(to+Δt) — s(to). Средняя скорость на промежутке Δs составит

.

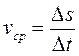Чем меньше Δt, тем лучше средняя скорость характеризует движение точки в момент времени to. Поэтому скоростью точки в момент to называют предел средней скорости за промежуток от to до to + Δt, когда 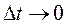, т. е. 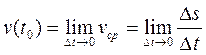. Нахождение мгновенной скорости 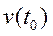в момент времени 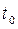сводится к нахождению производной 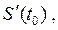то есть 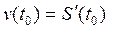где 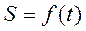– уравнение движения точки. Мгновенную скорость используют не только в физике. В социально-экономических задачах понятие мгновенной скорости используется при определении скорости роста объемов продукции, скорости распространения рекламы, скорости роста трудоспособного населения и т. п.

Ниже мы рассмотрим задачи из социально-экономической сферы, которые приводят к понятию производной.