Краткие теоретические сведения. Обыкновенное дифференциальное уравнение порядка n имеет вид: (*)
Обыкновенное дифференциальное уравнение порядка n имеет вид:
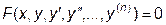 | (*) |
где 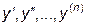 - производные первого, второго, ... , n -го порядков от искомой функции y. Его решением является семейство функций
- производные первого, второго, ... , n -го порядков от искомой функции y. Его решением является семейство функций
y = y(x,a1,a2,...,an),
где a1,a2,...,an - произвольные константы.
Например, простейшее дифференциальное уравнение 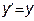 имеет решение y=aex. Каждому какому угодно значению параметра a соответствует своя функция, и все эти функции удовлетворяют исходному уравнению. имеет решение y=aex. Каждому какому угодно значению параметра a соответствует своя функция, и все эти функции удовлетворяют исходному уравнению. | 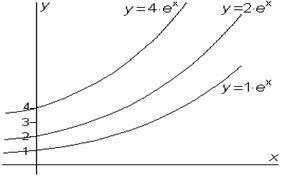 |
Если в дополнение к уравнению (*) задать конкретные значения
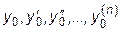
для некоторого значения x0 в виде
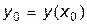 ; ; 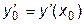 ; ; 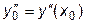 ;...; ;...; 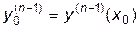 , , | (**) |
то тем самым определяется конкретный набор a1, a2, ... , an и, следовательно, единственная конкретная функция y(x,a1, a2, ... , an) из всего семейства решений.
Условия (**) называются начальными условиями, а вся задача, включающая дифференциальное уравнение (*) и начальные условия (**), называется "задачей Коши".
В задании 5 рассматривается решение задачи Коши для дифференциального уравнения первого порядка. Формулировка задачи звучит так: требуется решить дифференциальное уравнение 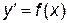 при начальных условиях
при начальных условиях 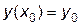 .
.
К сожалению, класс дифференциальных уравнений, позволяющих аналитическими методами получить решение, довольно узок. Например, уравнение y'=x2+y2 не имеет аналитического решения.
| При численном решении задачи Коши необходимо задаваться границами xнач, xкон изменения аргумента x и величиной h, являющейся шагом его изменения, который определяет дискретность вычисления значений функции y=y(x). Решение, полученное численным методом, есть таблица соответствующих значений (xi,yi), i = 0,1,2,...,n, где x0=xнач, xn= xкон; xi+1 = xi + h | 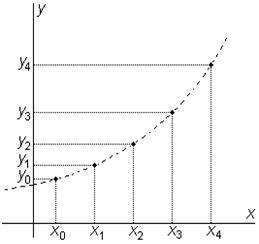 | x | y |
| x0 | y0 | ||
| x1 | y1 | ||
| x2 | y2 | ||
| x3 | y3 | ||
| x4 | y4 |
5.1.1. Метод Эйлера
Это простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. Его точность невелика, и поэтому на практике им пользуются сравнительно редко. Однако на основе этого метода легче понять алгоритмы других, более эффективных методов.
Считаем, что уже известно значение ym искомой функции y(x) в точке xm (m=1,2,3,…). Каждое следующее значение ym+1 в точке xm+1=xm+h определяется по формуле
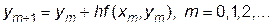
Вывод вычислительной формулы метода Эйлера и его геометрическая интерпретация даны в [ 1 ].
Метод Эйлера является методом первого порядка точности.
5.1.2. Метод Рунге-Кутта IV порядка.
Наиболее распространенным численным методом решения задачи Коши является метод Рунге-Кутта IV порядка, обеспечивающий достаточно высокую точность, которая с лихвой оправдывает дополнительное, по сравнению методом Эйлера и его модификациями, увеличение объема вычислительной работы. Расчеты при использовании этого классического метода производятся по формуле
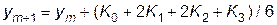 , , |
5.1.3.
| где | K0 = h f(xm, ym), |
| K1 = h f(xm+0.5h, ym+0.5K0), | |
| K2 = h f(xm+0.5h, ym+0.5K1), | |
| K3 = h f(xm+h, ym+K2). |
Задание
Изучить теоретический материал: численные методы решения дифференциальных уравнений.
Дано дифференциальное уравнение 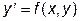 . Необходимо найти его решение методами Эйлера и Рунге-Кутта IV порядка при заданных начальных условиях y(x0)=y0 на заданном промежутке интегрирования [xнач,хкон] с шагом, вычисленным по формуле: h=(хкон-xнач)/20. Исходное уравнение, начальные условия и промежуток интегрирования выбираются из таблицы индивидуальных вариантов.
. Необходимо найти его решение методами Эйлера и Рунге-Кутта IV порядка при заданных начальных условиях y(x0)=y0 на заданном промежутке интегрирования [xнач,хкон] с шагом, вычисленным по формуле: h=(хкон-xнач)/20. Исходное уравнение, начальные условия и промежуток интегрирования выбираются из таблицы индивидуальных вариантов.
Для обеспечения возможности оценки точности методов в таблице для каждого дифференциального уравнения приведено также его точное, аналитическое решение y=y(x,C), где C – произвольная константа. Требуется определить значение C, при котором это решение удовлетворяет начальным условиям y(x0)=y0, и сформировать таблицу значений функции y(x,C) на промежутке [xнач,хкон] с шагом h.
В качестве результата требуется сформировать таблицу, содержащую следующие графы:
1) значения аргумента х;
2) решение, полученное методом Эйлера;
3) решение, полученное методом Рунге-Кутта 4-го порядка;
4) аналитическое решение y(x,C) уравнения;
5) ошибка метода Эйлера по сравнению с точным решением;
6) ошибка метода Рунге-Кутта по сравнению с точным решением.
Построить диаграмму с графиками решений по Эйлеру и по Рунге-Кутту.
Для защиты контрольной работы представить на компьютере EXCEL-файл решения задачи и рукописный отчет. В отчете по задаче 5 представить ответы на контрольные вопросы.
Пример решения задачи
Порядок выполнения работы поясним на примере решения дифференциального уравнения 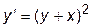 при начальных условиях y(0)=1 на промежутке [0; 0,7]. Общее решение данного уравнения имеет аналитический вид: y=tg(x+C)-x.
при начальных условиях y(0)=1 на промежутке [0; 0,7]. Общее решение данного уравнения имеет аналитический вид: y=tg(x+C)-x.
Введем заголовки таблицы и исходные данные:
A1’РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Скопируем из таблицы вариантов запись дифференциального уравнения и поместим ее как графический объект следом за введенным текстом.
А2’Общее решение
Скопируем из таблицы вариантов запись общего решения уравнения и поместим ее как графический объект следом за введенным текстом.
A3’Начальные условия: D3’Xo= E30 F3’Yo= G31
A4’Промежуток интегрирования: D4’Хн= E40 F4’Хк= G40,7
A5’Шаг интегрирования: D5’H= E5=(G4-E4)/20
A6’x B6’Эйлер С6’К0 D6’K1 E6’K2 F6’K3 G6’Р-К
H6’Точное I6’Ошибка Эйлера J6’Ошибка Р-К
Заполняем столбец значений аргумента х:
A7=E3 A8=A7+$E$5 Копируем А8 в А9:А27
Заполняем столбец решения по методу Эйлера:
B7=G3 B8=B7+$E$5*(A7+B7)^2 . Копируем B8 в B9:B27.
Заполняем столбцы решения по методу Рунге-Кутта:
G7=G3 C8=$E$5*(A7+G7)^2 D8=$E$5*(A7+0,5*$E$5+G7+0,5*C8)^2 E8=$E$5*(A7+0,5*$E$5+G7+0,5*D8)^2 F8=$E$5*(A7+$E$5+G7+E8)^2 G8=G7+(C8+2*D8+2*E8+F8)/6 Копируем C8:G8 в C9:G27.
Для построения столбца точного решения вычислим константу C, подставив в общее решение заданные начальные условия:
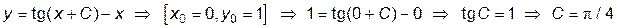 .
.
Занесем в таблицу вычисленную константу: F2’С= G2=ПИ()/4
Заполняем столбец точного решения:
H7=TAN(A7+$G$2)-A7 Копируем H7 в H8:H27.
Заполняем столбцы ошибок Эйлера и Рунге-Кутта:
I7=ABS(H7-B7) J7=ABS(H7-G7) . Копируем I7,J7 в I8:J27.
Построим совместные графики «метод Эйлера– метод Рунге-Кутта».
Полученная в результате описанных действий электронная таблица:
| A | B | C | D | E | F | G | H | I | J | |
| РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА | y′=(y+x)2 | |||||||||
| Общее решение: | y=tg(x+C)-x | С= | 0,7854 | |||||||
| Начальные условия: | Xo= | Yo= | ||||||||
| Промежуток интегрирования: | Хн= | Хк= | 0,7 | |||||||
| Шаг интегрирования: | H= | 0,035 | ||||||||
| х | Эйлер | К0 | К1 | К2 | К3 | Р-К | Точное | Ошибка Эйлера | Ошибка Р-К | |
| 1,00000 | 1,00000 | 1,00000 | 0,000000 | 0,000000 | ||||||
| 0,04 | 1,03500 | 0,03500 | 0,03749 | 0,03758 | 0,04027 | 1,03757 | 1,03757 | 0,002570 | 0,000000 | |
| 0,07 | 1,07507 | 0,04026 | 0,04314 | 0,04325 | 0,04635 | 1,08080 | 1,08080 | 0,005731 | 0,000000 | |
| 0,11 | 1,12096 | 0,04635 | 0,04969 | 0,04983 | 0,05344 | 1,13061 | 1,13061 | 0,009642 | 0,000000 | |
| 0,14 | 1,17357 | 0,05344 | 0,05733 | 0,05750 | 0,06174 | 1,18808 | 1,18808 | 0,014509 | 0,000000 | |
| 0,18 | 1,23396 | 0,06173 | 0,06631 | 0,06653 | 0,07153 | 1,25457 | 1,25457 | 0,020610 | 0,000000 | |
| 0,21 | 1,30344 | 0,07153 | 0,07696 | 0,07724 | 0,08320 | 1,33176 | 1,33176 | 0,028317 | 0,000000 | |
| 0,25 | 1,38361 | 0,08320 | 0,08970 | 0,09006 | 0,09724 | 1,42175 | 1,42175 | 0,038140 | 0,000000 | |
| 0,28 | 1,47644 | 0,09723 | 0,10510 | 0,10558 | 0,11432 | 1,52723 | 1,52723 | 0,050792 | 0,000000 | |
| 0,32 | 1,58442 | 0,11431 | 0,12395 | 0,12459 | 0,13539 | 1,65170 | 1,65170 | 0,067279 | 0,000000 | |
| 0,35 | 1,71069 | 0,13538 | 0,14736 | 0,14822 | 0,16177 | 1,79975 | 1,79975 | 0,089058 | 0,000000 | |
| 0,39 | 1,85932 | 0,16175 | 0,17689 | 0,17809 | 0,19540 | 1,97760 | 1,97760 | 0,118284 | 0,000001 | |
| 0,42 | 2,03561 | 0,19537 | 0,21488 | 0,21657 | 0,23919 | 2,19384 | 2,19384 | 0,158234 | 0,000001 | |
| 0,46 | 2,24666 | 0,23913 | 0,26486 | 0,26735 | 0,29765 | 2,46071 | 2,46071 | 0,214049 | 0,000002 | |
| 0,49 | 2,50212 | 0,29755 | 0,33245 | 0,33623 | 0,37814 | 2,79621 | 2,79622 | 0,294095 | 0,000005 | |
| 0,53 | 2,81547 | 0,37797 | 0,42696 | 0,43297 | 0,49329 | 3,22807 | 3,22808 | 0,412608 | 0,000011 | |
| 0,56 | 3,20603 | 0,49299 | 0,56479 | 0,57493 | 0,66625 | 3,80118 | 3,80120 | 0,595178 | 0,000025 | |
| 0,60 | 3,70243 | 0,66570 | 0,77695 | 0,79540 | 0,94334 | 4,59347 | 4,59353 | 0,891101 | 0,000062 | |
| 0,63 | 4,34881 | 0,94221 | 1,12802 | 1,16524 | 1,42855 | 5,75302 | 5,75320 | 1,404392 | 0,000183 | |
| 0,67 | 5,21641 | 1,42600 | 1,77107 | 1,85803 | 2,39725 | 7,59993 | 7,60060 | 2,384198 | 0,000676 | |
| 0,70 | 6,42709 | 2,39082 | 3,14403 | 3,39885 | 4,79015 | 10,97771 | 10,98137 | 4,554286 | 0,003661 | |
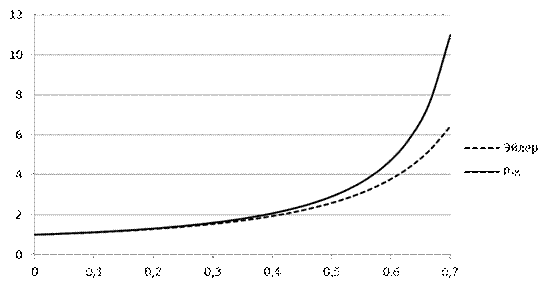 |
Таблица индивидуальных заданий
| № | Дифференциальное уравнение | Его аналитическое решение | Начальные условия | [xнач,хкон] |
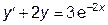 | 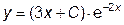 | y(0)=0.35 | [0, 2] | |
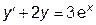 | 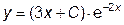 | y(0)=0.15 | [0, 2] | |
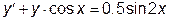 | 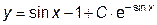 | y(0)=1.35 | [0, 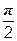 ] ] | |
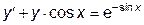 | 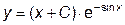 | y(0)=2.18 | [0, 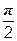 ] ] | |
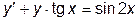 | 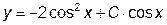 | y(0)=0.34 | [0, 0.7] | |
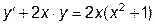 | 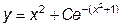 | y(0)=e | [0, 1] | |
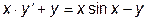 | 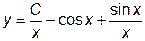 | 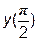 =1.0 =1.0 | [ 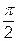 , , 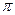 ] ] | |
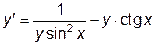 | 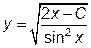 | y( 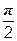 )=1 )=1 | [ 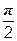 , , 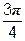 ] ] | |
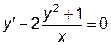 | 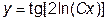 | y(1)=0 | [1, 2] | |
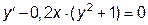 | 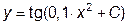 | y(0)=1.0 | [0, 2] | |
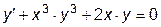 | 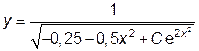 | y(0)=2.0 | [0, 0.6] | |
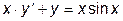 | 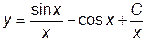 | 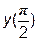 =1.0 =1.0 | [ 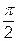 , , 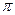 ] ] | |
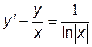 | 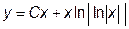 | y(e)=1.0 | [e, 2e] | |
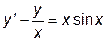 | 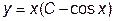 | 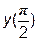 =1.0 =1.0 | [ 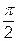 , , 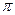 ] ] | |
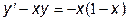 | 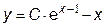 | y(1)=0.5 | [1, 2] | |
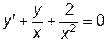 | 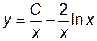 | y(1)=1.25 | [1, 20] | |
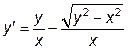 | 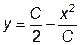 | y(1)=0 | [1, 2] | |
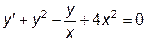 | 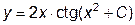 | y(0.5)=0 | [0.5, 1.3] | |
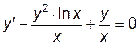 | 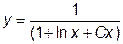 | y(1)=0.25 | [1, 20] | |
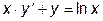 | 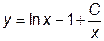 | y(1)=1.15 | [1, 20] | |
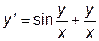 | 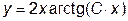 | y(1)= p | [1, 10] | |
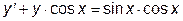 | 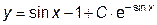 | y(0)=-1.5 | [0, 3] | |
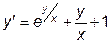 | 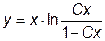 | y(1)=0 | [1, 1.5] | |
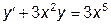 | 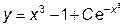 | y(0)=1.55 | [0, 2] | |
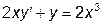 | 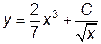 | 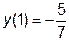 | [1, 10] | |
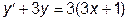 | 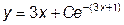 | y(0)=e | [0, 1] | |
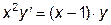 | 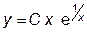 | y(1)=2.0 | [1, 10] | |
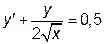 | 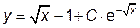 | y(1)=1.0 | [1, 10] | |
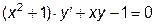 | 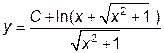 | y(0)=1.2 | [0, 10] | |
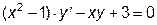 | 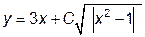 | y(2)=2.0 | [2, 10] | |
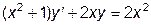 | 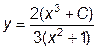 | y(0)=1.0 | [0, 10] | |
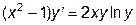 | 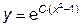 | y(2)=1.1 | [2, 10] | |
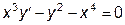 | 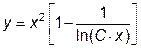 | y(1)=0 | [1, 20] | |
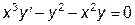 | 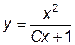 | y(1)=0.5 | [1, 10] |
5.5. Контрольные вопросы
1. Что является решением дифференциального уравнения?
2. Что является решением задачи Коши?
3. В чем заключается трудность численного решения задачи Коши с помощью рядов Тейлора?
4. Почему методы решения задачи Коши, использованные в данной работе, называются одношаговыми?
5. Каковы порядки точности использованных методов?
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Ершов М.Н. Численные методы решения задач: Конспект лекций. / М.Н. Ершов.–Керчь: КГМТУ, 2013,–59с.
2. Мудров А.Е. Численные методы для ПЭВМ на языках Бэйсик, Фортран и Паскаль. / А.Е. Мудров.- Томск; : МП «РАСКО», 1991. - 272с.
3. Маликов В.Т., Кветный Р.Н. Вычислительные методы и применение ЭВМ. Учеб. пособие./ В.Т. Маликов, Р.Н. Кветный – Киев: Высшая школа,1989. - 213с
4. Самарский А.А. Численные методы. / А.А. Самарский, А.В.Гулин. – М.: Наука, 1989.
5. Волков Е.А. Численные методы. / Е.А. Волков. – М.: Наука,1987.
6. Воробьева Г.Н. Практикум по вычислительной математике. Учеб. пособие. / Г.Н. Воробьева, А.Н. Данилова. – М.:Высш.шк.,1990. – 208с.
7. Бахвалов Н.С. Численные методы. / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – М., Наука, 1987.
8. Калиткин Н.Н. Численные методы. / Н.Н. Калиткин. – М., Наука, 1978.
Ó Михаил Николаевич Ершов
ИНФОРМАТИКА
Методические указания по выполнению контрольной работы по разделу
«Численные методы решения задач»
для студентов 2 курса специальностей 26.05.05 «Судовождение», 26.05.06 «Эксплуатация судовых энергетических установок», 26.05.07 «Эксплуатация судового электрооборудования и средств автоматики» и направления 13.03.02 Электроэнергетика и электротехника
заочной формы обучения
Тираж_____экз. Подписано к печати_____________.
Заказ №________. Объем 1,7 п.л.
Изд-во ФГБОУ ВО «Керченский государственный морской технологический университет» 298309 г. Керчь, Орджоникидзе, 82.
