Теорема умножения вероятностей

Рассмотрим два события: А и В; пусть вероятности Р(А) и Р_А(В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

.

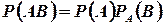Независимые события. Теорема умножения для независимых событий

Пусть вероятность события В не зависит от появления события А. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

.

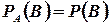Можно показать, что если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.

Для независимых событий теорема умножения имеет вид

Р(АВ) = Р(А)Р(В) , (**)

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Равенство (**) принимают в качестве определения независимых событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.

На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.

Пример. Найти вероятность совместного появления герба прн одном бросании двух монет.

Решение. Вероятность появления герба первой монеты (событие А)

Р (А) = 1/2.

Вероятность появления герба второй монеты (событие В)

Р (B) = 1/2.

События А и В независимые, поэтому искомая вероятность по теореме умножения равна

P(AB) = P(A) P(B) = 1/2 ∙1/2 = 1/4

Теорема сложения вероятностей совместных событий

Была рассмотрена теорема сложения для несовместных событий. Здесь будет изложена теорема сложения для совместных событий.

Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример. А - появление четырех очков при бросании игральной кости; В - появление четного числа очков. События А и В - совместные.

Пусть события А и В совместны, причем даны вероятности этих событий и вероятность их совместного появления. Как найти вероятность события
А + В, состоящего в том, что появится хотя бы одно из событий А и В? Ответ на этот вопрос дает теорема сложения вероятностей совместных событий.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р (А + В) = Р (А) + Р (В) — Р (АВ). (*)

Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми.

Для независимых событий

Р (А + В) = Р (А) + Р (В) - Р (А) Р (В);

для зависимых событий

Р(А + В) = Р(А) + Р(В) - Р(А)Р_А(В).

Замечание 2. Если события А и В несовместны, то их совмещение есть невозможное событие и, следовательно, Р(АВ) = 0.

Формула (*) для несовместных событий принимает вид

P(A+B) = P(A) + P(B).

Пример. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: р₁ = 0,7; р₂ = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы.

Вероятность события АВ (оба орудия дали попадание)

Р(АВ) = Р(А) Р (В) = 0,7∙ 0,8 = 0,56.

Искомая вероятность

Р(А + В) = Р(А) + Р (В) - Р (АВ) = 0,7 + 0,8 - 0,56 = 0,94.