Уравнения состояния идеальных и реальных газов
Реальные газы при низких давлениях близки к идеальным, так как в этом случае можно пренебречь силами межмолекулярного взаимодействия и объемом молекул. Это относится, в частности, к кислороду, азоту, водороду, воздуху, находящимся при высоких температурах и относительно низких давлениях. При нормальных условиях отклонение основных параметров состояния не превышает 3 %.
Именно идеальные газы подчиняются законам Бойля -Мариотта, Гей-Люссака и Авогадро.
1. Закон Бойля - Мариотта установлен опытным путем. Если постоянное количество газа, например 1 кг, при постоянной температуре (Т1 = Т2) будет переходить из одного состояния с параметрами р1 , υ1 в другое состояние с параметрами р2 , υ2 , то его давление будет изменяться обратно пропорционально объему
: 
Следовательно, при постоянной температуре произведение давления на объем данной массы газа есть величина постоянная.
2. Закон Гей-Люссака. Если нагревать или охлаждать одно и то же количество газа (1 кг) при постоянном давлении (р1 = = p2), то объем газа изменяется прямо пропорционально его абсолютной температуре:

3. Закон Авогадро. В равных объемах разных газов содержится одинаковое число молекул, если эти газы имеют одинаковые давление и температуру. Из закона Авогадро следует, что при одинаковых температурах и давлениях плотность газов пропорциональна их молекулярным массам:

Если принять, что μ - масса газа (кг), численно равная молекулярной массе, то
μυ = Vμ - объему 1 кмоля любого газа. При нормальных условиях
(р = 760мм рт. ст., t = 0 °С)

В реальных газах в отличие от идеальных существуют илы межмолекулярного взаимодействия, поэтому в расчетах необходимо учитывать собственный объем молекул. В результате уже при условиях, незначительно отличающихся от нормальных, углекислый газ и некоторые другие газы практически не подчиняются законам идеальных газов.
Для равновесного состояния идеального газа существует однозначная зависимость между его основными параметрами р, υ и Т. Зависимость выражается уравнением Клапейрона:
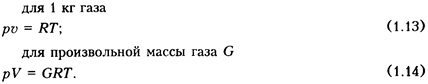
Уравнению (1.13) можно придать универсальную форму, если отнести газовую постоянную R, Дж/(кг • К), к 1 кмолю газа, т.е. при G = μ и, следовательно, V = Vμ

Впервые эта форма записи уравнения состояния предложена Д.И. Менделеевым, и оно получило название уравнения Менделеева - Клапейрона.
Величина μR, называется универсальной газовой постоянной, так как для всех газов и в любом состоянии она имеет одно и то же значение. Определим ее численное значение при р = 760 мм рт. ст. = 101325 Па; t = 0 °С:

Газовая постоянная

Как видно по единицам измерения, μR и R есть работа, которую совершает либо 1 кмоль, либо 1 кг газа при изменении температуры на 1К при постоянном давлении.
ГАЗОВЫЕ СМЕСИ
В практике в качестве рабочего тела используют, как правило, не какой-либо однородный газ, а газовую смесь: воздух, продукты сгорания различных видов топлива, природные газы и т.п. Газовая смесь - это механическая смесь газов, в которой не происходит никаких химических реакций.
Газовые смеси рассматриваются как смеси идеальных газов подчиняющиеся законам идеальных газов: закону Дальтона и уравнению Менделеева - Клапейрона.
Закон Дальтона гласит: общее давление смеси равно сумм» парциальных давлений отдельных газов, входящих в смесь.
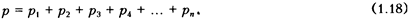
где p1 , р2 , . . . , рn- парциальные давления.
Парциальное давление - это давление, которое имел бы каждый газ, входящий в состав смеси, если бы он находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси.
Если при определенной температуре смеси поднять давление какого-либо из ее компонентов до давления смеси, то oн займет объем, называемый парциальным.
При расчете газовой смеси надо знать значения величин характеризующих ее газовую постоянную Rсм плотность ρсм , молекулярную массу (кажущуюся) μсм и др.
Состав смеси может быть задан или массами компонентов, или их объемами, или массовыми и объемными долями. Иногда состав газовой смеси задается числом молей отдельных газов.
Массовой долей называется отношение массы отдельного газа, входящего в состав смеси, к массе всей смеси. Если обозначить буквами g1 , g2 , g3 ,..., g4 массовые доли отдельных газов смеси, а буквами G1, G2, С3,...,G4 - массы этих газов, то массовые доли каждого из газов смеси составят
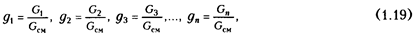
где

Очевидно, что сумма массовых долей равна единице:

Объемной долей называется отношение парциального объема отдельного компонента смеси к полному ее объему.
Если обозначить буквами r1, r2 , r3 , . . . rn ,объемные доли отдельных газов, а буквами V1 , V2 , V3 , . . . , Vn - приведенные (парциальные) объемы этих газов, то объемные доли 1, 2, 3,..., i-го газа смеси составят
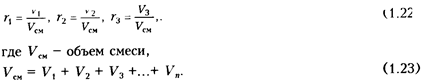
Значит, полный объем смеси Vсм равен сумме парциальных объемов ее компонентов. Из приведенных выше уравнений следует, что r1 + r2 + r3 + ...+rn =1.
Способ задания смеси числом молей тождествен заданию объемными долями.
Между массовыми и объемными долями существуют простые соотношения. Они позволяют производить пересчет состава смеси, заданной массовыми долями, в объемные и наоборот:
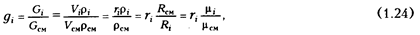
где ρi,, μi, Ri , ρсм , μсм , Rсм - соответственно плотность, молекулярная масса, газовая постоянная i-го компонента, плотность смеси, кажущаяся молекулярная масса и газовая постоянная смеси. Молекулярная масса смеси названа здесь кажущейся в связи с условностью этого понятия для смеси газов со своими молекулярными массами.
Согласно закону Авогадро плотности газов пропорциональны их молекулярным массам. Поэтому, решив уравнение (1.24), имеем

Газовая постоянная смеси Rсм может быть определена по уравнению

Пример 1. Определить плотность кислорода и азота пои нормальных условиях (760 мм рт. ст., 0 °С). Решение. По формуле (1.12)
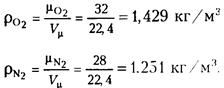
|

Пример 3. Атмосферный воздух содержит 20,97 % кислорода, 0,03 % углекислого газа и 79 % азота. При нормальных условиях определить плотность и кажущуюся молекулярную массу смеси. Решение.
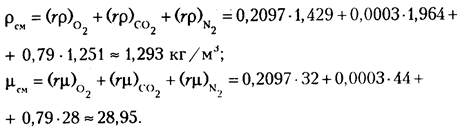
ТЕПЛОЕМКОСТЬ ГАЗОВ
Теплоемкостью (или удельной теплоемкостью) называется количество теплоты, которое необходимо при нагревании единицы количества газа (1 кг, 1 м3, 1 кмоль) для изменения температуры на 1 К в термодинамическом процессе.
