Условная вероятность. Независимость событий
Внимательный читатель наверняка обратил внимание на то, что в формуле вероятности суммы двух событий (теореме сложения) 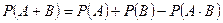 имеется слагаемое
имеется слагаемое 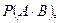 т.е. вероятность произведения двух событий, а мы об этом еще ничего не сказали. Это весьма важный момент, к которому мы и приступаем.
т.е. вероятность произведения двух событий, а мы об этом еще ничего не сказали. Это весьма важный момент, к которому мы и приступаем.
Пусть в результате опыта могут произойти события 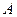 и
и 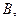 причем известны их вероятности
причем известны их вероятности 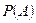 и
и 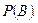 Предположим теперь, что опыт произведен и известно, что произошло событие
Предположим теперь, что опыт произведен и известно, что произошло событие 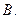 Изменит ли эта дополнительная информация начальную, доопытную (априорную) вероятность
Изменит ли эта дополнительная информация начальную, доопытную (априорную) вероятность 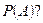 или она не меняется (хотя бы в некоторых случаях)?
или она не меняется (хотя бы в некоторых случаях)?
Пример 15. Подбрасывается игральная кость, т.е. 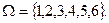 Рассмотрим следующие события: А = (выпадение четного числа) =
Рассмотрим следующие события: А = (выпадение четного числа) = 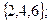 В = =(выпадение нечетного числа)=
В = =(выпадение нечетного числа)= 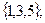 С=(выпадение четверки или шестерки)= =
С=(выпадение четверки или шестерки)= = 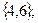 D=(выпадение не более пяти)={1,2,3,4,5};
D=(выпадение не более пяти)={1,2,3,4,5};
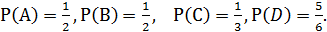 Рассмотрим несколько вариантов.
Рассмотрим несколько вариантов.
Пусть событие 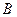 произошло, т.е. выпало нечётное число очков. Ясно, что при этом условии событие
произошло, т.е. выпало нечётное число очков. Ясно, что при этом условии событие 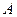 ( т.е выпадет чётное число) произойти не может, следовательно, априорная вероятность
( т.е выпадет чётное число) произойти не может, следовательно, априорная вероятность 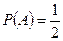 меняется.
меняется.
Определение. Вероятность события 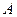 при условии, что событие
при условии, что событие 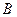 произошло (апостериорная вероятность), называется условной вероятностью события
произошло (апостериорная вероятность), называется условной вероятностью события 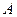 и обозначается
и обозначается 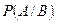
Для единообразия априорную вероятность 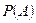 события
события 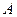 будем называть безусловной. Итак, в нашем примере
будем называть безусловной. Итак, в нашем примере 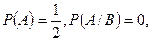 т.е.
т.е. 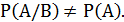
Пусть теперь событие 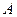 произошло. Вычислим
произошло. Вычислим 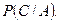 Если
Если 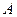 произошло, то выпало или 2, или 4, или 6. Из этих трех случаев событию
произошло, то выпало или 2, или 4, или 6. Из этих трех случаев событию 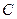 благоприятствуют два: 4 и 6. Заметим, что
благоприятствуют два: 4 и 6. Заметим, что 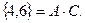 Таким образом, Р(С/А)=2/3. Аналогично, легко подсчитать, что Р(А/С)=1, Р(B/D)=3/5, Р(D/B)=1 и т.д.
Таким образом, Р(С/А)=2/3. Аналогично, легко подсчитать, что Р(А/С)=1, Р(B/D)=3/5, Р(D/B)=1 и т.д.
Определение. События 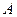 и
и 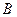 называются независимыми, если появление одного из них не влияет на вероятность появления другого. В противном случае события зависимые.
называются независимыми, если появление одного из них не влияет на вероятность появления другого. В противном случае события зависимые.
Условные вероятности определяются формулами:
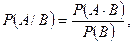
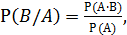 (7)
(7)
откуда получаем формулу вероятности произведения двух событий (теорему умножения).
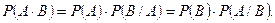 (8)
(8)
Отметим, что условная вероятность обладает всем свойствами вероятности.
В заключение запишем обобщенную формулу умножения вероятностей. Пусть имеем события 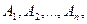 тогда
тогда
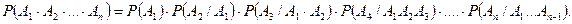 (9)
(9)
Если события независимые, то 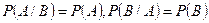 и формула (8) приобретает вид
и формула (8) приобретает вид 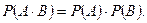
Заметим, что в примере 15 понять, зависимы или независимы события 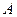 и
и 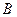 можно лишь перечислив составляющие их элементарные события. Дело в том, что в данном примере элементарные исходы взаимно исключают друг друга и связаны «одним прибором» - игральной костью, - они изначально зависимы. То же можно сказать о геометрических вероятностях. В других случаях зависимость или независимость событий ясна из физического (здравого) смысла. Например, составлена электрическая цепь из нескольких элементов. Выход из строя (или исправность) каждого элемента, разумеется, не зависит от других - они изначально независимы. При этом они, конечно, могут быть совместными - могут одновременно выйти из строя.
можно лишь перечислив составляющие их элементарные события. Дело в том, что в данном примере элементарные исходы взаимно исключают друг друга и связаны «одним прибором» - игральной костью, - они изначально зависимы. То же можно сказать о геометрических вероятностях. В других случаях зависимость или независимость событий ясна из физического (здравого) смысла. Например, составлена электрическая цепь из нескольких элементов. Выход из строя (или исправность) каждого элемента, разумеется, не зависит от других - они изначально независимы. При этом они, конечно, могут быть совместными - могут одновременно выйти из строя.
Именно с помощью теорем сложения и умножения, а так же используя формулы комбинаторики и решают задачи. Рассмотрим несколько примеров.
Пример 16. На карточках разрезной азбуки написаны буквы.
| а | а | б | б | б | о |
Карточки переворачивают, перемешивают и по порядку выкладывают. Найти вероятность того, что составится слово:
1) а б б а ; 2) б а о б а б
Решение. Первое задание. Будем решать двумя способами.
Первый способ ( по формулам комбинаторики). Обозначим А = ={составлено слово абба}, 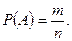 Число всех способов равно числу размещений (т.к. важен порядок следования букв) из 6 по 4:
Число всех способов равно числу размещений (т.к. важен порядок следования букв) из 6 по 4: 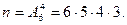 При вычислении числа
При вычислении числа 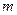 благоприятствующих случаев заметим, что слово «абба» содержит две буквы «а» и карточек таких тоже две. Если две карточки переставить местами, то слово не изменится, сделать это можно
благоприятствующих случаев заметим, что слово «абба» содержит две буквы «а» и карточек таких тоже две. Если две карточки переставить местами, то слово не изменится, сделать это можно 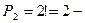 двумя способами. Для каждой такой перестановки в слове буквы «б» тоже можно переставить местами. Поскольку карточек с буквой «б» имеется три, то сделать это можно
двумя способами. Для каждой такой перестановки в слове буквы «б» тоже можно переставить местами. Поскольку карточек с буквой «б» имеется три, то сделать это можно 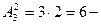 шестью способами. По основной формуле комбинаторики
шестью способами. По основной формуле комбинаторики 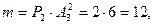 следовательно,
следовательно, 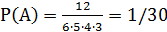 .
.
Второй способ (по теореме умножения)
Обозначим 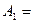 (первой извлечена буква
(первой извлечена буква 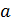 ),
), 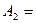 (второй извлечена буква б),
(второй извлечена буква б), 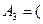 третьей извлечена буква б),
третьей извлечена буква б), 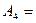 (четвертой извлечена буква
(четвертой извлечена буква 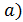 , тогда по формуле
, тогда по формуле 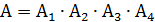 и по формуле (9)
и по формуле (9)
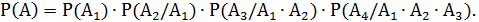 Вычислить все сомножители очень просто по классическому определению вероятности:
Вычислить все сомножители очень просто по классическому определению вероятности: 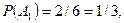 т.к. всего карточек 6, а благоприятствующих (с буквой «а») - две;
т.к. всего карточек 6, а благоприятствующих (с буквой «а») - две; 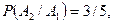 т.к. всего карточек осталось 5 (событие
т.к. всего карточек осталось 5 (событие 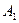 произошло), а благоприятствующих (букв «б») - три; аналогично,
произошло), а благоприятствующих (букв «б») - три; аналогично, 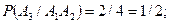
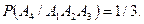 Получаем:
Получаем: 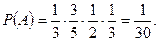
Второй способ мы изложили подробно, потратив много времени на запись решения – устно задачу можно решить этим способом очень быстро.
Второе задание также решим этими двумя способами.
Первый способ. Событие B = {составлено слово баобаб}, 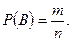 Рассуждая как в первом задании, получим ( без комментариев):
Рассуждая как в первом задании, получим ( без комментариев): 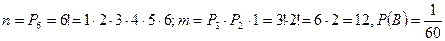
Второй способ ( без записи обозначений и комментариев):
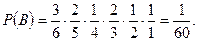 Читателю предлагается определиться, какой способ решения ему понравился больше.
Читателю предлагается определиться, какой способ решения ему понравился больше.
Пример 17. На книжной полке стоят 10 книг и среди них три тома С.А.Есенина. Книги нечаянно сброшены и наудачу расставляются на полку вновь. Какова вероятность события  состоящего в том, что три томика Есенина окажутся рядом.
состоящего в том, что три томика Есенина окажутся рядом.
Решение. Три томика Есенина будем обозначать звездочками (рис.8). Из рисунка ясно, что помеченная тройка книг среди других может занимать 8 позиций. При этом в каждой позиции можно переставлять 3 помеченные книги и 7 непомеченные, поэтому для искомой вероятности
 | ||||||||||||||||||||||||||||
 |  |  |  | |||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
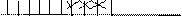 | ||||||||||||||||||||||||||||
 |  |  |  |  |  |  |  | |||||||||||||||||||||
Рис. 8 Рис. 9
| |
| |
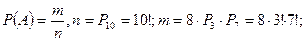
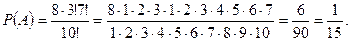
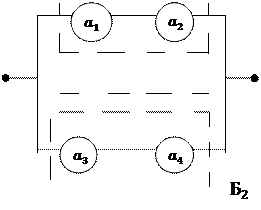
Пример 18. На рис. 9 представлена электрическая цепь. Известны вероятности 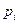 безотказной работы элементов цепи
безотказной работы элементов цепи 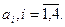 за время
за время 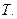 Найти вероятность безотказной работы цепи за время
Найти вероятность безотказной работы цепи за время 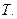
Решение. Обозначим события 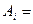 {безотказная работа элемента
{безотказная работа элемента 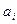 за время
за время 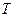 },
}, 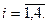 Пусть событие
Пусть событие 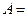 {безотказная работа цепи за время
{безотказная работа цепи за время 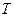 }.
}.
На рис.9 элементы 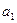 и
и 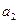 , соединенные последовательно, объединим в блок
, соединенные последовательно, объединим в блок 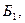 а элементы
а элементы 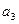 и
и 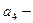 в блок
в блок 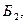 и обозначим события
и обозначим события 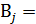 ={безотказная работа блока
={безотказная работа блока 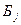 за время
за время 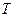 },
}, 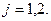 По схеме видно, что блоки
По схеме видно, что блоки 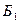 и
и 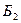 соединены параллельно. Тогда
соединены параллельно. Тогда 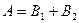 ( схема работает, если работает блок
( схема работает, если работает блок 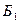 , или
, или 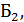 или оба). События
или оба). События 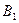 и
и 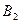 совместные, поэтому по теореме сложения
совместные, поэтому по теореме сложения
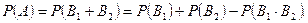 (10)
(10)
В каждом блоке элементы соединены последовательно, поэтому 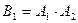 ( блок
( блок 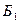 работает, если работает элемент
работает, если работает элемент 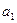 и
и 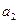 ). События
). События 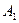 и
и 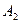 независимые, поэтому по теореме умножения
независимые, поэтому по теореме умножения 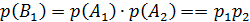 . Аналогично
. Аналогично 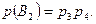 Подставляя в формулу (10), получим:
Подставляя в формулу (10), получим: 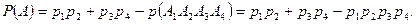
Например, если все 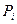 равны 0,9, то
равны 0,9, то 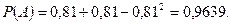
Замечание. По решению этой задачи акцентируем внимание читателя на следующем: если применяем теорему сложения, то следим – совместны или несовместны события; если применяем теорему умножения, то учитываем - зависимы или независимы сомножители!
Пример 19. Три стрелка произвели по одному выстрелу по мишени. Вероятности попадания для стрелков равны 0,9; 0,8 и 0,7. Найти: 1) вероятность того, что мишень будет поражена тремя выстрелами; 2) вероятность того, что мишень будет поражена двумя выстрелами; 3) вероятность того, что все три стрелка промахнутся; 4) вероятность того, что хотя бы один стрелок поразит мишень.
Рещение. Введём случайные события 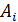 = {i-й стрелок поразил мишень}, i=1,2,3. По условию
= {i-й стрелок поразил мишень}, i=1,2,3. По условию 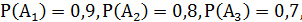 следовательно,
следовательно, 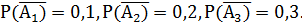
1) Обозначим событие В = {мишень поражена тремя выстрелами}. Это означает, что в мишень попал и первый, и второй, и третий стрелок, следовательно, В = 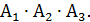 Разумеется, события
Разумеется, события 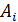 независимые, поэтому по теореме умножения
независимые, поэтому по теореме умножения 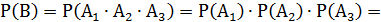
= 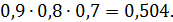
2) Обозначим событие С = {мишень поражена двумя выстрелами}, следовательно, 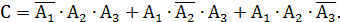 Тогда
Тогда
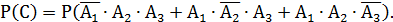
Заметим, что слагаемые в скобках являются попарно несовместимыми событиями, поскольку в каждой паре слагаемых есть событие и ему противоположное. Например, перемножим первое и второе слагаемые:
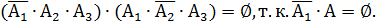
Следовательно, по аксиоме сложения, 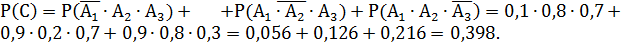
3) Обозначим событие Д = {все три стрелка промахнутся}, т.е. 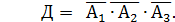 Тогда
Тогда 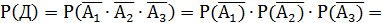
= 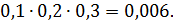
1) Обозначим событие Е = {хотя бы один стрелок поразит мишень}.Этот пункт примера можно решать по-разному.Рассмотрим их все. Во – первых, можно так рассуждать: событие Е означает, что в мишени окажется или одно попадание ( 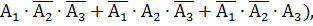 или два попадания (событие
или два попадания (событие 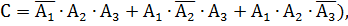 или три попадания (В =
или три попадания (В = 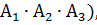 поэтому
поэтому 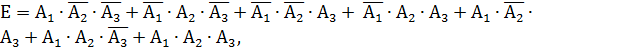
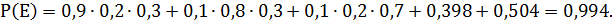
Во – вторых, можно рассуждать так: событие Е означает, что в мишень попал или первый стрелок, или второй, или третий. Тогда 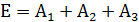 и по теореме сложения для трёх совместных событий получим:
и по теореме сложения для трёх совместных событий получим:
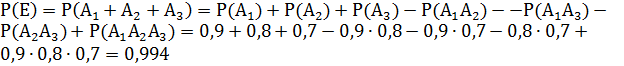
Наконец, рассмотрим самый рациональный способ: событие Е противоположно событию Д, т.е. 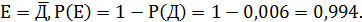
Пример 20. В лотерее «5 из 36» можно угадать 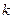 чисел
чисел 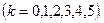 Чем больше угаданных чисел, тем больше выигрыш. Обозначим события
Чем больше угаданных чисел, тем больше выигрыш. Обозначим события 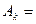 (угадано
(угадано 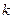 чисел),
чисел), 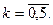 Вычислить
Вычислить 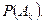
Решение. Каждую из вероятностей будем вычислять по классической схеме 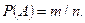 Вычислим, например,
Вычислим, например, 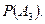 В лотерее каждый участник зачеркивает (выбирает) 5 чисел из 36. Поскольку порядок здесь не играет роли, число всех случаев
В лотерее каждый участник зачеркивает (выбирает) 5 чисел из 36. Поскольку порядок здесь не играет роли, число всех случаев 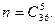 Благоприятствующими случаями для
Благоприятствующими случаями для 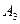 являются любые сочетания из 5 выигрышных чисел по три; при этом остальные два числа будут невыигрышными, т.е. число сочетаний из 31 невыигрышных числа по 2 элемента. Следовательно,
являются любые сочетания из 5 выигрышных чисел по три; при этом остальные два числа будут невыигрышными, т.е. число сочетаний из 31 невыигрышных числа по 2 элемента. Следовательно, 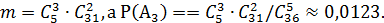
Аналогично вычисляются другие вероятности; приведем лишь результаты:
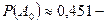 вероятность не угадать ни одного числа,
вероятность не угадать ни одного числа,
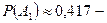 вероятность угадать одно число;
вероятность угадать одно число;
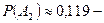 вероятность угадать два числа;
вероятность угадать два числа;
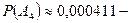 вероятность угадать четыре числа;
вероятность угадать четыре числа;
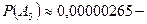 вероятность угадать все пять чисел и выиграть главный приз - шанс приблизительно три из миллиона!
вероятность угадать все пять чисел и выиграть главный приз - шанс приблизительно три из миллиона!
