Плоскорадиальный поток (приток к скважине)
Рисунок 2.3 – 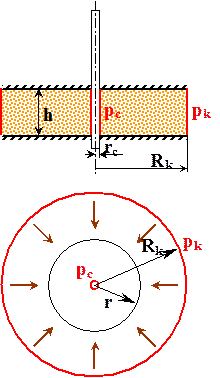 Схема притока к скважине |
Пусть в горизонтальном пласте постоянной толщины h и проницаемости k происходит фильтрация несжимаемой жидкости с вязкостью m к совершенной скважине радиусом rc, на которой поддерживается давление рс. На расстоянии Rk от скважины находится круговой контур питания, на котором поддерживается давление рk. (рисунок 2.3). Направим ось координат 0r от скважины. Для полного исследования такого потока, как было выяснено ранее, достаточно изучить движение жидкости вдоль оси 0r. Площадь поперечного сечения на радиусе r представляет боковую поверхность цилиндра и равна ω = 2 π r h.
Математическая постановка задачи описывается следующими уравнениями.
Уравнение неразрывности потока, которое при фильтрации несжимаемой жидкости удобно записать в интегральной форме:
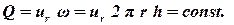 | (2.17) |
Законом фильтрации – законом Дарси, так как фильтрация происходит против направления оси 0r, то скорости фильтрации, а соответственно и расходы будут отрицательными, поэтому в законе Дарси опустим знак минус:
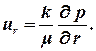 | (2.18) |
А также граничными условиями:
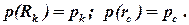 | (2.19) |
Требуется найти распределение давления по пласту и дебит скважины.
Для решения полученной задачи подставим закон Дарси в уравнение неразрывности, тогда получим дифференциальное уравнение первого порядка, которое легко интегрируется:
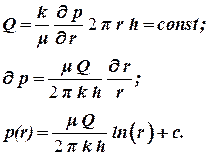 | (2.20) |
Из граничного условия на контуре питания получим:
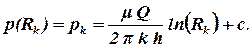 | (2.21) |
Для исключения постоянной интегрирования ‘c’ вычтем из уравнения (2.21) уравнение (2.20), при этом воспользуемся свойством логарифмов ln(Rk) ‑ ln(r) = ln(Rk/r):
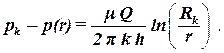 | (2.22) |
Тогда распределение давления по пласту запишется в виде:
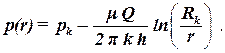 | (2.23) |
Откуда видно, что давление в пласте при плоскопараллельной фильтрации меняется по логарифмическому закону. Используя второе граничное условие, найдем дебит скважины:
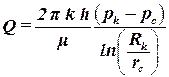 . | (2.24) |
Формулой для распределения давления (2.23) удобно пользоваться, если известно давление на контуре и дебит скважины. Если известны давления на контуре и на скважине, тогда удобнее из формулы (2.24) исключить расход:
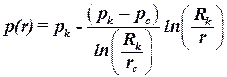 . | (2.25) |
При известных значениях давления на скважине и дебите получим:
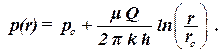 | (2.26) |
Скорость фильтрации можно найти или по закону Дарси, или используя уравнение неразрывности потока:
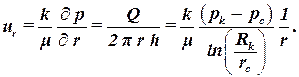 | (2.27) |
Из последнего выражения видно, что скорость фильтрации уменьшается обратно пропорционально расстоянию от скважины.
Рисунок 2.4 – 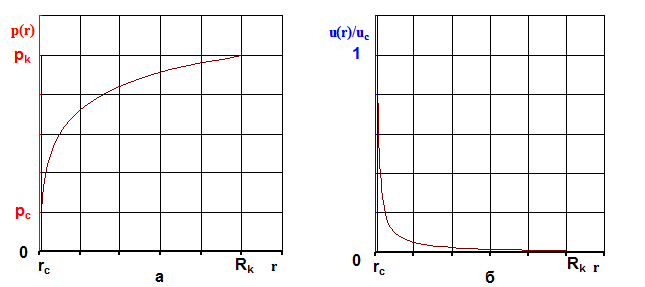 Распределение давления a) и отношение скорости фильтрации в пласте к скорости фильтрации на скважине б) для нефтяной скважины |
Найдем время вытеснения нефти водой при постоянном расходе галереи от контура питания до расстояния r. Считая вытеснение поршневым, получим, что за время t скважина добудет объем нефти Q t. Из пласта будет отобран объем нефти, которая находилась в порах пласта p (Rk2 – r2) h m. Так как эти объемы одинаковы, то:
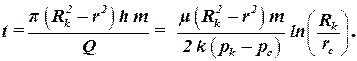 | (2.28) |
Полное время вытеснения нефти при поршневом вытеснении получим, если в последнюю формулу подставим r = rc.