Диэлектрики в электрическом поле. Ранее мы рассмотрели поведение проводников, в которых заряды под влиянием

Ранее мы рассмотрели поведение проводников, в которых заряды под влиянием электрического поля свободно текут в такие участки, что поле внутри проводника обращается в нуль. теперь мы будем говорить об изоляторах, т.е. таких материалах, которые не проводят электричество. Сначала можно было бы подумать, что в них вообще ничего не происходит. Но Фарадей с помощью простого электроскопа и конденсатора, состоящего из двух параллельных пластин, обнаружил, что это не так. Его опыт показал, что если между пластинами поместить изолятор, то емкость такого конденсатора увеличится. Когда изолятор целиком заполняет пространство между пластинами, емкость возрастает в e раз, причем e зависит только от свойств изолирующего материала. Изолирующие материалы называют также диэлектриками; тогда множитель e характеризует свойства диэлектрика и называется диэлектрической проницаемостью. Диэлектрическая проницаемость вакуума, конечно, равна единице.

Наша задача теперь состоит в том, чтобы объяснить, почему вообще возникает электрический эффект, раз изоляторы не проводят электричества. Начнем с экспериментального факта, что емкость увеличивается, и попытаемся разобраться, что же там может происходить. Рассмотрим плоский конденсатор, на проводящих пластинах которого имеются заряды, скажем, на верхней пластине отрицательные, а на нижней - положительные. Пусть расстояние между пластинами равно d, а площадь каждой пластины А. Как мы показали раньше, емкость равна

,

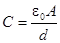а заряд и потенциал конденсатора связаны соотношением

Q = CV.

Далее, экспериментальный факт состоит в том, что если мы положим между пластинами кусок изолирующего материала, например стекла или плексигласа, то емкость возрастет. Это, разумеется, означает, что при том же заряде потенциал стал меньше. Но разность потенциалов есть интеграл от электрического поля, взятый поперек конденсатора; отсюда мы должны заключить, что электрическое поле внутри конденсатора стало меньше, хотя заряды пластин и не изменились.

Но как это может быть? Нам известна теорема Гаусса, которая утверждает, что полный поток электрического поля прямо связан с находящимся внутри объема электрическим зарядом. Рассмотрим входящую в теорему Гаусса поверхность S, изображенную пунктиром на рисунке. Поскольку электрическое поле в присутствии диэлектрика уменьшается, мы заключаем, что полный заряд внутри поверхности должен теперь быть меньше, чем до внесения изолятора. Остается сделать единственный вывод, что на поверхности диэлектрика должны находиться положительные заряды. Раз поле уменьшилось, но все же не обратилось в нуль, значит, этот положительный заряд меньше отрицательного заряда на проводнике. Итак, явление это можно объяснить, если мы поймем, почему на одной поверхности диэлектрика, помещенного в электрическое поле, индуцируется положительный заряд, а на другой - отрицательный.

Все было бы понятно, если бы речь шла о проводнике. Пусть у нас был бы, например, конденсатор, расстояние между пластинами которого равно d, и мы вставили бы между этими пластинами незаряженный проводник толщиной b. Электрическое поле индуцирует положительный заряд на верхней поверхности и отрицательный заряд на нижней поверхности, так что в результате поле внутри проводника погашается. Во всех остальных местах поле такое же, какое было без проводника, поэтому оно равно поверхностной плотности зарядов, деленной на e₀; но расстояние, по которому мы должны интегрировать, чтобы получить напряжение (разность потенциалов), стало меньше.

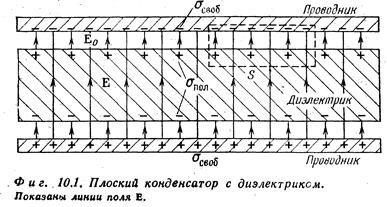
Напряжение равно

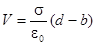
Окончательное выражение для емкости похоже на предыдущее, где d нужно заменить разностью (d - b):

.

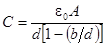Емкость увеличилась в некоторое число раз, зависящее от b/d, доли объема, занятого проводником.

Отсюда мы получаем модель того, что происходит в диэлектриках: внутри материала имеется множество мелких проводящих слоев. Беда такой модели состоит в том, что в ней должна иметься выделенная ось - перпендикуляр ко всем слоям, а у большинства диэлектриков такой оси нет. Эту трудность, однако, можно устранить, предположив, что все изолирующие материалы содержат маленькие проводящие шарики, отделенные один от одного изолятором. Появление диэлектрической проницаемости тогда объясняется действием зарядов, индуцируемых в каждом шарике. В этом и состоит одна из первых физических моделей диэлектриков, предложенная для объяснения явления, которое наблюдал Фарадей. Точнее, предполагалось, что каждый атом материала есть идеальный проводник, изолированный от остальных атомов. Диэлектрическая проницаемость e тогда должна была определяться долей того объема, который занимают шарики. Теперь, однако, пользуются другой моделью.

Продолжив наш анализ, мы обнаружим, что идея о проводящих и не проводящих участках не так уж существенна. Любой из маленьких шариков действует как диполь, момент которого создается внешним полем. Для понимания диэлектриков существенной является идея о том, что в материале возбуждается множество маленьких диполей. Почему они возникают - абсолютно не существенно.

Почему поле должно индуцировать дипольный момент у атома, хотя атом не является проводящим шариком? Перенесем рассмотрение этого вопроса на будущее. А сейчас мы дадим лишь один пример, только чтобы проиллюстрировать возможный механизм. Атом имеет ядро с положительным зарядом, окруженное отрицательными электронами. В электрическом поле ядро притягивается в одну сторону, а электроны в другую. Орбиты или плотности вероятности электронов (или какая-либо другая картина, используемая в квантовой механике) несколько искажаются; центр тяжести отрицательных зарядов сместится и больше не будет совпадать с положительным зарядом ядра. Если взглянуть на такой атом издалека, то подобная нейтральная конфигурация заряда в первом приближении эквивалентна маленькому диполю.

Если поле не чересчур велико, естественно считать величину индуцированного дипольного момента пропорциональной полю.

Предположим теперь, что в каждом атоме заряды q разделены промежутком d, так что qd есть дипольный момент одного атома. Если в единице объема имеется N атомов, то дипольный момент в единице объема равен Nqd. Этот дипольный момент в единице объема мы запишем в виде вектора Р. Направление вектора совпадает с направлением всех отдельных дипольных моментов, т.е. с направлением смещения зарядов d:

P = Nqd

Вообще говоря, Р будет меняться в диэлектрике от точки к точке. Но в каждой точке Р пропорционален электрическому полю Е. Константа пропорциональности, которая определяется тем, насколько легко можно сместить электрон, зависит от сорта атомов в материале.

Посмотрим теперь, что дает эта модель для конденсатора с диэлектриком. Рассмотрим сначала лист материала, в котором на единицу объема приходится дипольный момент Р.

Если положительные и отрицательные заряды, смещенные относительно друг друга, имеют одну и ту же среднюю плотность, то сам факт их смещения не приводит к появлению суммарного заряда внутри объема. С другой стороны, если бы Р в одном месте был больше, а в другом меньше, то это означало бы, что в некоторые области попало больше зарядов, чем оттуда вышло; тогда мы могли получить объемную плотность заряда. В случае плоского конденсатора предположим, что Р - величина постоянная, поэтому достаточно только посмотреть, что происходит на поверхностях. На одной поверхности отрицательные заряды (электроны) эффективно выдвинулись на расстояние d, а на другой поверхности они сдвинулись внутрь, оставив положительные заряды снаружи на эффективном расстоянии d. Возникает поверхностная плотность зарядов, которую мы будем называть поляризационным зарядом.

Итак, в электрическом поле на поверхности диэлектрика выступает нескомпенсированный заряд наведенных диполей.

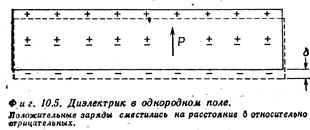
Дипольный момент на единицу объема называется вектором поляризации Р. Опыт показывает его пропорциональность электрическому полю:

Р= Nqd =ce₀E

q - заряд наведенных диполей;

d - эффективная расстояние между зарядами наведенных диполей;

N - количество диполей в единице объема;

c - диэлектрическая восприимчивость.

Поверхностная плотность s_пол поляризационных зарядов равна:

s_пол = Р×n, где n -единичныйвектор нормали к поверхности диэлектрика.

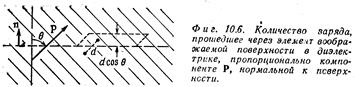
Суммарный поляризационный заряд DQ_пол , выступивший на произвольной (в том числе и на воображаемой) замкнутой поверхности диэлектрика равен:

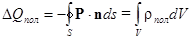, где V - объем диэлектрика, находящийся внутри поверхности S.

Заменяя по теореме Остроградского-Гаусса поверхностный интеграл объемным, получаем:

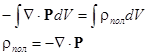
Если поляризация однородна, т.е. Р не зависит от координат, то ее дивергенция равна 0 и нескомпенсированный поляризационный заряд в объеме диэлектрика не появляется. Напротив, неоднородность поляризации вызывает появление нескомпенсированного поляризационного заряда в объеме диэлектрика.

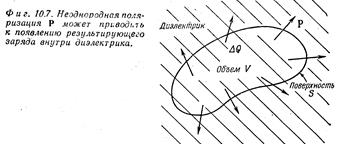
Уравнения электростатики для диэлектриков

Удобно условно разделить заряды на свободные и связанные. Связанными являются поляризационные поверхностные и объемные заряды, которые привязаны к атомам диэлектрика. Свободными являются все остальные заряды.

Используя первое уравнение Максвелла, справедливое во всех случаях, можно записать:

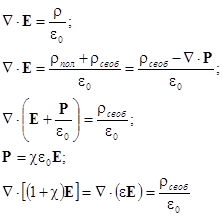
e = 1+c - диэлектрическая проницаемость диэлектрика

Вместо напряженности Е электрического поля в ряде случаев удобно ввести новую векторную величину D, называемую электрическим смещением, зависящую только от распределения свободных зарядов:

D= e₀E+P= ee₀E (последнее выражение является попыткой отразить свойства вещества с помощью диэлектрической проницаемости e, которая может в общем случае зависеть от напряженности поля, направления в пространстве, скорости изменения электрического поля и т.д.).

Для электрического смещения закон Гаусса выглядит так же, как и для напряженности электрического поля:

Ñ×D= r_своб

В задачах на нахождение электрического поля в диэлектриках, в которых однородный диэлектрик полностью заполняет пространство между зарядами, или напряженность электрического поля перпендикулярна границам диэлектрика, напряженность поля в диэлектрике может быть найдена как отношение напряженности Е₀ поля, которое было бы в данной точке пространства в отсутствие диэлектрика, к относительной диэлектрической проницаемости: Е = Е₀/e.

Пример случая, когда упомянутые условия не выполняются, показан на рисунке. В этом случае диэлектрик перекошен по отношению внешнему электрическому полю Е₀. Напряженность Е’ поля, создаваемого поляризационными зарядами на поверхности пластины диэлектрика, перпендикулярна граням пластины. Поэтому напряженность Е поля в диэлектрике и величина смещения D не совпадают по направлению с Е₀ и их численные значения сложным образом зависят от конфигурации системы.

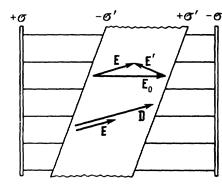
Поле в пластине диэлектрика, перекошенной относительно плоскостей, несущих сторонние заряды.

Условия на границе двух диэлектриков

Используя свойства электростатического поля (равенство 0 криволинейного интеграла от напряженности поля по замкнутому контуру и закон Гаусса), можно получить соотношение между нормальными и тангенциальными (по отношению к границе раздела диэлектриков с диэлектрическими проницаемостями e₁ и e₂) составляющими напряженности электрического поля и электрического смещения:

Е_1t = E_2t

D_1t/D_2t = e₁/e₂

E_1n/E_2n = e₂/e₁

D_1n = D_2n

Механизмы поляризации диэлектриков

Попробуем выяснить, почему вещество бывает диэлектриком. Как мы увидели, свойства электрических систем с диэлектриками можно было бы понять, предположив, что электрическое поле, действуя на диэлектрик, индуцирует в атомах дипольный момент. Именно, если электрическое поле Е индуцирует средний дипольный момент в единице объема Р, то диэлектрическая проницаемость дается выражением:

.

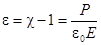Теперь нужно обсудить механизм возникновения поляризации внутри материала под действием электрического поля. Начнем с простого примера - поляризации газов. Существуют два типа газов. Молекулы некоторых газов, например кислорода, в каждой молекуле которого имеются два симметричных атома, лишены собственного дипольного момента. Зато молекулы других газов, вроде водяного пара (у которого атомы водорода и кислорода образуют несимметричную молекулу), обладают постоянным электрическим моментом. В молекуле водяного пара атомы водорода в среднем имеют положительный заряд, а атом кислорода - отрицательный. Поскольку центры тяжести положительного и отрицательного зарядов не совпадают, то распределение всего заряда в молекуле обладает дипольным моментом. Такая молекула называется полярной молекулой. А у кислорода вследствие симметрии молекулы центр тяжести и положительных и отрицательных зарядов один и тот же, так что это неполярная молекула. Она, правда, может стать диполем, если ее поместить в электрическое поле. Формы этих двух типов молекул нарисованы на рисунке.

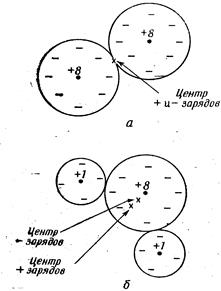
Электронная поляризация

Электронная поляризация определяет диэлектрическую проницаемость газов из неполярных молекул. Рассмотрим одноатомный газ. Точная теория атома, основанная на квантовой механике утверждает, что на электроны в атоме как бы действует линейная возвращающая сила. Для отклонения x от положения равновесия центра электронного заряда атома можно принять выражение: 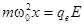. Где q_e - эффективный электронный заряд атома, w₀ - резонансная частота колебаний (известно, что тело массы m совершает гармонические колебания в случае линейной зависимости перемещения х от величины действующей силы F, в нашем случае F = q_eE. При этом частота гармонических колебаний определяется отношением коэффициента k в линейной зависимости перемещения от силы F = kx к массе тела: 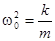). Отсюда следует линейная связь дипольного момента атома р и напряженности Е электрического поля:

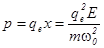
Или р= ae₀E, a - поляризуемость атома.

P= Np= Nae₀E=(e-1)e₀E;

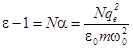
Таким образом, диэлектрическая проницаемость газов с симметричными молекулами, для которых существенна только электронная поляризация, должна зависеть от плотности газа и резонансной частоты w₀. Оценки показывают хорошее согласие теории и эксперимента. Диэлектрическая проницаемость таких газов мало отличается от 1.

Ориентационная поляризация

Характерна для газов из полярных молекул. Например, водяной пар.

Электрическое поле стремится выстроить отдельные диполи, создавая результирующий момент в единице объема. При обычных температурах и напряженностях поля столкновения молекул при их тепловом движении не позволяют им как следует выстроиться. Но некоторое выстраивание все же происходит, а отсюда и небольшая поляризация. Возникающая поляризация может быть подсчитана методами статистической механики.

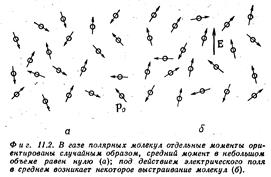
Потенциальная энергия диполя в электрическом поле

U = qj(1) - qj(2) = qd×Ñj = -p₀×E= -p₀Ecosq, где q - угол между p₀ и E.

Энергия становится меньше, когда диполи выстраиваются вдоль поля.

В состоянии равновесия, согласно распределению Больцмана, относительное число молекул с потенциальной энергией U пропорционально .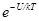

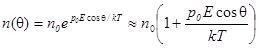(при обычных условиях показатель экспоненты мал). n(q)- концентрация молекул, приходящихся на единичный телесный угол

Интегрирование по всем углам q дает n₀. Если умножить n₀ на полный телесный угол 4p получим полное число молекул N в единице объема. Отсюда n₀ = N/4p. Чтобы вычислить Р, нужно знать векторную сумму всех молекулярных моментов в единице объема. Нужно просуммировать все компоненты р в направлении Е (компоненты, перпендикулярные Е при суммировании дадут 0).

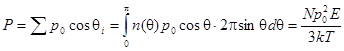~Е ~1/Т (закон Кюри).

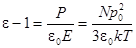
Диэлектрическая проницаемость полярных молекул сильно зависит от частоты внешнего поля. Молекулы инерционны и не успевают поворачиваться. Напротив, электронная поляризация остается практически неизменной вплоть до оптических частот. Например, диэлектрическая проницаемость воды, определяемая в основном ориентационной поляризацией, составляет на низких частотах 81, а на оптических частотах уменьшается в десятки раз.

Поляризация плотных веществ.

В плотных веществах необходимо учитывать вклад в поле, действующее на отдельный атом, поляризации атомов, находящихся по соседству. Необходимо различать среднее поле, равное V/d в конденсаторе, и поле действующее на отдельный атом.

Используя свойства электрического поля (равенство 0 криволинейного интеграла от напряженности поля по замкнутому контуру и закон Гаусса), можно доказать, что напряженность поля внутри длинной тонкой щели в диэлектрике зависит от ориентации этой щели относительно напряженности электрического поля. В случае перпендикулярного расположения щели и напряженности электрического поля находим, что поле Е₀ внутри щели равно Е₀ = Е + Р/e₀ , где Е - среднее поле в диэлектрике, Р - поляризация диэлектрика. Внутри продольной щели Е₀ = Е.

В большинстве жидкостей, не слишком сложных по своему строению, каждый атом в среднем так окружен другими атомами, что можно с хорошей точностью считать его находящимся в сферической полости. Можно доказать, что поле в сферической полости однородно и равно Е₀ = Е + Р/3e₀.

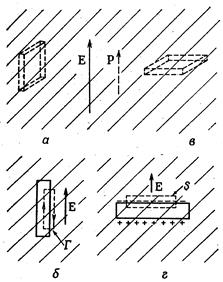
Поле внутри щели, вырезанной в диэлектрике, зависит от ее формы и ориентации.

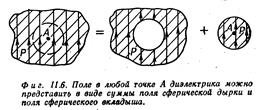
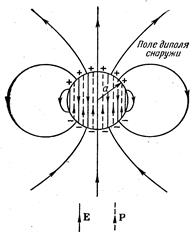
Электрическое поле однородно поляризованного шарика.

Сферическая полость дает поле, находящееся на 1/3 пути от поля параллельной щели к полю перпендикулярной щели. Отсюда:

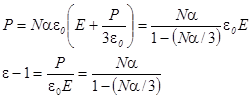
Последнее выражение носит название формулы Клаузиуса-Моссотти. Оно хорошо работает для неполярных жидкостей. В случае полярных жидкостей ситуация усложняется.

Если Na®3 диэлектрическая проницаемость стремится к ¥ за счет существования положительной обратной связи (увеличение поляризации атомов вызывает усиление влияния этой поляризации на соседние атомы, которые в свою очередь увеличивают поляризацию данных атомов). Такой эффект наблюдается в некоторых кристаллах (сегнетоэлектрики) при определенных температурах. Диэлектрическая проницаемость сегнетоэлектриков достигает при определенных температурах десятков тысяч.