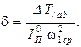Определение приведенных моментов сил сопротивления и движущих сил

Для рабочих машин приведенный момент движущих сил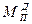

принимается постоянным ( 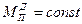), а приведенный момент сил сопротивления 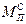определяется в результате приведения силы полезного сопротивления 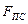и сил тяжести звеньев. Сила полезного сопротивления 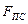, действующая на рабочий орган, определяется из механической характеристики технологического процесса. Чаще всего такая характеристика представлена в виде графической зависимости от хода ползуна 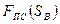. Для решения динамических задач необходимо получить зависимость 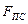от обобщенной координаты. Для этого производится привязка механической характеристики к крайним положениям ползуна в соответствии с технологическим процессом и ее обработка. Так, для показанной на рис. 1.7 механической характеристики процесса высадки рабочий ход происходит при движении ползуна слева направо (точки 6^/, 7…12, 13), а холостой ход – справа налево (точки 1, 2… 6, 6^/). Следует обратить внимание, что крайнее правое положение характеризуется двумя значениями силы 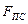: в начале холостого хода (пол. 1) 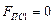, а в конце рабочего хода (пол. 13)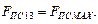

Рис. 1.7

Как отмечено ранее, приведенный момент сил 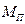представляется в виде алгебраической суммы

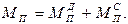
Определение 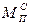выполняется из условия равенства мгновенных мощностей

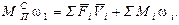
Откуда

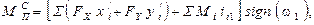(1.12)

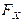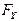где и - проекции силы 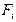на оси координат;

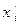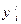и - проекции аналога скорости точки приложения силы ;

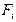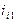- передаточная функция от i-го звена, к которому приложен момент 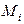, к звену 1;

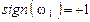при направлении вращения звена 1 против часовой стрелки;

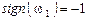- при направлении вращения звена 1 по часовой стрелке.

В формуле 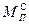(1.12) силы 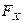, 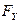и моменты 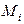берутся со знаками, соответствующими правой системе координат (положительное направление вращения – против часовой стрелки).

Так, для горизонтального механизма (рис. 1.8, а) 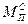определяется из равенства

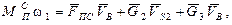
откуда

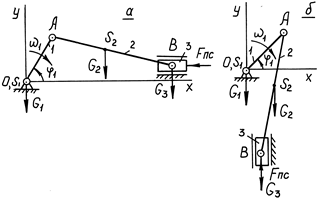Рис. 1.8

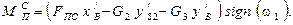
Учитывая, что 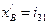, , 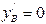, 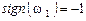получим

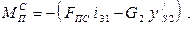
В рассматриваемом положении сила 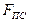имеет отрицательное значение, так как она направлена против положительного направления оси X.

Для вертикального механизма (рис. 1.8, б) аналогичным образом можно получить

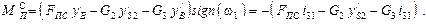
Сила 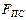в изображенном случае положительна.

Приведенный момент движущих сил 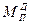определяется из условия, что при установившемся режиме движения изменение кинетической энергии машины за цикл равно нулю, т.е.

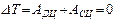, и за цикл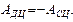

Работа сил сопротивления вычисляется как

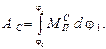
Интегрирование выполняется численным методом по правилу трапеций:

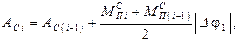
где 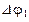- шаг интегрирования в радианах.

С учетом 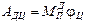при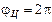

.

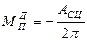1.2.3. Определение переменной составляющей приведенного момента инерции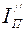

Переменная составляющая 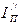определяется из условия равенства кинетических энергий, т.е. кинетическая энергия звена приведения, имеющего момент инерции 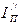, равна сумме кинетических энергий звеньев, характеризуемых переменными передаточными функциями:

.

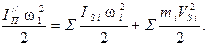Разделив это выражение на 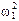, с учетом того, что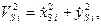

получим

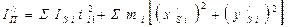
Для звеньев 2, 3 кривошипно-ползунного механизма (рис. 1.8)

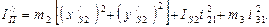
Производная 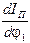, необходимая в последующем для определения закона движения звена приведения, имеет вид

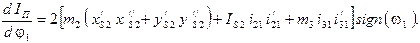
1.2.4. Определение постоянной составляющей приведенного момента инерции и момента инерции маховика

В основу расчета положен метод Н.И Мерцалова [4]. Для определения изменения кинетической энергии машины 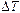предварительно определяем работу движущих сил 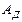. Для i-го положения

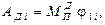
где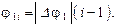

Тогда

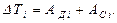
Изменение кинетической энергии 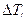звеньев с постоянным приведенным моментом инерции 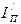равно

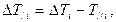
где 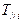- кинетическая энергия звеньев, создающих переменную составляющую 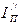. По методу Н.И. Мерцалова, 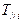определяется приближенно по средней угловой скорости :

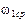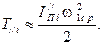
Далее из полученного за цикл массива значений 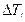(рис. 1.9) находим максимальную 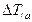и минимальную 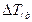величины, используя которые, вычисляем максимальный перепад кинетической энергии:

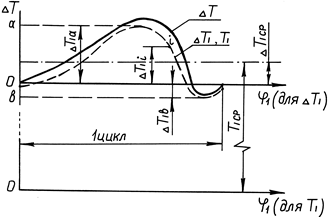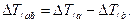
Рис. 1.9

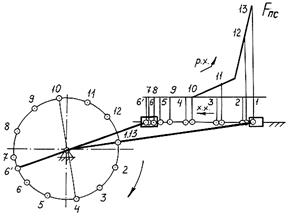
Тогда необходимая величина 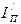, при которой имеет место вращение звена приведения с заданным коэффициентом неравномерности d , равна

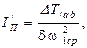где 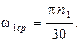(1.13)

Момент инерции маховика определяется как

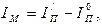
где 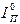- приведенный момент инерции всех вращающихся масс машины (ротора двигателя, зубчатых колес, кривошипа).

Иногда величина 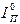может оказаться больше полученного значения 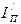. Это означает, что не требуется установки маховика. Реальный коэффициент неравномерности вращения в этом случае из (1.13) равен