Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Дифференциальное уравнение первого порядка и способ решения
Уравнение вида
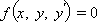 |
Называется обыкновенным дифференциальным уравнением первого порядка. Рассмотрим способы решения некоторых его типов.
Решением дифференциального уравнения первого порядка является функция 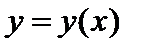 , которая непрерывна на промежутке X, имеет непрерывную производную и удовлетворяет данному уравнению тождественно относительно x.
, которая непрерывна на промежутке X, имеет непрерывную производную и удовлетворяет данному уравнению тождественно относительно x.
Способы решения.
Автономное уравнение
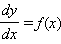 |
Домножим обе части уравнения на dx и проинтегрируем обе части получившегося уравнения: 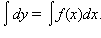 Таким образом,
Таким образом,
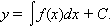 |
Уравнение с разделяющимися переменными
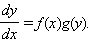 |
Это уравнение сводится к системе 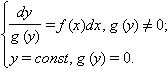 В первом уравнении после интегрирования находим y как неявную функцию от x:
В первом уравнении после интегрирования находим y как неявную функцию от x:
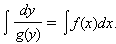 |
Однородное уравнение
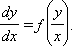 |
Пусть 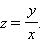 Тогда y = zx и
Тогда y = zx и 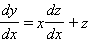 и
и
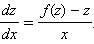 |
Задача сводится к решению уравнения с разделяющимися переменными, где F(x) = f(x) – z, 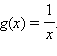
Линейное однородное уравнение
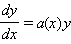 |
является уравнением с разделяющимися переменными и интегрируется по частям: 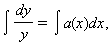 откуда
откуда
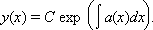 |
Линейное уравнение
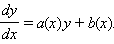 |
Будем искать решение этого уравнения в виде 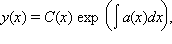 где C (x) – неизвестная функция. Тогда
где C (x) – неизвестная функция. Тогда 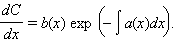 Вычисляя отсюда C (x) и подставляя эту функцию в предыдущее равенство, находим решение y (x).
Вычисляя отсюда C (x) и подставляя эту функцию в предыдущее равенство, находим решение y (x).
· Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у =j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Общим решением дифференциального уравнения первого порядка называется функция 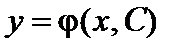 , зависящая не только от переменной x, но и от одной произвольной постоянной С такая, что:
, зависящая не только от переменной x, но и от одной произвольной постоянной С такая, что:
А) она удовлетворяет уравнению при любом значении С.
б) каково бы ни было начальное условие 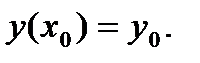 можно найти единственное
можно найти единственное  , что функция
, что функция 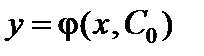 удовлетворяет данному начальному условию.
удовлетворяет данному начальному условию.
Частным решением называется любая функция 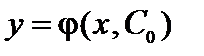 , которая получается из общего решения
, которая получается из общего решения 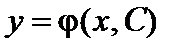 , если произвольной постоянной придать значение
, если произвольной постоянной придать значение 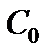 .
.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального уравнения:  Найти особое решение, если оно существует.
Найти особое решение, если оно существует.
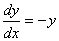
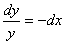
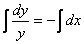
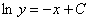
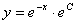
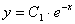
Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1 = eC ¹ 0.
