Пусть мы ищем решение задачи.
ОПТИМИЗАЦИЯ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
Динамическое программирование
Система наблюдается в моментах времени 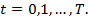
Состояние системы характеризуется числом 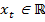 . Известно значение
. Известно значение 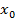 . Система меняет своё состояние под воздействием управлений
. Система меняет своё состояние под воздействием управлений 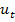 , которые можно свободно выбирать из заданного множества
, которые можно свободно выбирать из заданного множества 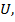 которое назовём областью управления.Управления влияют на состояния системы по правилу
которое назовём областью управления.Управления влияют на состояния системы по правилу
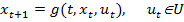 , (1)
, (1)
где 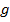 – заданная функция.
– заданная функция.
Предположим, что выбраны величины 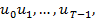 . Тогда, начиная с
. Тогда, начиная с 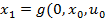 ), далее получим
), далее получим 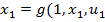 ) и т.д.
) и т.д.
Таким образом, каждому выбору управлений соответствует свой путь (или график).
Пусть имеется функция 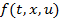 такая, что польза от выбранного пути есть сумма:
такая, что польза от выбранного пути есть сумма:
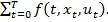 (*)
(*)
Эта сумма носит название целевой функции.
Иногда вместо 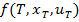 пишут
пишут 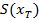 .
.
Вместе с любой заданной последовательностью 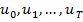 находим последовательность
находим последовательность 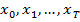 и получаем соответствующие допустимые пары. При этом целевая функция принимает определенное значение.
и получаем соответствующие допустимые пары. При этом целевая функция принимает определенное значение.
Задача состоит в том, чтобы среди всех наборов допустимых пар 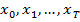 и
и 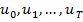 найти оптимальный набор пар
найти оптимальный набор пар 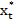 ,
, 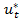 , дающий наибольшее значение целевой функции.
, дающий наибольшее значение целевой функции.
Задача, в краткой формулировке, записывается так:
найти
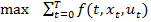 при условиях
при условиях 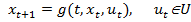 ,
, 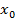 задано, (2).
задано, (2).
Рассмотрим пример реальной задачи, которая решается по изложенной выше схеме.
Пусть 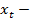 средства в момент
средства в момент 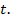 В каждый момент
В каждый момент 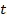 пусть
пусть 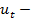 часть, используемая для потребления,
часть, используемая для потребления, 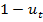 – часть для сбережения. Средства можно употребить в дело с уровнем прироста
– часть для сбережения. Средства можно употребить в дело с уровнем прироста 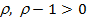 . После изъятия количества средств
. После изъятия количества средств 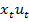 , остаток средств
, остаток средств 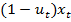 идёт в дело. При этом, с учётом прироста, получаем
идёт в дело. При этом, с учётом прироста, получаем 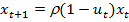 .
.
Пусть польза от потребления 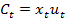 равна
равна 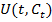 .
.
Пусть функция 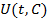 возрастает и выпукла вверх по
возрастает и выпукла вверх по 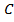 .
.
Вся полученная польза равна:
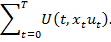
Итак, решается задача:
Найти 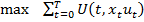 при условиях
при условиях
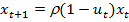
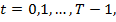
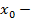 задано,
задано, 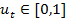 ,
, 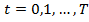 .
.
Свойства целевой функции.
Пусть при 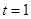 система имеет значение x. Наилучшее, что можно сделать в оставшийся период – выбрать
система имеет значение x. Наилучшее, что можно сделать в оставшийся период – выбрать 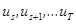 (следовательно,
(следовательно, 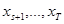 ) так, чтобы максимизировать
) так, чтобы максимизировать 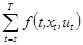 при
при 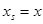 .
.
Назовем оптимальной целевой функцией для этой задачи в момент s.
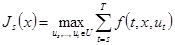 (3)
(3)
где 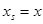 ,
, 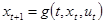 ,
, 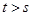 ,
, 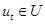 (4)
(4)
Управления, максимизирующие (3) при условиях (4), зависят от х. В частности, 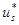 зависит от х.
зависит от х.
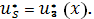 Управления, зависящие от состояния системы назовем политиками.
Управления, зависящие от состояния системы назовем политиками.
Если мы напишем для каждого 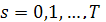 политику, то мы тем самым решили задачу (2)
политику, то мы тем самым решили задачу (2)
Рассмотрим важное свойство целевой функции. При 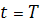 имеем
имеем
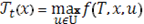 .
.
Пусть при  система в состоянии
система в состоянии 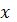 . При выборе
. При выборе 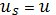 при
при 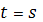 получен выигрыш
получен выигрыш 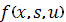 , при этом система окажется в состоянии
, при этом система окажется в состоянии 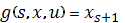
При этом наибольший полный выигрыш, который можно получить от 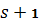 до
до 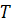 , начиная с состояния
, начиная с состояния 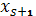 , равен
, равен 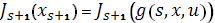
Следовательно, наилучшим выбором для 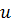 будет то, которое максимизирует сумму
будет то, которое максимизирует сумму 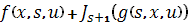
Теорема: Пусть 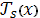 обозначает целевую функцию в момент
обозначает целевую функцию в момент 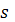
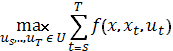
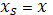 ,
, 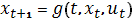 ,
, 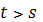
для задачи найти:
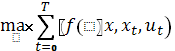 | (5) |
при условиях 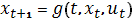 ,
, 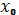 – задано,
– задано, 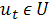
Тогда 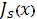 удовлетворяет уравнениям
удовлетворяет уравнениям
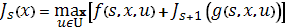 | (6) |
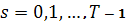
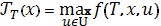 | (7) |
Замечание: Разумеется значения 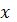 выбираются среди решений разностного уравнения (1) при фиксированном
выбираются среди решений разностного уравнения (1) при фиксированном 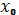 и возможных выборах
и возможных выборах 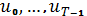 .
.
Обычно эта теорема используется так: ищем функцию (7).
Максимизируются значение U*T (x). Следующий шаг – используя (6) найти JT-1(x) и соответствующую W*T-1(x). Действуя аналогично, находим все JT (x), JT-1(x),….,J0(x) и соответствующие U*T(x), U*T-1(x),…,U*0(x).
Это позволяет построить решение исходной задачи оптимизации.
Пример.
Рассмотрим задачу найти:
max 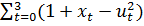 , при условиях
, при условиях 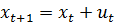 , t=0, 1, 2,
, t=0, 1, 2, 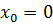 ,
, 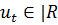 .
.
Здесь T=3, f(t,x,u)=1+x-u2 , g(t,x,u)=x+u.
Из (7) при T=3получаем, что J3(x) представляет собой наибольшее значение функции 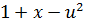 ,
, 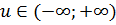 .
.
Оно получается при u=0, т.е. J3(x)=1+x, 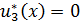 .
.
При s=2 функция максимизируется, обозначим ее h2(u)=1+x-u2+J3(x+u)
Так как J3(x)=1+x, J3(x+u)=1+(x+u) и h2(u)=1+x-u2+1+x+u=2+2x+u-u2; h2’(u)=1-2u, h2’(u)=0, u=1/2, h2(u) выпукла вверх, то u, u2*(x)=1/2, J2(x)=h2(u2*(x))=2+2x+1/2-1/4=2x+9/4.
При s=1 мы максимизирует функцию h1(u)=1+x-u2+2(x+u)+9/4=3x+2u-u2+13/4
h1’(u)=2-2u; h1’(u)=0, u=1.
Находим u1*(x)=1 и J1(x)=3x+2-1+13/4=3x+17/4.
При s=0 максимизируется функция
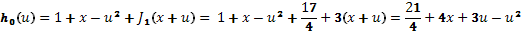 .
. 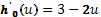
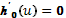
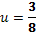
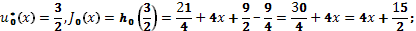
Укажем оптимальные значения состояния системы:
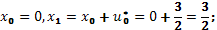
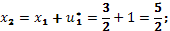
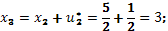
Оптимальное значение целевой функции:
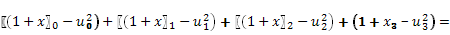
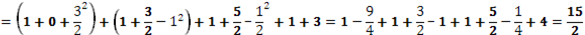 .
.
В простых случаях, подобных рассмотренному, задача динамической оптимизации допускает решение с использованием обычных методов анализа.
Полагая в уравнении
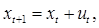
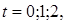
последовательно получаем
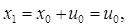
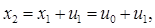
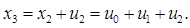
Таким образом, максимизация целевой функции равна
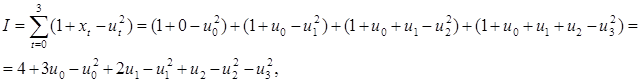
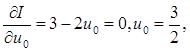
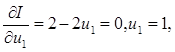
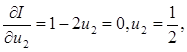
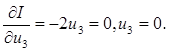
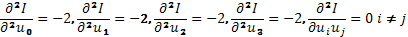
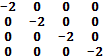 - матрица 2 дифференциала
- матрица 2 дифференциала
По критерию Сильвестра второй дифференциал – отрицательно определенная форма следовательно получаем тоже максимум
Подобный подход возможен в любой задаче, но он слабо реализуем при больших T.
Рассмотрим еще одну задачу :
Найти
max 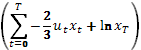
при условии 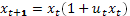
Поскольку 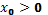 и
и
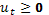 для
для 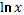 t выполняется неравенство
t выполняется неравенство 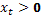
Далее , 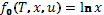 независимо от u , и поэтому
независимо от u , и поэтому 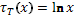 и любое решение
и любое решение 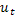 оптимальнее
оптимальнее
Уравнение (1) при S=T-1 дает 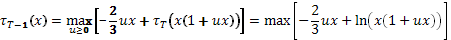
Первая производная по u функции 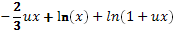 равна
равна
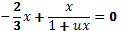 ,
,
1+ux=3/2, ux=1/2.
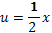
При этом 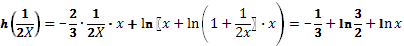 .
.
Итак, 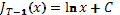 (
( 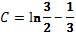 )
)
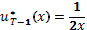
Рассмотрим уравнение (6) при 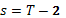
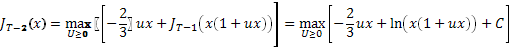
Снова получаем
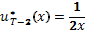 ,
,
при этом 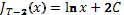
Очевидно, что далее, продолжая процесс, получим
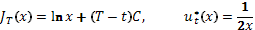
Подстановка 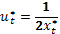 в разностное уравнение дает
в разностное уравнение дает 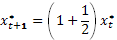 =
= 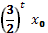
При этом 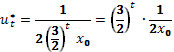 .
.
Примечание
Теорема справедлива и в том случае, когда область управления не фиксирована, но зависит от 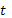 и
и 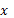 ,
, 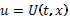 . Тогда максимизация в (2), (3), (5) выполняется при
. Тогда максимизация в (2), (3), (5) выполняется при 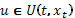 . В (6)(стр. 7),(7)(стр. 7) максимизациявыполняется при
. В (6)(стр. 7),(7)(стр. 7) максимизациявыполняется при 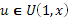 и
и 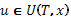 , соответственно.
, соответственно.
Часть множеств 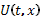 задается набором неравенств
задается набором неравенств 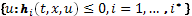 .
.
Если 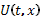 - пустое множество, то принимается соглашение, по которому максимум взят по этому множеству равен -
- пустое множество, то принимается соглашение, по которому максимум взят по этому множеству равен - 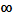 .
.
Рассмотрим задачу, в которой
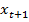 =
= 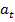 (
( 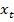 -
- 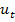 ),
), 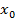 > 0,
> 0, 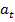 - заданные положительные числа
- заданные положительные числа
β = 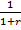 , r – уровень дисконтирования, 0 <
, r – уровень дисконтирования, 0 < 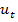 <
< 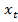 , γ
, γ 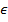 (0, 1), A>0
(0, 1), A>0
Ищется
max ( 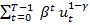 +
+ 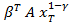 ) (I)
) (I)
В соответствии со сделанным замечанием, 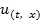 = (0, x)
= (0, x)
f(t, x, u) = 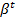
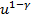 , t = 0, 1, … T-1
, t = 0, 1, … T-1
f(T, x, u) = 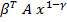 - эта функция от u не зависит, и ее максимум, равный
- эта функция от u не зависит, и ее максимум, равный 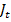 совпадает с ней самой,
совпадает с ней самой, 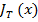 =
= 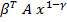 (II), и любое
(II), и любое 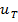 = (0, x) – оптимальное.
= (0, x) – оптимальное.
Из (6) получаем
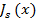 =
= 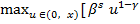 +
+ 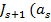 (x-u))] (III)
(x-u))] (III)
При s = T-1
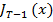 =
= 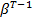
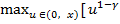 +
+ 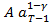
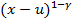 ] (IV),
] (IV),
так как
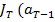 (x-u)) =
(x-u)) = 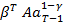
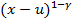
Для 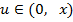 обозначим
обозначим
g(u) = 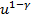 +
+ 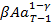
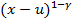
Тогда g’(u) = (1-γ) 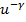 + (1-γ)(-1)
+ (1-γ)(-1) 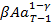
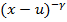
g’(u) =0 ó 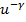 = (-1)
= (-1) 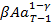
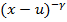
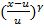 =
= 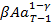
 = 1 +
= 1 + 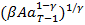 =
= 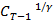 (V)
(V)
u = 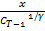
так как g’(u) = (1-γ)(-γ) 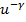 + (1-γ)(-γ)
+ (1-γ)(-γ) 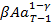
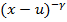 ,
, 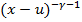 < 0,
< 0,
поэтому 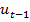 максимизирует g(u)
максимизирует g(u)
g ( 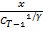 ) =
) = 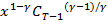 + β A
+ β A 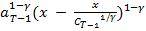 =
=
= 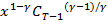 +
+ 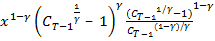 =
= 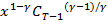 (1 + β A
(1 + β A 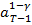 (
( 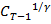 -1)) =
-1)) =
β A 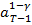 =
= 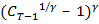
= 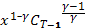 (1 +
(1 + 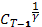 -1) =
-1) = 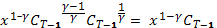 (VI)
(VI)
Тогда ввиду (IV), (VI) (в (VI) вычитаем max y(u), подставляем в (IV))
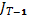 (x) =
(x) = 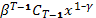
Отметим, что 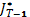 имеет тот же вид, что и
имеет тот же вид, что и 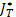
Для s= T-2
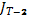 (x) =
(x) = 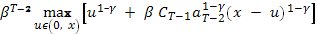
По аналогии со сделанным выше находим, что максимум достигается при 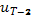 = u =
= u = 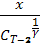 , где
, где 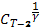 = 1+
= 1+ 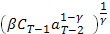 и где
и где 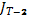 (x) =
(x) = 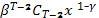
Продолжая аналогично, находим для любого t
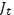 (x) =
(x) = 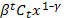 , где
, где 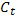 = A, а для
= A, а для 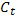 при t<T имеем
при t<T имеем
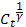 = 1+
= 1+ 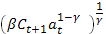 = 1 +
= 1 + 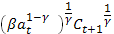
Оптимальное управление:
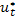 (x) =
(x) = 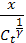 , t<T
, t<T
Для нахождения оптимальных 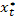 подставляем эти значения в рекурсивное уравнение
подставляем эти значения в рекурсивное уравнение
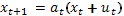
Предположим что для всех t тогда
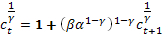
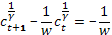
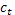 линейное уравнение первого порядка с постоянным коэффициентом
линейное уравнение первого порядка с постоянным коэффициентом
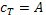
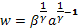
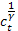 =
= 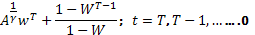
См раздел 14 страница 1 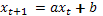
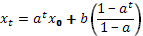
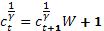
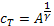
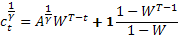
Уравнение Эйлера
Рассмотри задачу найти 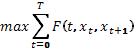 (1) при заданном значении
(1) при заданном значении 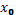 и свободно изменяющихся
и свободно изменяющихся 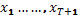
С другой стороны часто можно переформулировать задачу динамического программирования в виде (1)
Если положить 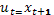 получим задачу с U=R
получим задачу с U=R
Предположим что уравнение 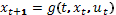 при любом выборе
при любом выборе 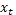 и
и 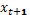 имеет единственное решение
имеет единственное решение 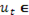 U
U
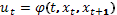
Определим f( 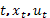 )=f(t, xt,
)=f(t, xt,  )=
)= 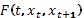 при
при
t<T и 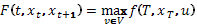 .
.
Иными словами,
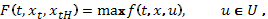
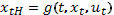
Пусть 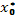 , … ,
, … , 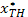 - оптимальное решение задачи (1). Для любого заданного t производная выражения (1) по
- оптимальное решение задачи (1). Для любого заданного t производная выражения (1) по 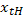 равна 0. Положим
равна 0. Положим 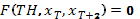 , тогда
, тогда 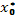 , … ,
, … , 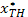 удовлетворяют уравнению Эйлера:
удовлетворяют уравнению Эйлера:


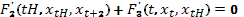 (2)
(2)
|
Это разностное уравнение второго порядка, подобное уравнению Эйлера из вариационного исчисления.
При t = T уравнение (2) переходит в 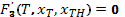 , из которого находим
, из которого находим
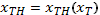
Эта величина подставляется в (2) при t = T-1 и получаем 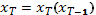 и т.д., так не получим
и т.д., так не получим 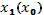 , а
, а 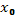 задано
задано
Рассмотрим задачу
найти
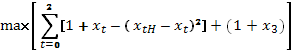 ,
,
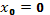 ,
, 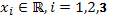
Положим, для t=0,1,2
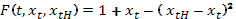
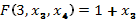 при t=0,1,2
при t=0,1,2
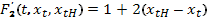
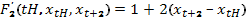
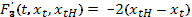
Поэтому уравнение Эйлера при t=0,1 принимает вид
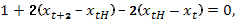
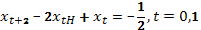
При t=2 уравнение Эйлера имеет вид
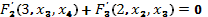 ,
,
так как 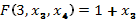
Построим
 ,
,
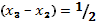 .
.
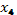 не участвует в построении уравнения Эйлера:
не участвует в построении уравнения Эйлера: 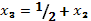 .
.
При 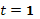
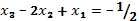 и
и
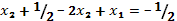 ,
,
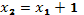 .
.
Подставим в 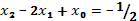 , учтем, что
, учтем, что 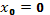 ,
,
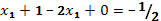 ,
,
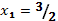 ;
;
Тогда 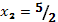 ,
, 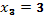 .
.
Свести к задаче динамического программирования можно так:
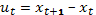 ,
, 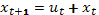 ;
;
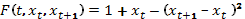 ,
, 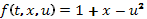
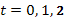 ,
,
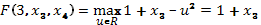 .
.
Infinite Horizon
Неограниченный период.
Проблема ставится так:
найти 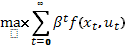 (1)
(1)
при условии, что 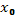 - заданное число,
- заданное число,
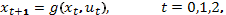 …
…
 .
.
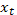 ,
,  – допустимая пара последовательностей, если
– допустимая пара последовательностей, если 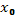 - задано,
- задано, 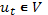 ,
, 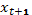 определяется уравнением
определяется уравнением 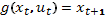 . При этом
. При этом 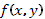 , g
, g 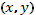 не зависят от переменной t явно. Таким образом (1) называется автономным рядом.
не зависят от переменной t явно. Таким образом (1) называется автономным рядом.
f удовлетворяет условиям ограниченности 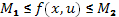 для всех x,u, u
для всех x,u, u 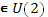 . Поэтому ряд в (1) сходится. Сравним с прогрессией.
. Поэтому ряд в (1) сходится. Сравним с прогрессией.
Пусть π̅ = (us , us+1 , …) – последовательность управлений, гдеus+kϵU, k = 0, 1, … ;xt+1 = g(xt , ut), t = s, s+1, … ; xs = x.
Тогда польза, полученная за период t = s, s+1, … равна
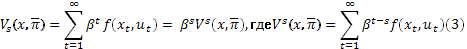
Положим, что
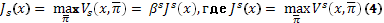
и максимумы взяты по всем последовательностям π̅.
Таким образом, 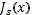 – максимальный успех, который можно получить от t=s до +∞.
– максимальный успех, который можно получить от t=s до +∞.
При условии, что в момент t=s система находится в состоянии x, 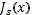 называется оптимальной целевой функцией для задачи (1).
называется оптимальной целевой функцией для задачи (1).
Имеем 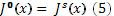
Максимизируя 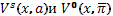 получаем одно и то же значение в обоих случаях, поскольку будущее (+∞) выглядит вполне одинаково в момент 0 и в момент s.
получаем одно и то же значение в обоих случаях, поскольку будущее (+∞) выглядит вполне одинаково в момент 0 и в момент s.
Из (5) следует: 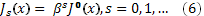
Положим, по определению 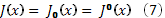
Из (6) следует, что если мы знаем 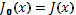 , то мы знаем
, то мы знаем 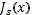 для всех s.
для всех s.
Теорема. Целевая функция 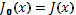 в (4) для задачи (1) удовлетворяет уравнению Беллмана.
в (4) для задачи (1) удовлетворяет уравнению Беллмана.
J (x) = max [f(x,u)+ßJ(g(x,u))] (8)
uÎU
Грубое рассуждение напоминает рассуждения для конечного периода Т. Предположим, что мы при t=0 находимся в состоянии х. Выбрав управление u, получаем βо f(x,u)=f(x,u) и во время t=1 попадаем в x1=g(x,u).
Выбор оптимальной последовательности управлений при t=1 и так далее даёт прибавку в последующий период J1(g(x,u))=βJ(g(x,u)). Следовательно, наилучший выбор при t=0, тот что максимизирует сумму f(x,u) +βJ(g(x,u)), поэтому максимум этой суммы равен J(x)
(8) – функциональное уравнение, можно доказать, что при условиях ограниченности (2), и полагая, что максимум в правой части (8) существует, это уравнение имеет единственное решение которое автоматически является оптимальным уравнением u(x), максимизирующее правую часть (8) — оптимальное и оно не зависит от t. Обычно решить уравнение (8) бывает непросто.
Пусть мы ищем решение задачи.
Найти
∞
Max∑ βt(xt, vt)1- ɣ (1)
xt+1=a(1-v1)xt, t=0,1....
VtÎ(0,1)
a>0, x0>0, βÎ (0,1), ɣÎ (0,1)
β a1- ɣ <1
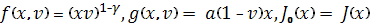 , уравнение (8) имеет вид
, уравнение (8) имеет вид
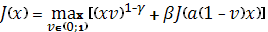 (ii)
(ii)
Задача напоминает задачу, в которой целевая функция была пропорциональна 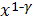 . Предположим, что и в этой похожей задаче
. Предположим, что и в этой похожей задаче 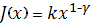 при некоторой постоянной k.
при некоторой постоянной k.
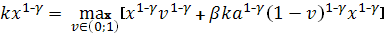
Или, сокращая на 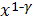 > 0:
> 0:
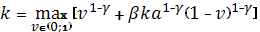 (iii)
(iii)
Положим 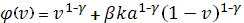 .
.
Тогда 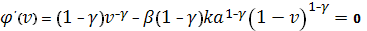
или 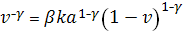
или 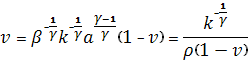 , где
, где 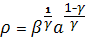
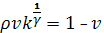
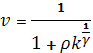 (IV)
(IV)
Так как ϕ’’(ϑ)<0, и так как ϑϵ(0;1).
Таким образом, в предположении, что
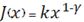
найдено максимизирующее управление (iv).
При этом из (iii)следует, что
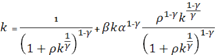 ,
,
Так как 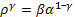 , получаем
, получаем
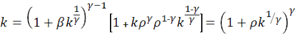
Или 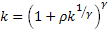
Откуда
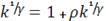
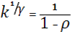
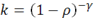
Тогда (iv): 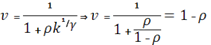
В итоге получаем:
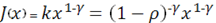
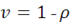
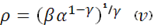
В этом примере, однако
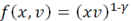
И условия ограниченности не выполнены.
Поэтому следует слегка изменить задачу, положив 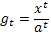
Тогда 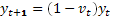
В новой задаче целевая функция равна
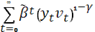 ~
~
Где 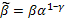 , откуда 0< β<1.
, откуда 0< β<1.
Легко видеть, что 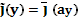 удовлетворяет уравнению Беллмана для новой задачи (с тем же оптимальным значением
удовлетворяет уравнению Беллмана для новой задачи (с тем же оптимальным значением 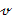 ).
).
Условие ограниченности выполнено, т.к.
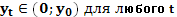
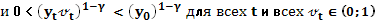
Таким образом 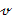 в (IV) оптимальное.
в (IV) оптимальное.
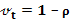 , соответствующее xz удовлетворяет уравнению
, соответствующее xz удовлетворяет уравнению
xt+1 = a(1-ut) xt = a(1-u)xu=ar xt
При условии 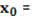 решением является xt = x(ar )t
решением является xt = x(ar )t
Значение функции
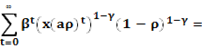
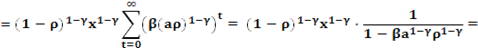
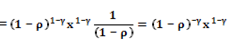
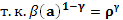
И мы проверим, что значение целевой функции есть в такой 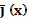 в (V)
в (V)
Важный вопрос, а существует ли искомые максимумы?
Если выполнены (2), ФУНКЦИИ f,g непрерывны и U компактна, то максимумы в (4) и(8) существует. Кроме этого, (8) имеет единственное решение, если использовать теорему о сжимающем отображении.
Принцип максимума
Мы рассматривали метод динамического программирования. Другой метод основан на принципе максимума. Этот метод удобен, когда есть ограничения на разовую пере6менную.
Рассмотрим задачу найти
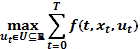 ,
,
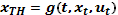 , t=0,…,T-1 (1)
, t=0,…,T-1 (1)
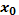 – задано,
– задано, 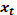 – свободно
– свободно
Пусть U представляет собой интервал
Определим функцию Понтрягина (Hamiltonian)
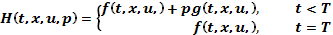 (2)
(2)
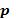 – сопряжения (присоединения) функции
– сопряжения (присоединения) функции
