Флажок итоговая статистика

Уровень надежности: равносильно доверительной вероятности g=0,95 или уровню значимости a= 0,05.

4). По результатам графиков распределений (гистограмм) и числовых характеристик (таблица описательной статистики) можно выдвинуть гипотезу о наличии связи между переменными и характере этой связи; для изучения технологии регрессионного анализа выдвигаем гипотезу о наличии между переменными линейной зависимости.

Этап 3. Оценивание параметров зависимости

1). Находясь на рабочем листе Исходные данные, выполняем команду

Анализ данных®Регрессия;

2). Заполняем параметры диалогового окна Регрессия

Входные данные

Входной интервал Y – вводятся ссылки на ячейки, содержащие данные по показателю; диапазон должен состоять из одного столбца ( e2:e81)

Входной интервал Х - вводятся ссылки на ячейки, содержащие значения факторов. (c2:c81). Максимальное число входных диапазона (столбцов) равно 16.

Метки устанавливается в активное состояние, если первая строка (столбец) во входном диапазоне содержит заголовки. Если заголовки отсутствуют, флажок следует снять. В этом случае будут автоматически созданы стандартные названия.

Уровень надежности (по умолчанию 95%). Установленный уровень надежности используется для проверки значимости коэффициента детерминации R² и коэффициентов регрессии.

Константа-ноль. Флажокустанавливается, если требуется, чтобы линия регрессии прошла через начало координат (т.е. b=0)

Параметры вывода

Выходной интервал/Новый рабочий лист/Новая рабочая книга

Остатки и Стандартизированные остатки устанавливаются, если требуется включить в выходные данные столбец остатков или столбецстандартизированных остатков

График остатков устанавливается, если требуется вывести на рабочий лист точечные графики зависимости остатков от факторов.

График подбора устанавливается, если требуется вывести на рабочий лист точечные графики зависимости теоретических значений показателя от факторов.

График нормальной вероятности устанавливается, если требуется вывести на рабочий лист точечный график зависимости наблюдаемых значений y от автоматически формируемых интервалов персентилей.

3). После нажатия кнопки ОКна отдельном листе получаем результаты регрессионного анализа.

ВЫВОД ИТОГОВ
Т1
Регрессионная статистика
Множественный R	0,698168
R-квадрат	0,487438
Нормированный R-квадрат	0,458962
Стандартная ошибка	2,36666
Наблюдения
Т2
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		95,87757	95,87757	17,1177	0,000619
Остаток		100,8194	5,601079
Итого		196,697
Т3
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	3,76939	0,533002	7,071996	1,35E-06	2,649594	4,889187	2,649594	4,889187
X(Н:0;1)	2,251956	0,544299	4,137354	0,000619	1,108427	3,395485	1,108427	3,395485

Этап 4. Проверка адекватности построенной модели

С этой целью проводят дисперсионный и корреляционный анализ полученной зависимости. За нас эту работу продел Excel, нам остается только проинтерпретировать полученные результаты и сделать выводы о качестве построенной модели.

Дисперсионный анализ(2 –я таблица)

	df	SS	MS	F
Регрессия	dfр=1	SSр=	MSр= SSр/dfр
Остаток	dfoc=n-2	SSoc=	MSoc= SSoc/ dfoc
Итого	Dfср=n-1	SSср=	MSср= SSср/ dfср

Обозначения:

- сумма квадратов отклонений;

- число степеней свободы;

- средний квадрат (оценка дисперсии);

- сумма квадратов отклонений относительно общего среднего;

- сумма квадратов отклонений относительно линии регрессии (ошибка);

-сумма квадратов отклонений, связанная с регрессией.

Всякая сумма квадратов связана с числом степеней свободы. В статистике числом степеней свободы некоторой величины часто называют разность между числом различных опытов и числом констант, найденных по этим опытам независимо друг от друга. Например, для образования (относительно среднего) требуется (n-1) независимый элемент, т.к. из чисел , ,…, независимы только n-1, поскольку среднее – линейная комбинация, то число степеней свободы равно разности между числом наблюдений n и числом оцениваемых параметров. Þ число ст. свободы = число наблюдений – число оцениваемых параметров. SS_р – имеет одну степень свободы.

Проверка гипотезы линейной связи состоит в расчленении суммы квадратов отклонений от общего среднего на 2 составляющие.

Основное дисперсионное тождество:

= + , где

- сумма квадратов отклонений относительно общего среднего;

- сумма квадратов отклонений относительно линии регрессии (ошибка);

-сумма квадратов отклонений, связанная с регрессией

Т.о. разброс Y – ков относительно среднего можно приписать тому факту, что не все действительные наблюдения лежат на линии регрессии. Пригодность уравнения регрессии для целей прогнозирования зависит от того, какая часть суммы квадратов отклонений относительно среднего приходится на сумму квадратов, обусловленную регрессией, и какая часть соответствует сумме квадратов относительно регрессии, т.е. является ошибкой.

Уравнение регрессии считают удовлетворительным, если SS_р будет много больше, чем SS_oc (относительно регрессии). Или отношение будет не слишком сильно

Вывод 1 (предварительный):

если SS_р>> SS_oc ,то уравнение регрессии хорошо отражает зависимость между переменными (адекватно);

если SS_р< SS_oc ,то уравнение регрессии не отражает зависимость в исходных данных (неадекватно);

Для оценки адекватности уравнения регрессии дисперсия, обусловленная регрессией (MS_р) сравнивается с остаточной дисперсией (MS_ос), для чего используется F-статистика (F-распределение), так называемый критерий Фишера – отношение средних квадратов:

F_p= , где MS_р - дисперсия, обусловленная регрессией.

MS_ос – остаточная дисперсия относительно регрессии;

В таблице F-распределения находят табличное значение критерия Фишера - F_T с числом степеней свободы числителя n₁ (df_p) и знаменателя n₂ (df_ос).

Вывод 2 (окончательный):

если F>F_т, то уравнение регрессии адекватно исходным данным (основная часть вариации связана не с остатками, а с перемещением по линии регрессии);

если F<F_т, то уравнение регрессии неадекватно исходным данным и предположение о линейной зависимости неверно. В этом случае адекватную зависимость между переменными следует искать в другом классе функций.

Корреляционный анализ(1 –я таблица)

Регрессионная статистика

Множественный R	R=
R-квадрат	R2=
Нормированный R-квадрат
Стандартная ошибка
Наблюдения	n

Исследует степень связи между случайными величинами, для этого используются величины:

R² – коэффициент детерминации, характеризует меру качества подбора зависимости

, определяет долю дисперсии, объясненной регрессией (SS_p) в общей дисперсии зависимой переменной (SS_cp).

R - коэффициент корреляции, является мерой линейной связи между переменными. Оценку значения коэффициента корреляции находят по формуле:

R =

Множественный коэффициент корреляции характеризует степень линейной взаимосвязи между переменными Y и 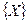. Чем теснее данные примыкают к линии регрессии, тем выше значение этого показателя.

Из формулы видно, чем ближе значение R² к 1, тем ближе суммарная ошибка SS_oc= приближается к 0.

Свойства коэффициента детерминации (R²):

1.Значение R=1 соответствует функциональной линейной связи, т.е. все исходные значения лежат на линии регрессии.

2. R=0 или @ 0 означает, что линейной связи нет.

3. 0.3< R £ 0.5 – слабая линейная связь

0.5 < R £ 0.7 - средняя линейная связь

R > 0.7 - сильная линейная связь

Вывод 3 Степень связи между переменными.

Подведем итог проделанной работе:

1 Поставлена однофакторная задача регрессионного анализа;

2 С помощью инструмента генерации случайных чисел получены исходные экспериментальные данные;

3 Выдвинута гипотеза о существовании линейной связи между переменными Х и Y;

4 Средствами Excel на основе экспериментальных данных найдены коэффициенты регрессии a и b (МНК).

В дальнейшем на основе построенной регрессионной зависимости возможно ставить и решать например, следующие задачи:

- управление качеством продукции;

- оптимизация входных параметров технологического процесса;

- прогноз и анализ объемов произведенной продукции и другие.

Как правило, стараются выбрать простой класс функций (константы, линейные, кусочно-линейные). Чаще всего поиск ММ ведут в классе линейных функций. Это обусловлено следующими причинами:

- качество экспериментального материала (ошибки измерения);

- отсутствие априорной информации о виде ММ;

- существование хорошо проработанных численных процедур оценивания коэффициентов линейных моделей;

- интерпретируемость результатов.

Алгоритм регрессионного анализа