Сызықтық байланысты және сызықтық байланыссыз
Векторлар жүйелері
n  1. Сызықтық байланысты (СБ) және сызықтық байланыссыз (СБ-сыз)
1. Сызықтық байланысты (СБ) және сызықтық байланыссыз (СБ-сыз)
векторлар жүйелерінің анықтамасы, мысалдары
Айталық, V= 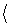 V, +,
V, +, 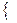

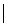
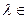 F
F 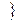
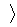 – F өрісінде берілген векторлық кеңістік, ал а
– F өрісінде берілген векторлық кеңістік, ал а  , а
, а  , ... , а
, ... , а 
 V (1) векторлар жүйесі болсын.
V (1) векторлар жүйесі болсын.
Анықтама. Егер скалярлар өрісінен бәрі бірдей нольге тең болмайтын  ,
, 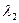 ,...,
,..., 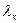 скалярлары табылып,
скалярлары табылып,  а
а  +
+ 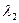 а
а  + ... +
+ ... + 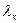 а
а  векторы нольдік вектор болса, онда (1) векторлар жүйесін сызықтық байланысты (СБ) дейді.
векторы нольдік вектор болса, онда (1) векторлар жүйесін сызықтық байланысты (СБ) дейді.
def
( (1) – СБ)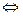 (
( 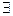
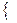
 ,
, 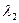 ,...,
,..., 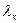
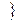
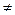
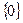
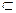 F
F  а
а  +
+ 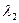 а
а  + ... +
+ ... + 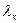 а
а  = 0)
= 0)
СБ ұғымы жазықтықта коллинеар, кеңістікте компланар ұғымдарын береді.
Анықтама. Егер (1) векторлар жүйесінің  а
а  +
+ 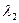 а
а  + ... +
+ ... + 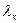 а
а  сызықтық комбинациясы тек
сызықтық комбинациясы тек  ,
, 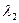 ,...,
,..., 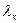 скалярларының бәрі ноль болғанда ғана нольдік векторға тең болса, онда ол жүйені СБ-сыз дейді.
скалярларының бәрі ноль болғанда ғана нольдік векторға тең болса, онда ол жүйені СБ-сыз дейді.
def
((1)–СБ-сыз)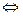 (
(
 ,
, 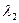 ,...,
,..., 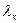
 F (
F (  а
а  +
+ 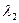 а
а  + ... +
+ ... + 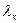 а
а  = 0
= 0 
 =...=
=...= 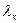 = 0 ))
= 0 ))
Мысалдар.
1). F 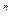 – n өлшемді арифметикалық векторлық кеңістіктің а
– n өлшемді арифметикалық векторлық кеңістіктің а  = (
= ( 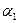 ,0,...,0),
,0,...,0),
а  = (0,
= (0, 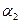 ,...,0),
,...,0),
...................... ,
а  = (0,0,...,
= (0,0,..., 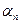 )
)
векторлары СБ-сыз жүйе болады. Жеке жағдайы, R 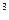 кеңістігінде а
кеңістігінде а  = (3,0,0),
= (3,0,0),
а  = (0,-5,0),
= (0,-5,0),
а 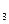 = (0,0,
= (0,0, 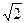 )
)
векторларының жүйесі СБ-сыз. Бұл кеңістікте (1,0,0),
(0,1,0),
(0,0,1) векторларының жүйесі де СБ-сыз екені түсінікті. Бұлар R 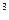 кеңістігінің бірлік векторлары.
кеңістігінің бірлік векторлары.
2). Жазықтықтағы бір О нүктесінен шығатын бағытталған кесінділер кеңістігінің сол О нүктесінен шығатын, өзара перпендикуляр кезкелген екі векторы СБ-сыз жүйе болады.
3). М  (R) – 2-ші ретті квадрат матрицалар кеңістігінде
(R) – 2-ші ретті квадрат матрицалар кеңістігінде
А 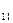 =
= 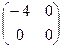 , А
, А  =
= 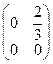 , А
, А  =
= 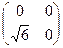 , А
, А  =
= 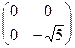
векторлары (матрицалары) СБ-сыз жүйе болады.
n  2. СБ және СБ-сыз векторлар жүйелерінің қасиеттері
2. СБ және СБ-сыз векторлар жүйелерінің қасиеттері
1  . Құрамында нольдік вектор бар жүйе СБ болады.
. Құрамында нольдік вектор бар жүйе СБ болады.
Дәлелдеу. а  , 0, а
, 0, а  , ... , а
, ... , а  векторларының жүйесі берілсін.
векторларының жүйесі берілсін.
F скалярлар өрісінің 0, 
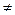 0, 0, ... , 0 элементтері үшін
0, 0, ... , 0 элементтері үшін
0 а  +
+  0+ 0 а
0+ 0 а 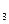 + ... + 0 а
+ ... + 0 а  = 0 д. к. о.
= 0 д. к. о.
2  . Құрамында өзара тең векторлары бар жүйе СБ болады.
. Құрамында өзара тең векторлары бар жүйе СБ болады.
Дәлелдеу. а  , а
, а  , а
, а 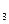 , ... , а
, ... , а  векторларының жүйесі берілсін.
векторларының жүйесі берілсін.
F скалярлар өрісінің 
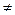 0, –
0, – 
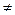 0, 0, ... , 0 элементтері үшін
0, 0, ... , 0 элементтері үшін
 а
а  + (–
+ (–  )а
)а  + 0 а
+ 0 а 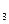 + ... + 0 а
+ ... + 0 а  = 0 д. к. о.
= 0 д. к. о.
3  . Құрамында пропорционал векторлары бар жүйе СБ болады.
. Құрамында пропорционал векторлары бар жүйе СБ болады.
Дәлелдеуі өзбетімен.
4  . Егер векторлар жүйесінің қандайда бір ішкі жүйесі СБ болса, онда жүйенің өзі де СБ болады.
. Егер векторлар жүйесінің қандайда бір ішкі жүйесі СБ болса, онда жүйенің өзі де СБ болады.
Дәлелдеу. а  , а
, а  , ... , а
, ... , а  векторлар жүйесі берілсін.
векторлар жүйесі берілсін.
а  , ... , а
, ... , а 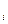 – СБ болсын ( i < к ). Онда СБ-ң анықтамасы бойынша
– СБ болсын ( i < к ). Онда СБ-ң анықтамасы бойынша
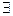
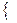
 ,...,
,..., 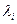
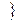
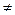
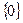
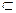 F
F  а
а  + ... +
+ ... + 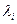 а
а 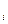 = 0
= 0 

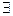
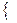
 ,...,
,..., 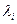 , 0, ..., 0
, 0, ..., 0 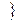
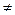
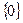
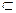 F
F  а
а  + ... +
+ ... + 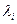 а
а 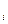 +0а
+0а 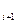 +...+ 0а
+...+ 0а  = 0д.к.о.
= 0д.к.о.
Салдар. Егер векторлар жүйесі СБ-сыз болса, онда оның кезкелген ішкі жүйесі де СБ-сыз болады.
5  . ( Векторлар жүйесінің СБ – лығының критериі )
. ( Векторлар жүйесінің СБ – лығының критериі )
Векторлар жүйесі СБ болу үшін оның бір векторы қалғандарының сызықтық комбинациясы болуы қажет және жеткілікті.
Дәлелдеуі өзбетімен (қара,  1
1  , 2 тарау, §2, 48 бет).
, 2 тарау, §2, 48 бет).
6  . Егер а
. Егер а  , а
, а  , ... , а
, ... , а  векторлар жүйесі СБ-сыз болса, ал а
векторлар жүйесі СБ-сыз болса, ал а  , а
, а  , ... , а
, ... , а  , b
, b
векторлар жүйесі СБ болса, онда b векторы а  , а
, а  , ... , а
, ... , а  жүйесі арқылы сызықтық өрнектеледі.
жүйесі арқылы сызықтық өрнектеледі.
Дәлелдеуі өзбетімен.
7  . Егер b
. Егер b  L(а
L(а  , а
, а  , ... , а
, ... , а  ) және
) және  i =1,2,…,к а
i =1,2,…,к а 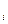
 L(v
L(v  , v
, v  , ... , v
, ... , v 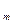 ) болса, онда b
) болса, онда b  L(v
L(v  , v
, v  , ... , v
, ... , v 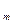 ).
).
(Дәлелсіз қабылдаймыз).
8  . Егер а
. Егер а  , а
, а  , ... , а
, ... , а 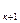
 L(v
L(v  , v
, v  , ... , v
, ... , v  ) болса, онда а
) болса, онда а  , а
, а  , ... , а
, ... , а 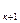 – СБ болады.
– СБ болады.
( Дәлелсіз қабылдаймыз).
Салдар 1. Егер а  , а
, а  , ... , а
, ... , а 
 L(v
L(v  , v
, v  , ... , v
, ... , v 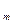 ) және а
) және а  , а
, а  , ... , а
, ... , а  – СБ-сыз болса, онда к
– СБ-сыз болса, онда к 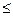 т болады.
т болады.
Бұл салдарды, кейде, векторлық кеңістіктің негізгі теоремасы деп те айтады.
Салдар 2. Егер а  , а
, а  , ... , а
, ... , а 
 L(v
L(v  ,v
,v  , ... ,v
, ... ,v 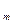 ) және к > m болса, онда а
) және к > m болса, онда а  ,а
,а  , ... ,а
, ... ,а  – СБ болады.
– СБ болады.
Салдар 3. n өлшемді арифметикалық векторлық кеңістікте кезкелген n +1 вектордан (немесе одан да көп вектордан) тұратын жүйе СБ болады.
Мысал.R 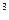 кеңістігінде а
кеңістігінде а  = (2, -3, 1),
= (2, -3, 1),
а  = (3, -1, 5),
= (3, -1, 5),
а 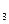 = (1,-4,3) векторларының СБ немесе СБ-сыз болатынын анықтаңыз.
= (1,-4,3) векторларының СБ немесе СБ-сыз болатынын анықтаңыз.
Шығаруы. Анықтама бойынша  а
а  +
+ 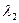 а
а  +
+ 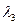 а
а 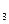 = 0теңдігінен
= 0теңдігінен  – ларды та – бамыз. Бізге
– ларды та – бамыз. Бізге  – лардың бәрі ноль ме, әлде нольден өзгелері табыла ма?, соны анықтау керек. Бізге оларды х – тар арқылы белгілеген қолайлы. Сондықтан
– лардың бәрі ноль ме, әлде нольден өзгелері табыла ма?, соны анықтау керек. Бізге оларды х – тар арқылы белгілеген қолайлы. Сондықтан
х  а
а  + х
+ х  а
а  + х
+ х 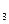 а
а 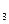 = 0теңдеуін шешеміз.
= 0теңдеуін шешеміз.
(2 х  , -3х
, -3х  , х
, х  ) + (3х
) + (3х  , -х
, -х  , 5х
, 5х  ) + (х
) + (х 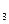 , -4х
, -4х 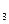 , 3х
, 3х 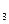 ) = (0, 0, 0)
) = (0, 0, 0)
Кортеждерді қосу ережесінен төмендегідей біртекті СТЖ – сін аламыз:
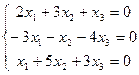
Осы біртекті жүйенің нольдік емес шешулері бар ма, әлде тек нольдік шешу ғана бола ма? Бұл сұраққа жауап беру үшін жүйенің негізгі матрицасының рангсын есептейді. Егер ранг 3-ке тең болса, онда тек нольдік шешу ғана болады; ал ранг 3-тен кіші болса, СТЖ –ң нольдік емес шешулері де болады.
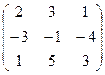 – жүйенің матрицасы. (Берілген векторлармен салыстыр!).
– жүйенің матрицасы. (Берілген векторлармен салыстыр!).
Матрицаның жолдық және бағандық ранглары тең болғандықтан, бұл матрицаның орынына транспонирленген матрицаның рангсын табуға болады.
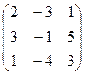 – транспонирленген матрица. (Берілген векторлармен салыстыр!).
– транспонирленген матрица. (Берілген векторлармен салыстыр!).
Сонымен, 3 – өлшемді арифметикалық векторлық кеңістікте берілген векторлар жүйесінің СБ не СБ-сыз болатынын анықтау үшін олардың координаталарынан матрица құрып, оның рангсын есептейміз. Егер ранг 3–ке тең болса, онда векторлар жүйесі СБ-сыз болады; ал ранг 3–тен кіші болса, – СБ болады.
«Сызықтық кеңістіктер» тақырыбына әдебиеттер:
 1
1  . Ильин В.А., Позняк Э.Г., Линейная алгебра, М., 1978
. Ильин В.А., Позняк Э.Г., Линейная алгебра, М., 1978
 2
2  . Куликов Л.Я., Алгебра и теория чисел, М., 1979
. Куликов Л.Я., Алгебра и теория чисел, М., 1979
 3
3  . Ляпин Е.С., Евсеев А.Е., Алгебра и теория чисел (часть 2), М., 1978
. Ляпин Е.С., Евсеев А.Е., Алгебра и теория чисел (часть 2), М., 1978
 4
4  . Мальцев И.А., Линейная алгебра, Санкт-Петербург, 2010
. Мальцев И.А., Линейная алгебра, Санкт-Петербург, 2010
 5
5  . Петрова В.Т., Лекции по алгебре и геометрии (часть 2), М., 1999
. Петрова В.Т., Лекции по алгебре и геометрии (часть 2), М., 1999
 6
6  . Проскуряков И.В., Сборник задач по линейной алгебре , М., 2008
. Проскуряков И.В., Сборник задач по линейной алгебре , М., 2008
 7
7  . Сызықтық алгебра элементтері (методикалық талдау), Құрастырған
. Сызықтық алгебра элементтері (методикалық талдау), Құрастырған
Т.Б.Бұлабаев, А., 1992
