Розділ 5 Метод зверненян до рівняння в скінченних різницях

Нехай розглядається функціональне рівняння виду

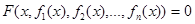, (5.1)

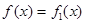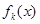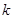де - шукана функція, - її -та ітерація ( 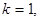2, ..., 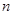). При цьому покладають x=u_t , 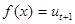. Тут перехід від x до 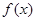здійснюється шляхом заміни t на t+1 у функції u₁. Така заміна дає можливість звести рівняння (5.1) до рівняння в скінчених різницях n–го порядку:

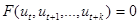
Розв’язок рівняння (5,2) дає вираз для функції u₁ через t і довільні періодичні функції C_k=C_k(t) (k=1, 2, …,n) з періодом, рівним одиниці. Розв’язок функціонального рівняння (5.1) в найбільш загальному вигляді задається такою системою рівнянь:

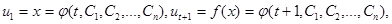(5.3)

де 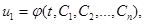- розв’язок рівняння.

Із системи (5.3) випливає, що одержати явний загальний розв’язок рівняння (5.1) в елементарних функціях у загальному вигляді неможливо. Але якщо накласти певні обмеження на 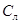, то (5.3) з можна виключити t і отримати частинні розв’язки рівняння (5.1) в явному вигляді.

Приклад 1 Знайти загальний розв’язок функціонального рівняння

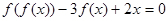(5.4)

і виділити з нього деякі явні частини розв’язків.

Розв’язання: Нехай 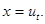. Звідси 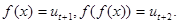Маємо рівняння в скінченних різницях другого порядку.

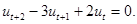
Йому відповідає характеристичне рівняння

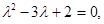
яке має корен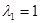і і .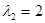

Загальний розв’язок рівняння (5.4) має вигляд:

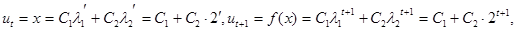(5.5)

де C₁ , C₂ - довільні періодичні функції від змінної t з періодом, рівним одиниці.

Якщо в (5.5) покласти, С₁ і С₂ –довільні сталі, то виключивши t, дістанемо розв’язок 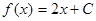, де C=-C- довільна стала. У випадку C₂=0 одержуємо

.

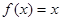Отже, функції 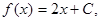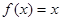задають у явному вигляді розв’язки функціонального рівняння (5.4) .

Висновки

Моя робота складається з 4 основних частин, в яких виложений зміст розвязання функціональних рівнянь. Кожен з них побудований таким чином, що спочатку наводяться короткі теоретичні відомості і зразки розвязань найбільш типових задач. А потім пропонуються вправи для самостійного опрацювання.

Теоретичне підгрунтя перших трьох частин не виходить за межі шкільного курсу математики, тож менібуло дещо легше осмислити і освоїти його. Та останній вимагав позашкільних знань функції, тож написання роботи збагатило мої знання з математики. Також я набула навичок розвязання даних рівнянь у скінченних різницях.

На мою думку доцільно ввести функціональні рівняння в шкільний курс вивчення математики, особливо аналітичний метод і метод підстановок. Адже даний вид рівнянь часто зустрічається на шкільних олімпіадах, конкурсах.

Ввесь же викладенний матеріал можна запропонувати учням старших класів та учителям для факультативних занять, спецкурсв, шкіл олімпіадного резерву, при підготовці до олімпіад, математичних конкурсів і звичайно ж для вступних іспитів у вищі вузи.