Метод наименьших квадратов
Лекции №№ 3 и 4.
Раздел 3. Парная регрессия и корреляция
Линейная парная регрессия: теоретическое и эмпирическое уравнения регрессии; метод наименьших квадратов (МНК); предпосылки МНК; интерпретация уравнения регрессии; оценка значимости коэффициентов регрессии; интервальные оценки коэффициентов линейной регрессии; коэффициенты корреляции, детерминации и эластичности; оценка статистической значимости уравнения регрессии.
Нелинейные модели регрессии и их линеаризация /
Введение
Парной регрессией называется модель, выражающая зависимость среднего значения (условного математического ожидания) зависимой переменной Y от одной независимой переменной X:
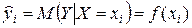или 
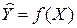
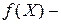функция регрессии.
Парная регрессия применяется, если имеется доминирующий фактор, обуславливающий большую долю изменения изучаемой объясняемой переменной, который и используется в качестве объясняющей переменной.
Различают линейные и нелинейные регрессии. Линейная регрессия: y=a+bx+e. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
· полиномы разных степеней y = a+b1x+b2x2+…+bnxn+e;
· равносторонняя гипербола 
.
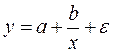Регрессии, нелинейные по оцениваемым параметрам:
· степенная y=a×xb×e;
· показательная y=a×bx×e;
· экспоненциальная y=e a+b×x×e.
1.1. Линейная регрессия: основные понятия
Если функция регрессии линейна, то говорят о линейной регрессии. Модель линейной регрессии (линейное уравнение) является наиболее простым видом зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.
Парная линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием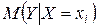 
зависимой переменной Y и одной объясняющей переменной X (xi - значения независимой переменной в i-м наблюдении).
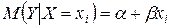(3.1)
Принципиальной является линейность уравнения по параметрам a, β.
Так как каждое индивидуальное значение yi отклоняется от соответствующего условного математического ожидания, в соотношение (3.1) необходимо ввести случайное слагаемое εi ,
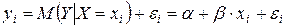(3.2)
Соотношение (3.2) называется теоретической линейной регрессионной моделью, a и β — теоретическими параметрами (теоретическими коэффициентами) регрессии, εi — случайным отклонением.
Отметим, что в эконометрике уравнение и параметры, относящиеся к генеральной совокупности, называют теоретическими.
Уравнение и параметры, полученные в результате оценки с использованием выборочных данных, называют эмпирическими.
Заметим, что обычно преподаватели общей теории статистики эмпирические уравнения называют «теоретическими», а теоретические не рассматривают вовсе.
В общем, теоретическую линейную регрессионную модель будем представлять в виде:
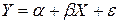(3.3)
Как правило, переменные будем обозначать прописными символами, а индивидуальные значения переменных — соответствующими строчными. Теоретические значения параметров обозначаем буквами греческого алфавита, а их оценки — латинскими.
Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных Y и X генеральной совокупности, что невозможно. Таким образом, задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным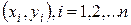 
для переменных X и Y:
а) получить наилучшие оценки неизвестных параметров a и β;
б) проверить статистические гипотезы о параметрах модели;
в) проверить, достаточно ли хорошо модель согласуется со статистическими
данными (адекватность модели данным наблюдений).
Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии:
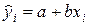(3.4)
где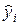 
— оценка условного математического ожидания ;
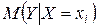a и b — оценки неизвестных параметров a и β, называемые эмпирическими коэффициентами регрессии.
В конкретном случае:
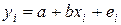(3.5)
где отклонение еi — оценка теоретического случайного отклонения εi.
В силу несовпадения статистической базы для генеральной совокупности и выборки оценки a и b практически всегда отличаются от истинных значений коэффициентов a и β, что приводит к несовпадению эмпирической и теоретической линий регрессии.
Возможное соотношение между теоретическим и эмпирическим уравнениями регрессии схематично изображено на рис.3.1.
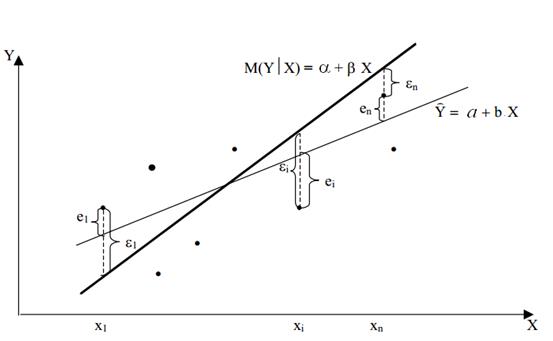
Рис.3.1.
Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок.
Задача состоит в том, чтобы по конкретной выборке 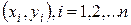найти оценки a и b неизвестных параметров a и β так, чтобы построенная линия регрессии являлась наилучшей в определенном смысле среди всех других прямых линий. Построенная прямая 
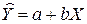должна быть «ближайшей» к точкам наблюдений по их совокупности.
Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется сумма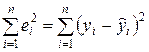 
. Он получил название метод наименьших квадратов (МНК). Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств.
Метод наименьших квадратов
При использовании МНК минимизируется следующая функция:
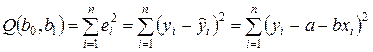(3.6)
Необходимым условием существования минимума функции двух переменных (3.6) является равенство нулю ее частных производных по неизвестным параметрам b0 и b1
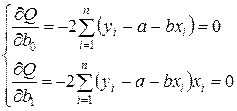(3.7)
После группировки систему можно записать в виде:
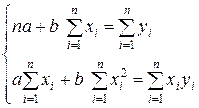(3.8)
Система (3.8) называется системой нормальных уравнений МНК.
Решая систему (3.8) либо методом исключения переменных, либо методом определителей, найдем искомые оценки a и b.
Если все слагаемые в (3.8) разделить на n, то получим систему:
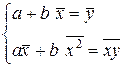(3.9)
Из первого уравнения
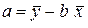(3.10)
Тогда, подставляя (3.10) во второе уравнение систему(3.9), найдем b1:
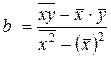(3.11)
Справедливы следующие утверждения:
1. Оценки МНК определяются по выборке (являются функциями выборки).
2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.
3. Согласно первой формуле системы (3.9), эмпирическая прямая регрессии обязательно проходит через точку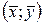 
.
4. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений, а также среднее значение отклонения равнялись нулю: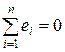 
; 
.
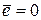5. Остатки еi не коррелированны с наблюдаемыми значениями xi независимой переменной X.
6. Остатки еi не коррелированны со значениями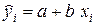 
Пример 3.1. Для анализа зависимости объема потребления Y (ден. ед.) домохозяйства от располагаемого дохода X (ден. ед.) отобрана выборка объема n = 20 домохозяйств, результаты которой приведены в табл. 3.1. Необходимо определить вид зависимости, по МНК оценить параметры уравнения регрессии Y на X и спрогнозировать потребление при доходе X= 160.
Таблица 3.1
| X | ||||||||||||||||||||
| Y |
Решение. Для определения вида зависимости построим корреляционное поле
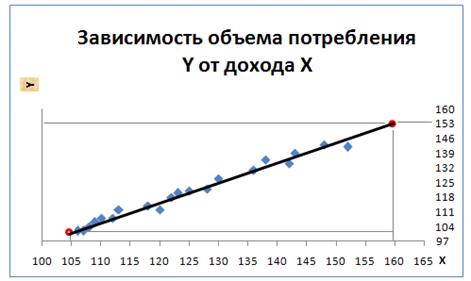
Рис. 3.2.
По расположению точек на корреляционном поле полагаем, что зависимость между X и Y линейная: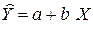 
.
Для определения параметров a и b заполним таблицу 3.2.:
; 
; 
; 
.
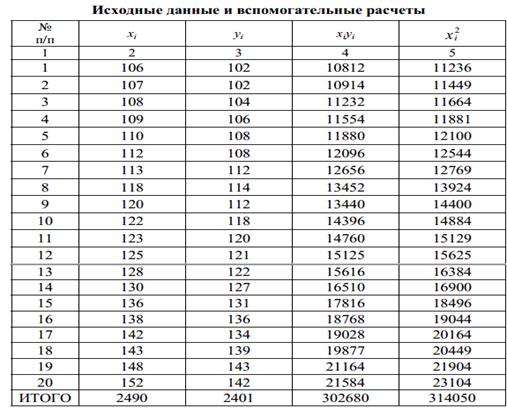
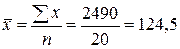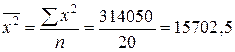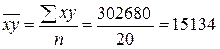По формуле (3.11):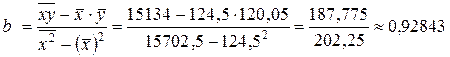 
;
По формуле (3.10):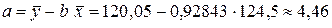 
.
Таким образом, уравнение парной линейной регрессии имеет вид: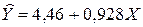 
Данная прямая линия изображена на корреляционном поле. По этому уравнению при xi = 160 рассчитаем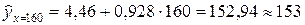 
.