Теорема сложения вероятностей несовместных событий
Т. Вер-сть появл-я 1 из двух несовм. событий, безразлично какого, равна сумме вер-стей этих событий: Р(А + В) = Р А) + Р(В). Док-во: Введем обознач-я: n — общее число возм. элемент. исходов испыт-я; m1 — число исходов, благоприят. событию A; m2— число исходов, благоприят. событию В. Число элемент. исходов, благоприят. наступл-ю либо события А, либо события В, равно m1 + m2. Следовательно, Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n. Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончат. получим Р (А + В) = Р (А) + Р (В). Следствие 1. В-сть появления 1 из нескольких попарно несовм. событий, безразлично какого, равна сумме в-стей этих событий:Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An). С л е д с т в и е 2: Сумма в-стей противоп. событий равна 1: P(A)+P(A с чертой)=1.
6. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей.Вер-сть события В при усл-и, что А уже произошло, наз. условной в-стью события В. Обозн. РА(В) или Р(В/А). РB(А)= =Р(АВ)/Р(В),Р(В)не равно 0.Отсюда следуют Р(АВ)=РВ(А)Р(В), Р(В)>0 и Р(АВ)= РА(В)Р(А),Р(А)>0.Событие А наз. независимым от события В с вер-стью Р(И) не равной 0, если РВ(А)=Р(А),т. е. вер-сть наступления события А не зависит от того, произошло событие В или нет. Теорема умн-я вер-стей. Вер-сть совместного наступл-я 2 событий равна произвед-ю вер-сти одного из них на усл. в-сть другого, вычисленную в предполож-и, что первое событие уже наступило: Р(АВ)=Р(А)РА(В). В частности для независ. событий Р(АВ)=Р(А)Р(В), т. е. в-сть совместного наступл-я 2 независ. событий равна произв-ю вер-стей этих событий.
7. Теорема сложения вероятностей совместных событий.Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.
Теорема. В-сть появл-я хотя бы 1 из 2 совм. событий равна сумме вер-стей этих событий без вер-сти их совм. появл-я: Р(А + В)=Р(А) + Р(В) – Р(АВ). Док-во: Пусть n – число всех элемент. исходов опыта, k – число исходов, благоприятств. событию А, l – число исходов, благоприятств. событию В, m – число исходов, одновременно благопр. А и В. А+В=k+l-m. P(А+В)=(k+l-m)/n=k/n+l/n+m/n=P(A)+P(B)-P(AB). Т-ма м. б. обобщена на любое конечн. число совм.событий: P(A1+A2+A3+…+An)=P(A1)+P(A2)+P(A3)+…+P(An)-P(A1A2)-P(A1A3)-…-P(An-1An)+P(A1A2A3)+…+P(An-2An-1An)-…+(-1)n-1*P(A1A2…An).
8. Вероятность появления хотя бы одного из нескольких независимых событийПусть независимые события А1, А2…Аn имеют одинак. в-сть, равную p. Тогда Вероятность появления хотя бы одного из событий А1, А2,…,Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий, т.е.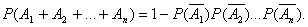 
. В частности, если все n событий имеют одинак. в-сть, равную p, то в-сть появл-я хотя бы 1 из этих событий равна P(А)=1-(1-p)n.
9. Формула полной вероятности. Формулы Байеса.Ф-ла полной вер-ти: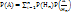 
.Док-во:по условию событие А может произойти с одним из несовместимых событий Н1,Н2,…Нn, тогда использ ф-ла алгебры событий можно записать А=Н1A+Н2A+…+НnА. Cобытия Н1А…НnА несовместимые,т.к. Нi,i=1,n-несоверш, тогда вер-ть событий Р(А)=Р(Н1А)+Р(Н2А)+…+Р(НnА)= Р(Н1)Р(А/Н1)+…+Р(Нn)Р(А/Нn).что и требовалось д-ть.Ф-ла Байеса: 
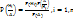,где Р(А) вычисляется по формуле полной вер-ти. Док-во: В силу усл-я А=Н1А+Н2А+ …+НnA. Найдем вер-ть события Р(НiА).По теореме умножения вер-ти имеем Р(НiА)=Р(Нi)P(A/Hi)=P(A)P(Hi/A)
P(Hi/A)=P(Hi)P(A/Hi)/P(A).что и треб д-ть.