Критерии оптимальности в играх с природой

В некоторых играх имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с «природой». Человек в играх с «природой» старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действуют случайно.

Условия игры задаются матрицей .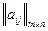

Пусть игрок А имеет стратегии А₁, А₂, ¼, А_m, а природа состояния В₁, В₂, ¼, В_n. Наиболее простой является ситуация, когда известна вероятность р_j каждого состояния природы В_j. При этом, если учтены все возможные состояния, то .

Если игрок А выбирает чистую стратегию А_i, то математическое ожидание выигрыша составит p₁a_i1 + p₂a_i2 + ¼ + p_na_in. Наиболее выгодной будет та стратегия, при которой достигается

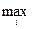(p₁a_i1 + p₂a_i2 + ¼ + p_na_in).

Если информация о состояниях природы мала, то можно применить принцип недостаточного основания Лапласа, согласно которому можно считать, что все состояния природы равновероятны

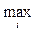(a_i1 + a_i2 + ¼ + a_in)/n,

т.е. стратегию, для которой среднее арифметическое элементов соответствующей строки максимальное.

Имеется ряд критериев, которые используются при выборе оптимальной стратегии.

1. Критерий Вальде. Рекомендуется применять максиминную стратегию. Она достигается из условия

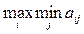
и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека способом.

2. Критерий максимума. Он выбирается из условия

.

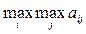Критерий является оптимистический, считается, что природа будет наиболее благоприятна для человека.

3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

,

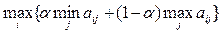где a - степень оптимизма и изменяется в диапазоне [0, 1].

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При a = 1 критерий превращается в критерий Вальде, при a = 0 – в критерий максимума. На a оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем больше последствия ошибочных решений, больше желания застраховаться, тем a ближе к единице.

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии. Элемент матрицы рисков находится по формуле

,

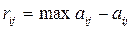где max a_ij – максимальный элемент в столбце исходной матрицы.

Оптимальная стратегия находится из выражения:

.

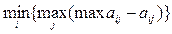При принятии решений в условиях неопределенности следует оценивать различные варианты с точки зрения нескольких критериев. Если рекомендации совпадают, можно с большей уверенностью выбрать наилучшее решение, если рекомендации противоречат друг другу, окончательное решение надо принимать с учетом его сильных и слабых сторон.