Краткие теоретические сведения. Задание. Для линейной стационарной системы управления провести анализ устойчивости, точности в установившемся режиме при отработке типовых воздействий

Калуга, 2013

Задание. Для линейной стационарной системы управления провести анализ устойчивости, точности в установившемся режиме при отработке типовых воздействий, качества переходного процесса.

Цель работы.

1. Научиться проводить анализ линейных непрерывных стационарных систем, определяя:

- устойчивость системы управления по характеру протекающих в ней процессов, по корням характеристического уравнения, по критериям устойчивости;

- точность системы управления в установившемся режиме при отработке типовых воздействия, коэффициенты ошибок;

- прямые и косвенные показатели качества переходного процесса;

Содержание работы:

1. Провести анализ устойчивости заданной замкнутой системы управления:

· по коэффициентам характеристического уравнения системы;

· по нулям и полюсам передаточной функции системы;

· по переходной функции системы;

· по критерию Гурвица;

· по критерию Михайлова;

· по критерию Найквиста.

2. Провести анализ качества переходного процесса системы управления:

· по переходной характеристике замкнутой системы;

· по корням характеристического уравнения замкнутой системы;

· по частотным характеристикам системы.

3. Провести анализ точности системы в установившемся режиме при отработке

типовых воздействий. Определить:

· передаточную функцию замкнутой системы управления по ошибке по задающему воздействию;

· коэффициенты ошибок.

· ошибку системы управления по передаточной функции и теореме о конечном значении функции для заданного воздействия;

4. Провести сравнительный анализ прямых и косвенных показателей качества.

Замечание. При выполнении задания используются данные, полученные в домашних заданиях № 1 и № 2.

Краткие теоретические сведения

В теории управления разработан комплекс требований, определяющих поведение системы при отработке задающего воздействия, который объединяют понятием качества процессов управления.

Задача анализа (исследования) процессов управления - это установить какое влияние оказывает структура системы, значения её параметров на процессы управления.

С точки зрения анализа требования к системе формируются по трём основным направлениям:

· анализ устойчивости системы - нахождение необходимых и достаточных условий затухания переходного процесса. Некоторый запас устойчивости обеспечивает нормальное функционирование системы;

· анализ точности в установившемся режиме - изучение поведения системы в установившемся режиме. Точность в установившемся режиме количественно определяется по величине ошибки при различных воздействиях и зависит от структуры системы и вида входного воздействия;

· анализ качества переходного процесса - изучение поведения системы в переходном режиме. В основе анализа лежат показатели качества, определяемые целью управления.

1. Анализ устойчивости системы

Устойчивость – это способность системы возвращаться в исходный или близкий к нему установившийся режим после выхода из него в результате какого-либо воздействия.

Рассмотрим дифференциальное уравнение движения системы управления, записанное для регулируемой величины 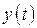и задающего воздействия 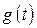, записанное в операторной форме:

.

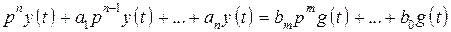Переходный процесс 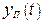определяется полюсами передаточной функции (корнями знаменателя ПФ или видом левой части дифференциального уравнения).

В понятие устойчивости входит только факт наличия или отсутствия затухания переходного процесса (быстрота и форма переходного процесса не имеют значения), поэтому определим свойства корней, при которых система будет устойчивой.

Общее условие устойчивости линейных систем

Общее решение однородного дифференциального уравнения ищется в виде

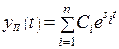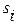, где -корни характеристического полинома А(s)=0.

Для затухания переходного процесса необходимо, чтобы вещественные части корней были отрицательными, т.е. лежали в левой полуплоскости плоскости корней.

Рис.1 Комплексная плоскость

Мнимая ось плоскости корней служит границей устойчивости. Поведение системы на границе устойчивости теорий управления не рассматривается, т.к. т.к. работоспособная система управления должна быть устойчива с запасом и не приближаться к границе устойчивости.

Для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней.

Необходимое условие устойчивости

Рассмотрим характеристический полином системы

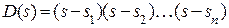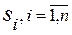, где - корни характеристического уравнения.

Если вещественные части корней характеристического уравнения отрицательные, то оно будет иметь следующий вид:

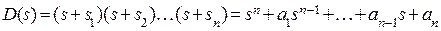
Раскрывая скобки, получим уравнение, где все коэффициенты будут положительными.

Вывод: Необходимым условием устойчивости системы является положительность всех коэффициентов характеристического уравнения, т.е.

.

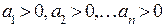Для систем первого и второго порядка необходимое условие устойчивости является и достаточным.

Для систем более высокого порядка этого условия устойчивости недостаточно.

Если хотя бы один из корней характеристического уравнения будет лежать в правой полуплоскости, то в уравнении появятся отрицательные коэффициенты.

Например: 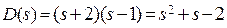или

.

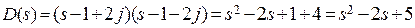Критерии устойчивости

Для определения устойчивости системы без вычисления корней характеристического уравнения были разработаны критерии устойчивости. С помощью критериев устойчивости можно не только определить устойчивость системы, но и выяснить, как влияют на устойчивость системы изменения её параметров, а также структурные изменения в системе.

Критерии устойчивости разделяются на алгебраические и частотные.

С математической точки зрения критерии эквиваленты, однако, выбор определённого критерия позволяет провести анализ устойчивости системы наиболее простым путём.

Критерии, которые позволяют судить об устойчивости системы с помощью алгебраических процедур над коэффициентами характеристического уравнения, называют алгебраическими.

Критерии, которые позволяют судить об устойчивости системы по виду частотных характеристик системы, называют частотными.

Достоинством частотных критериев является их наглядность, а также возмож-ность использовать частотные характеристики, полученные экспериментально, когда не известны дифференциальные уравнения системы или параметры ее элементов.

Критерий устойчивости Гурвица

Для характеристического уравнения 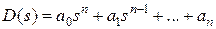составим квадратную матрицу, содержащую 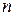строк и 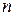столбцов.

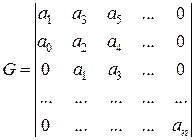
Правило формирования определителя Гурвица: По главной диагонали от левого верхнего до правого нижнего угла вписываются все коэффициенты по порядку от 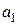до 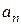. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечётными и чётными индексами.

В случае отсутствия данного коэффициента на его месте записывается «0».

Критерий устойчивости сводится к тому, что при 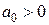должны быть больше нуля все 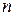определителей Гурвица, получаемых из квадратной матрицы коэффициентов. Выделим в главном определителе Гурвица диагональные миноры и получим определители Гурвица более низкого порядка. Номер определителя определяется номером коэффициента, для которого составляется определитель.

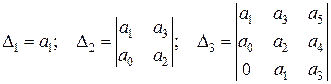и т.д.

Сформулируем критерий Гурвица:

Для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители данной системы были положительными при 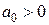, т.е.

.

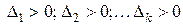В случае, если определитель Гурвица равен 0, то система находится на границе устойчивости, т.е. 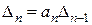. Последнее равенство возможно в двух случаях: 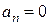или 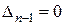. В первом случае система находится на границе апериодической устойчивости (один корень характеристического уравнения нулевой), во втором случае – на границе колебательной устойчивости (характеристическое уравнение имеет пару чисто мнимых корней).

Критерий устойчивости Михайлова

Пусть характеристическое уравнение системы имеет вид:

.

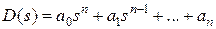Если все корни уравнения находятся в левой части комплексной плоскости 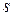, то система устойчива, тогда в правой части плоскости корней нет, т.е. 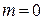и изменение аргумента кривой Михайлова: .

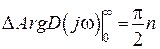Вывод: Система управления является устойчивой, если при возрастании частоты 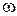от 0 до 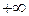изменение (приращение) аргумента вектора 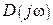будет равно 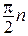, где 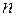— степень характеристического уравнения .

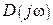При изменении частоты 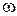от 0 до 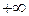вектор 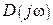на комплексной плоскости опишет своим концом кривую, которая называется характеристической кривой, или годографом вектора .

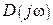Уравнение характеристической кривой определяют подстановкой 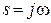в многочлен 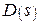и последующим разделением действительной и мнимой частей:

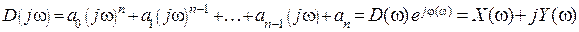, где

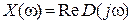- действительная часть годографа Михайлова;

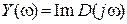- мнимая часть годографа Михайлова;

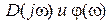- модуль и фаза годографа Михайлова.

Рассмотрим :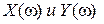

.

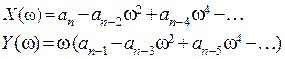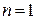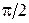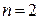На рис. приведены характеристики, соответствующие устойчивой системе. При изменение аргумента равно , при изменение аргумента равно 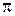и характеристическая кривая проходит через два квадранта, и т.д.

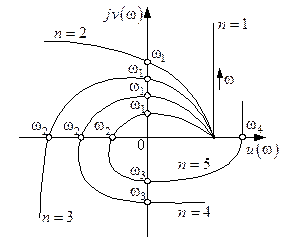
Рис.2 Характеристические кривые (годографы) для устойчивых систем ( )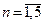

Построение кривой Михайлова можно провести методом контрольных точек, соответствующих фиксированным значениям частоты 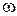, включая частоты пересечения кривой с осями координат, которые находятся как корни уравнени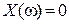й и .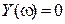

Анализируя годографы Михайлова, можно установить следующее следствие из критерия устойчивости. При последовательном прохождении квадрантов кривая Михайлова пересекает вещественную и мнимую оси поочерёдно ( 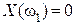, 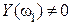; или 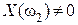, 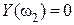и т.д.). Значения частот, при которых происходит пересечение кривой Михайлова с вещественной и мнимой осью, находятся как корни уравнени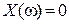й и .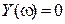

Если принять, что 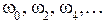- корни 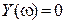, причём 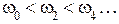, а

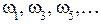- корни 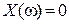, причём 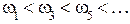., то для устойчивой системы обязательно соблюдение неравенства .

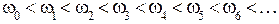Для устойчивости системы корни системы должны перемежаться и быть вещественными, а сумма корней должна быть равна порядку уравнения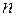

Критерий Михайлова можно записать в другой форме:

Для того чтобы система была устойчива, необходимо и достаточно, чтобы вещественная 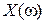и мнимая 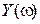функции Михайлова, приравненные к нулю, имели действительные и перемежающиеся корни, причём общее число корней равно порядку 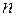характеристического уравнения.

Условие перемежаемости частот позволяет отказаться от построения кривой Михайлова.

Критерий устойчивости Найквиста

Критерий позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики 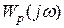разомкнутой системы.

Система устойчива в разомкнутом состоянии.

Если разомкнутая система устойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении частоты 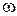от 0 до 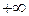годограф разомкнутой системы 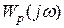не охватывал критическую точку 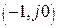в положительном направлении (против часовой стрелки).

Система неустойчива в разомкнутом состоянии.

Если разомкнутая система неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении частоты 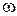от 0 до 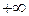годограф разомкнутой системы 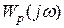охватывал критическую точку 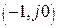в положительном направлении l/2 раз, где l — число правых корней характеристического уравнения разомкнутой системы.

При сложной форме годографа 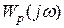могут возникнуть затруднения при определении числа её оборотов вокруг критической точки 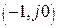. В этом случае используют правило переходов, предложенное Я.З. Цыпкиным.

Назовём переход характеристики 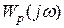) через отрезок вещественной отрицательной полуоси левее критической точки 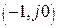положительным, если он происходи сверху вниз, и отрицательным, если он происходит снизу верх. Если характеристика начинается или заканчивается на отрезке левее критической точки 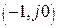, то в этих случаях она совершает полперехода.

Если разомкнутая система неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении частоты 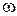от 0 до 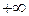сумма отрицательных и положительных переходов годографа разомкнутой системы 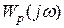через отрезок вещественной отрицательной полуоси левее критической точки 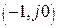была равна l/2 раз, где l — число правых корней характеристического уравнения разомкнутой системы.

АФЧХ разомкнутых статических систем при изменении частоты 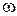от 0 до 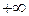образуют замкнутый контур.

У астатических разомкнутых систем при 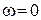годограф 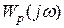начинается в бесконечности. Для определения устойчивости систем с астатизмом любого порядка необходимо начало АФЧХ разомкнутой системы 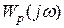мысленно дополнить дугой бесконечного радиуса против часовой стрелки до пересечения с вещественной положительной полуосью (т.е. сделать контур замкнутым) и применить соответствующее правило по критерию устойчивости Найквиста.

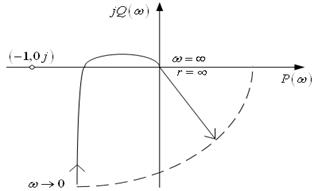
Рис.3 Критерий Найквиста для астатических систем