Построение области устойчивости в плоскости варьируемых параметров

1. Передаточная функция разомкнутой системы равна:

W(p)=Wрег(Р)*Wим(Р)*Wр.о(Р)*Wоб(Р)*Wд(Р)=

=(К₁Р+К₂)*Ким*Кро*К₀ е^-рτ *Кд / Р(1+ТР)

Обозначим К=(К₁Р+К₂)*Ким*Кро*К₀ е^-рτ *Кд / Р(1+ТР) =

=-5,5*124*0,0104*0,06=-0,425

Тогда :

W(p)= К е^-рτ(К₁Р+К₂) / Р(1+ТР)

2. Передаточная функция замкнутой системы по каналу управления :

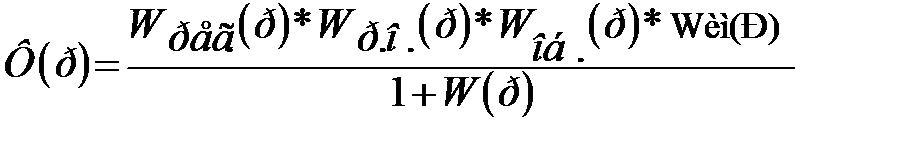
3.Передаточная функция замкнутой системы по возмущению :

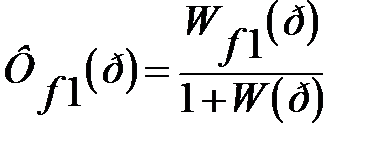
Характеристический полином замкнутой системы получим из выражения:

1+W(p)=1+Ке^-рτ(К₁+К₂) / Р(1+Тр)=0

отсюда Д(р)=Тр²+р(1+К₁Ке^-рτ)+КК₂е^-рτ=0

1.Уравнение апериодической границы устойчивости соответствует р=0.

Получаем: КК₂=0 или К₂=0

2.Граница ,соответствующая бесконечному корню отсутствует, так как Т не может быть равно нулю по условию.

3.Найдем колебательную границу устойчивости.Для этого подставим р=Јω.

Д(Јω)=-Тω²+ Јω(1+КК₁(cosωτ-Јsinωτ))+КК₂(cosωτ-Јsinωτ)

тогда:

U(ω)= -Тω²+ω КК₁sinωτ+КК₂ cosωτ=0

V(ω)= ω+ω КК₁cosωτ-КК₂ sinωτ=0

Решив уравнение относительно К₁ и К₂ , найдем выражение для колебательной границы устойчивости в виде:

К₁= Тω sinωτ- cosωτ / К

К₂= ω(sinωτ+ Тω cosωτ) / К

Рассчитаем 3 точки колебательной границы устойчивости при ω=0, ∆ω, 2∆ω.Результаты занесем в таблицу 3.

Таблица3.

w [c-1]		0,005	0,01
К1	2,3498	1,0415	-2,3105
К2		-0,0150	-0,0427

РЕЗУЛЬТАТЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

ОДНОКОНТУРНОЙ ТИПОВОЙ НЕПРЕРЫВНОЙ АВТОМАТИЧЕСКОЙ СИСТЕМЫ

14.10.10

********************************************************************

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :

(апериодическое звено 1-го порядка с запаздыванием)

K * Exp(-Tau*P)

W(P) = ----------------- .

1 + T*P

ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :

Коэффициент передачи K = -5.500

Постоянная времени T = 180.000

Запаздывание Tau = 100.000

********************************************************************

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ РЕГУЛЯТОРА С ПИ - ЗАКОНОМ УПРАВЛЕНИЯ:

K1*P + K2

W(P) = --------------- .

P

НАСТРОЙКИ РЕГУЛЯТОРА :

K1 - ПРОПОРЦИОНАЛЬНАЯ СОСТАВЛЯЮЩАЯ ;

К2 - ИНТЕГРАЛЬНАЯ СОСТАВЛЯЮЩАЯ .

********************************************************************

ЭЛЕМЕНТОВ СИСТЕМЫ УПРАВЛЕНИЯ - УСИЛИТЕЛЬНЫЕ ЗВЕНЬЯ .

ПАРАМЕТРЫ ЭЛЕМЕНТОВ:

Коэффициент передачи ДАТЧИКА 0.060

Коэффициент передачи ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА 124.000

Коэффициент передачи РЕГУЛИРУЮЩЕГО ОРГАНА 0.010

********************************************************************

РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ

НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СИСТЕМЫ

В ПЛОСКОСТИ ПАРАМЕТРОВ К1 и К2 ПИ-РЕГУЛЯТОР

УРАВНЕНИЯ ГРАНИЦ ОБЛАСТИ:

АПЕРИОДИЧЕСКАЯ ГРАНИЦА - К2 < 0 ,

КОЛЕБАТЕЛЬНАЯ ГРАНИЦА УСТОЙЧИВОСТИ ЗАДАЕТСЯ В ВИДЕ ТАБЛИЦЫ

W K1 K2

0,0000 2,3498 0,0000

0,0013 2,2651 -0,0010

0,0025 2,0133 -0,0040

0,0038 1,6016 -0,0088

0,0050 1,0415 -0,0150

0,0063 0,3488 -0,0221

0,0075 -0,4567 -0,0295

0,0088 -1,3519 -0,0367

0,0100 -2,3105 -0,0427

0,0113 -3,3042 -0,0470

0,0125 -4,3029 -0,0487

0,0138 -5,2754 -0,0472

0,0150 -6,1905 -0,0416

0,0163 -7,0173 -0,0316

0,0175 -7,7262 -0,0167

0,0188 -8,2897 0,0034

0,0201 -8,6829 0,0289

Область устойчивости системы в плоскости варьируемых параметров

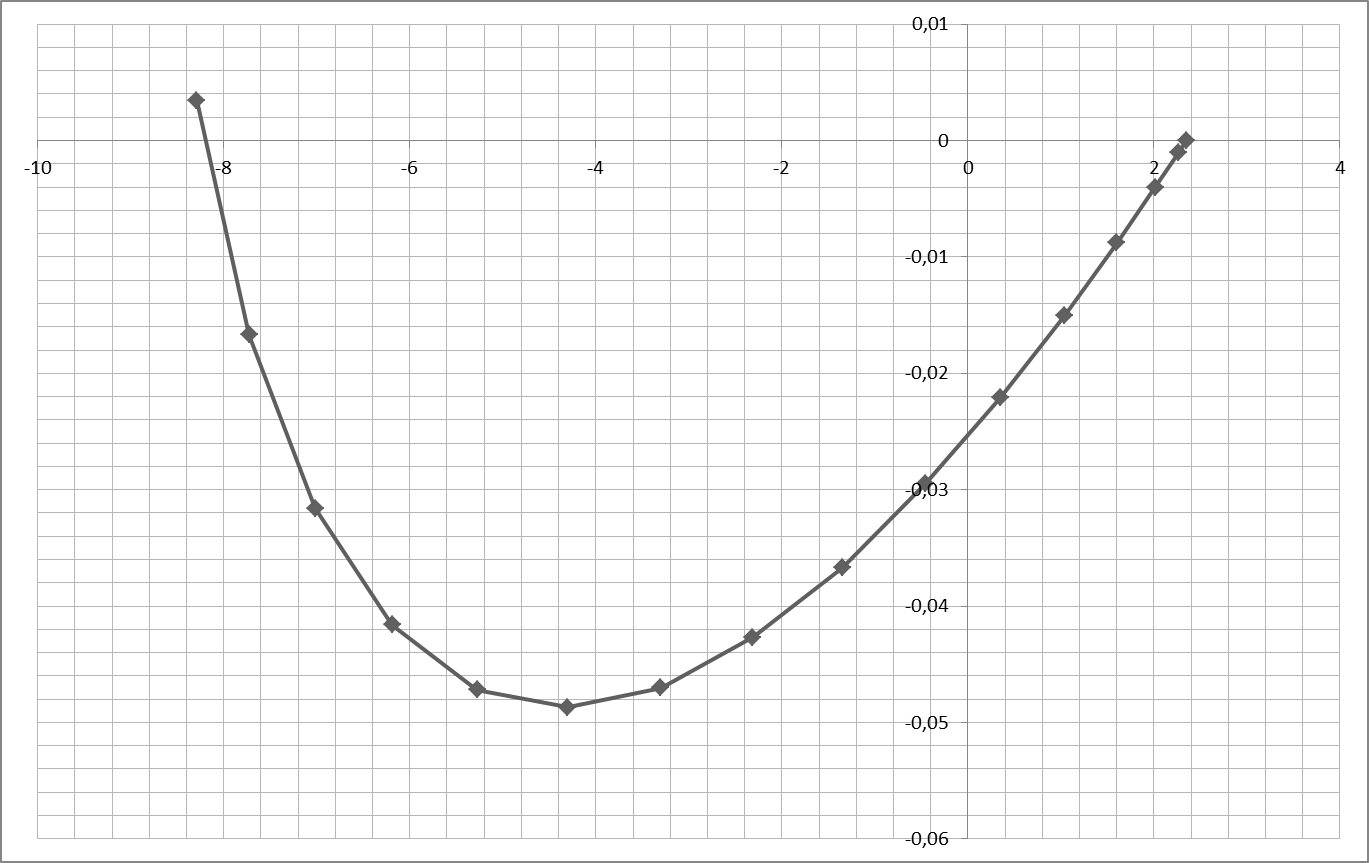
Определение направления вида.штриховки колебательной границы устойчивости производится в соответствии со знаком определителя вида

D(w)= == =

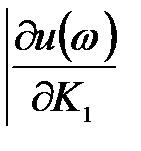
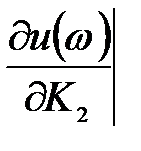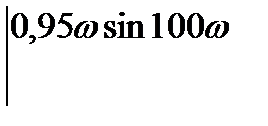
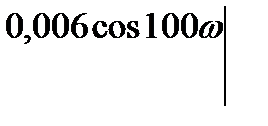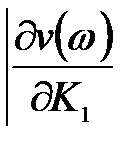
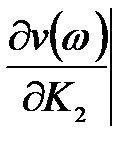
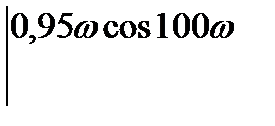
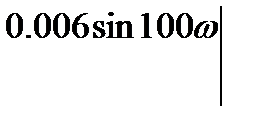
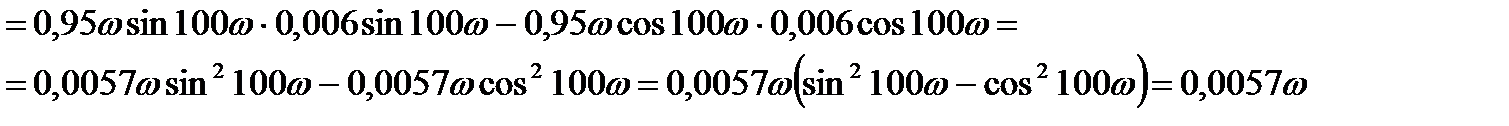
При перемещении вдоль колебательной границы в направлении возрастании частоты от 0 до ¥ кривая штрихуется слева, т. к. Dw > 0. Если частоту менять в пределах от - ¥ до 0 (w < 0), то определитель меняет знак и, двигаясь вдоль увеличения частоты, нужно штриховать правую часть кривой. Таким образом, кривая колебательной границы проходится дважды, при этом штрихуется одна и та же часть кривой двойной штриховкой. Апериодическая граница устойчивости штрихуется в сторону колебательной границы устойчивости.

Параметры регулятора K₁ ,K₂, выбранные из области устойчивости системы, обеспечат затухание переходной составляющей её движения при любых начальных отклонениях и внешних воздействиях.Однако это недостаточно для оценки системы с точки зрения её практической пригодности