Построение области устойчивости

Рассмотрим, как строится область устойчивости многошагового метода. Преобразуем полиномиальное уравнение 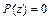следующим образом:

,

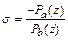где

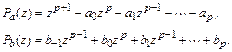
Будем считать, что 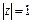и вычислим соответствующее 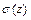. Так как любое 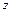на единичной окружности 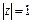в комплексной плоскости 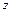можно выразить в виде

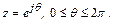
то

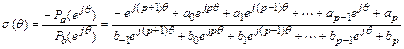
представляет множество точек границы области устойчивости на комплексной плоскости 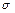(геометрическая иллюстрация такого преобразования приведена на рис. 13.1). Нетрудно проверить, что кривая 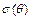симметрична относительно оси 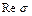. Поэтому преобразование выполняют только для углов 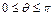. Границу области устойчивости метода для углов 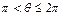восстанавливают путем симметричного

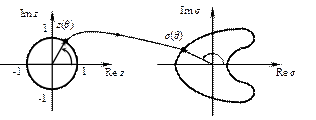
Рис. 13.1. Геометрическая иллюстрация построения области

устойчивости в плоскости σ

отображения кривой 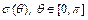относительно оси .

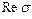Покажем теперь области устойчивости многошаговых методов различных порядков точности (от первого до шестого), построенные в плоскости 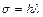по описанной методике (см. рис. 13.2, 13.3, 13.4).

Из рисунков следует, что размер области устойчивости линейных многошаговых методов (как явных, так и неявных) уменьшается с увеличением порядка точности. Наибольшая область устойчивости характерна для методов первого порядка точности, наименьшая – для методов шестого порядка точности.

Условие устойчивости явных многошаговых методов Адамса, впрочем, как и неявных методов Адамса выше второго порядка точности, накладывает существенные ограничения на величину шага интегрирования. По этой причине эти методы не подходят для решения жестких задач. Жесткие дифференциальные уравнения целесообразно ин-тегрировать неявными методами Адамса первого либо второго порядков точности, а также неявными методами Гира.

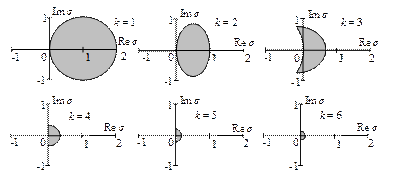
Рис. 13.2. Области устойчивости явных многошаговых методов Адамса

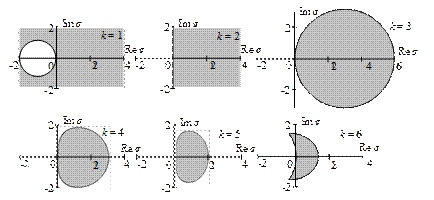
Рис. 13.3. Области устойчивости неявных многошаговых методов Адамса

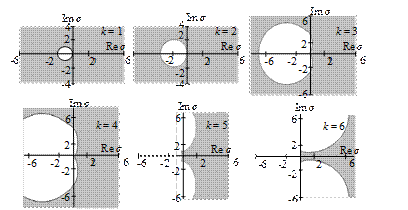
Рис. 13.4. Области устойчивости неявных многошаговых методов Гира

Определение 1. Метод называется 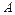-устойчивым, если его область устойчивости содержит всю правую полуплоскость комплексной плоскости .

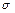Свойство 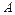-устойчивости метода позволяет выбирать шаг интегрирования исходя только из требования точности. 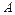-устойчивыми являются неявные методы Адамса и Гира первого и второго порядков точности.

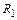Определение 2. Метод называется жестко устойчивым, если его область устойчивости содержит две подобласти и 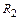(см. рис. 13.5) комплексной плоскости 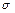, где 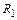определяется условиями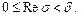 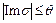, 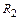– условием 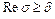, причем в области 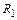метод обеспечивает требуемую точность.

Сущность требования 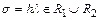заключается в том, чтобы при малых 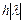, когда 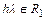, обеспечить требуемую точность быстрых составляющих решения, а при больших 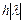гарантировать затухание быстрых составляющих, не учитывая погрешность их воспроизведения.

Жестко устойчивые методы численного интегрирования позволяют эффективно решать жесткие системы обыкновенных дифференциальных уравнений, так как шаг интегрирования в этих методах ограничивается только условием допустимой погрешности.

Анализ областей устойчивости методов Гира от третьего до шестого порядков включительно свидетельствует о том, что эти методы относятся к классу жестко устойчивых (методы Гира более высоких порядков не являются жестко устойчивыми). В частности, для метода третьего порядка 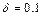, для четвертого порядка 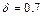, для пятого порядка 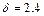, для метода шестого порядка .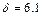