Часть 4. Целевая функция
Создадим математическую модель процесса с коэффициентами a1=8 и T=1 и подберем их таким образом, чтобы при данных значениях целевая функция была минимальна.
Выберем шаг h = 0.2. Точность EPSILON = 0.0001. Количество итераций ITERATION_AMOUNT = 1000.
Результаты пошагового приближения показаны в таблице 3 “Зависимость CF от значений a1 и T”, график CF представлен на рис.7
CF1min = 8,901453
CF2min = 44,05068
CF3min = 132,7882
Таблица 3
«Зависимость CF от значений параметров a1 и T»
| № шага | A1 | T | CF1 (m=0,005) | CF2 (m=0,01) | CF 3(m=0,02) |
| 1,884E+12 | 1,884E+12 | 1,884E+12 | |||
| 1,884E+12 | 1,884E+12 | 1,884E+12 | |||
| 7,8 | 1,784E+12 | 1,784E+12 | 1,784E+12 | ||
| 7,6 | 1,686E+12 | 1,686E+12 | 1,686E+12 | ||
| 7,4 | 1,591E+12 | 1,591E+12 | 1,591E+12 | ||
| 7,2 | 1,499E+12 | 1,499E+12 | 1,499E+12 | ||
| 1,409E+12 | 1,409E+12 | 1,409E+12 | |||
| 6,8 | 1,323E+12 | 1,323E+12 | 1,323E+12 | ||
| 6,6 | 1,239E+12 | 1,239E+12 | 1,239E+12 | ||
| 6,4 | 1,158E+12 | 1,158E+12 | 1,158E+12 | ||
| 6,2 | 1,079E+12 | 1,079E+12 | 1,079E+12 | ||
| 1,004E+12 | 1,004E+12 | 1,004E+12 | |||
| 5,8 | 9,309E+11 | 9,309E+11 | 9,309E+11 | ||
| 5,6 | 8,609E+11 | 8,609E+11 | 8,609E+11 | ||
| 5,4 | 7,936E+11 | 7,936E+11 | 7,936E+11 | ||
| 5,2 | 7,291E+11 | 7,291E+11 | 7,291E+11 | ||
| 6,673E+11 | 6,673E+11 | 6,673E+11 | |||
| 4,8 | 6,083E+11 | 6,083E+11 | 6,083E+11 | ||
| 4,6 | 5,521E+11 | 5,521E+11 | 5,521E+11 | ||
| 4,4 | 4,987E+11 | 4,987E+11 | 4,987E+11 | ||
| 4,2 | 4,48E+11 | 4,48E+11 | 4,48E+11 | ||
| 4,001E+11 | 4,001E+11 | 4,001E+11 | |||
| 3,8 | 3,55E+11 | 3,55E+11 | 3,55E+11 | ||
| 3,6 | 3,126E+11 | 3,126E+11 | 3,126E+11 | ||
| 3,4 | 2,73E+11 | 2,73E+11 | 2,73E+11 | ||
| 3,2 | 2,362E+11 | 2,362E+11 | 2,362E+11 | ||
| 2,021E+11 | 2,021E+11 | 2,021E+11 | |||
| 2,8 | 1,708E+11 | 1,708E+11 | 1,708E+11 | ||
| 2,6 | 1,423E+11 | 1,423E+11 | 1,423E+11 | ||
| 2,4 | 1,166E+11 | 1,166E+11 | 1,166E+11 | ||
| 2,2 | 9,359E+10 | 9,359E+10 | 9,359E+10 | ||
| 7,337E+10 | 7,337E+10 | 7,337E+10 | |||
| 1,8 | 5,592E+10 | 5,592E+10 | 5,592E+10 | ||
| 1,6 | 4,124E+10 | 4,124E+10 | 4,124E+10 | ||
| 1,4 | 2,933E+10 | 2,933E+10 | 2,933E+10 | ||
| 1,2 | 2,019E+10 | 2,019E+10 | 2,019E+10 | ||
| 1,381E+10 | 1,381E+10 | 1,381E+10 | |||
| 0,8 | 1,021E+10 | 1,021E+10 | 1,021E+10 | ||
| 0,6 | 9,37E+09 | 9,37E+09 | 9,371E+09 | ||
| 0,6 | 1,2 | 586850,911 | 585505,007 | 588790,108 | |
| 0,6 | 1,4 | 124642,353 | 124498,296 | 125774,153 | |
| 0,6 | 1,6 | 105470,917 | 105284,132 | 105939,099 | |
| 0,6 | 1,8 | 98001,114 | 98219,831 | 98781,217 | |
| 0,8 | 1,8 | 94310,316 | 94510,650 | 95055,002 | |
| 1,8 | 90793,658 | 90975,608 | 91502,927 | ||
| 1,2 | 1,8 | 87451,139 | 87614,705 | 88124,991 | |
| 1,4 | 1,8 | 84282,760 | 84427,942 | 84921,195 | |
| 1,6 | 1,8 | 81288,521 | 81415,318 | 81891,538 | |
| 1,8 | 1,8 | 78468,421 | 78576,834 | 79036,021 | |
| 1,8 | 75822,460 | 75912,490 | 76354,643 | ||
| 2,2 | 1,8 | 73350,640 | 73422,285 | 73847,405 | |
| 2,4 | 1,8 | 71052,958 | 71106,220 | 71514,306 | |
| 2,6 | 1,8 | 68929,416 | 68964,294 | 69355,347 | |
| 2,8 | 1,8 | 66980,014 | 66996,507 | 67370,527 | |
| 1,8 | 65204,751 | 65202,860 | 65559,847 | ||
| 3,2 | 1,8 | 63603,628 | 63583,353 | 63923,306 | |
| 3,4 | 1,8 | 62176,644 | 62137,985 | 62460,905 | |
| 3,6 | 1,8 | 60923,800 | 60866,757 | 61172,644 | |
| 3,8 | 1,8 | 59845,095 | 59769,668 | 60058,522 | |
| 1,8 | 58940,529 | 58846,719 | 59118,539 | ||
| 4,2 | 1,8 | 58210,104 | 58097,909 | 58352,696 | |
| 4,4 | 1,8 | 57653,818 | 57523,239 | 57760,992 | |
| 4,6 | 1,8 | 57271,671 | 57122,708 | 57343,429 | |
| 4,8 | 1,8 | 57063,664 | 56896,317 | 57100,004 | |
| 1,8 | 57029,796 | 56844,065 | 57030,719 | ||
| 32987,463 | 33084,055 | 33539,979 | |||
| 5,2 | 30410,132 | 30504,267 | 30945,503 | ||
| 5,4 | 27937,650 | 28029,328 | 28455,877 | ||
| 5,6 | 25570,018 | 25659,237 | 26071,099 | ||
| 5,8 | 23307,234 | 23393,996 | 23791,170 | ||
| 21149,300 | 21233,604 | 21616,090 | |||
| 6,2 | 19096,214 | 19178,060 | 19545,860 | ||
| 6,4 | 17147,978 | 17227,366 | 17580,478 | ||
| 6,6 | 15304,590 | 15381,521 | 15719,945 | ||
| 6,8 | 13566,052 | 13640,525 | 13964,261 | ||
| 11932,362 | 12004,378 | 12313,427 | |||
| 7,2 | 10403,522 | 10473,079 | 10767,441 | ||
| 7,4 | 8979,530 | 9046,630 | 9326,304 | ||
| 7,6 | 7660,388 | 7725,030 | 7990,017 | ||
| 7,8 | 6446,094 | 6508,279 | 6758,578 | ||
| 5336,650 | 5396,377 | 5631,989 | |||
| 8,2 | 4332,055 | 4389,323 | 4610,248 | ||
| 8,4 | 3432,308 | 3487,119 | 3693,356 | ||
| 8,6 | 2637,411 | 2689,764 | 2881,314 | ||
| 8,8 | 1947,362 | 1997,258 | 2174,120 | ||
| 1362,163 | 1409,601 | 1571,776 | |||
| 9,2 | 881,813 | 926,793 | 1074,280 | ||
| 9,4 | 506,311 | 548,834 | 681,634 | ||
| 9,6 | 235,659 | 275,724 | 393,836 | ||
| 9,8 | 69,856 | 107,463 | 210,888 | ||
| 8,901 | 44,051 | 132,788 |
N = 91
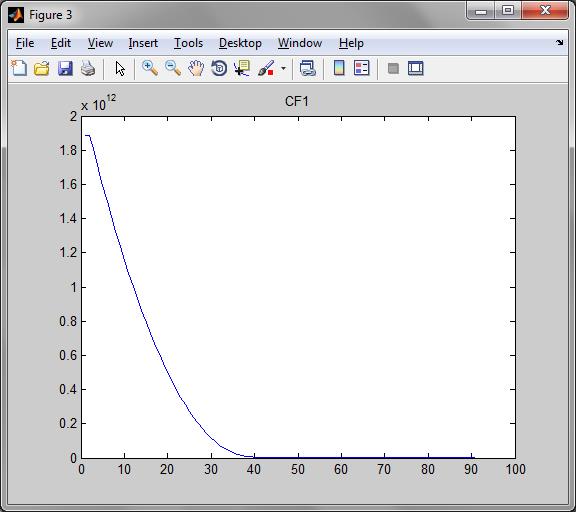
(рис.7)
Листинг программы:
1. %Часть 2. Оптимизация покоординатно.
2. function SecondPart_OptimizationCoordinate(function_name, h, EPSILON, ITERATION_AMOUNT, a, b)
3.
4. global x;
5. global y;
6.
7. %Перем. для пропуска проверки условия на то, предыд. y min из последних трех или нет.
8. change_coord = 1;
9. %Для выхода из цикла, если кол-во. итераций больше ITERATION_AMOUNT.
10. number_iteration = 1;
11.
12. change = 1;
13. constant = 2;
14. i = 2;
15.
16. x(1,1) = 2; %первая координата, первое значение.
17. x(2,1) = 2; %вторая координата, первое значение.
18. x(1,2) = x(change,i-1) + h; %первая координата, второе значение.
19. x(2,2) = x(constant,i-1); %вторая координата, второе значение.
20.
21. y(1) = EllipseFunct_or_FunctRosenbrock(function_name, x(1,1), x(2,1), a, b);
22. new_value_of_function = EllipseFunct_or_FunctRosenbrock(function_name, x(1,2), x(2,2), a, b);
23.
24. if new_value_of_function > y(1)
25. h = h* (-1);
26. x(1,2) = x(change,i-1) + h;
27. y(2) = EllipseFunct_or_FunctRosenbrock(function_name, x(change,i), x(constant,i), a ,b);
28.
29. else
30. y(2) = new_value_of_function;
31. end
32.
33. %Цикл пока модуль разности функций больше точности эпсилон и количество итераций меньше ITERATION_AMOUNT(10000).
34. while (abs(y(i)-y(i-1)) > EPSILON && (number_iteration < ITERATION_AMOUNT))
35.
36. number_iteration = number_iteration + 1;
37. i = i + 1;
38. change_coord = change_coord + 1;
39.
40. %прибавляем шаг к первой координате.
41. x(change,i) = x(change,i-1) + h;
42. %вторую координату переписываем.
43. x(constant,i) = x(constant,i-1);
44. %находим значение функции от новых значений.
45. new_value_of_function = EllipseFunct_or_FunctRosenbrock(function_name, x(1,i), x(2,i), a, b);
46.
47. %если функция от текущих значений больше функции от предыдущих, то h = h* (-1), ... иначе y(i) = new_value_of_function.
48. if new_value_of_function > y(i-1)
49.
50. %обнуляем последнее значение
51. x(change,i) = NaN;
52. i = i - 1; %чтобы вернуться к предыдущему минимальному значению функции
53. h = h* (-1);
54.
55. %Если после смены координаты, по которой шагаем сделали не меньше 3 точек, то делаем проверку min y из последних 3-х. значений.
56. if (change_coord >= 3)
57.
58. %если функция от значений на предыдущем шаге меньше текущих и меньше чем на шаге i-2, то меняем координату перемещения.
59. if y(i-1) >= y(i)
60.
61. %После перемены координаты по которой шагаем - обнуляем change_coord.
62. change_coord = 0;
63. if (constant == 1)
64. constant = 2;
65. change = 1;
66.
67. else
68. constant = 1;
69. change = 2;
70. end
71.
72. end
73. end
74.
75. else
76. y(i) = new_value_of_function;
77. end
78. end %конец цикла while
79.
80. %=====================Графическая часть==========================
81. %построение графика
82. x_contour = -5:0.1:5;
83. y_contour = -5:0.1:5;
84. [X, Y] = meshgrid(x_contour, y_contour);
85.
86. if strcmp(function_name, 'ELLIPSE') == 1
87. title_plot = ('Функция Эллипса');
88. Z = (X/a).^2 + (Y/b).^2;
89. min_x = 0;
90. min_y = 0;
91. contour_amount = 50;
92.
93. elseif strcmp(function_name, 'ROSENBROCK') == 1
94. title_plot = ('Функция Розенброка');
95. Z = 100 * (Y - X.^2).^2 + (1 - X).^2;
96. min_x = 1;
97. min_y = 1;
98. contour_amount = 200;
99. end
100.
101. %figure
102. %mesh(X,Y,Z);
103. figure
104. contour(X, Y, Z, contour_amount);
105. % отображение меток уровня
106. hold on;
107. plot(x(1, :), x(2, :), '<-');
108. %вывод точки минимума.
109. plot(min_x, min_y, 'r*');
110. title(title_plot);
111. text(min_x-0.2, min_y-0.4,'MIN')
112. % выводначальной точки на график
113. text(x(1,1), x(2,1), 'A0', ...
114. 'BackgroundColor',[.7 .7 .7]);
115. % вывод решения на график
116. text(-4.9, -3.9, ...
117. char(['x1 = ' num2str(x(1,i))], ...
118. ['x2 = ' num2str(x(2,i))], ...
119. ['y = ' num2str(y(i))], ...
120. ['итераций - ' num2str(number_iteration)]), ...
121. 'BackgroundColor',[.7 .7 .7]);
122. end
Код функции y = EllipseFunct_or_FunctRosenbrock:
1. %Функция для вычисления значения ф-ии. F(x1, x2) по Розенброку или по ф-ии. Эллипса.
2. function y = EllipseFunct_or_FunctRosenbrock(function_name, x_0_i, x_1_i, a, b)
3.
4. if strcmp(function_name, 'ROSENBROCK') == 1
5. y = 100 * (x_1_i - x_0_i.^2).^2 + (1 - x_0_i).^2;
6. return
7.
8. elseif strcmp(function_name, 'ELLIPSE') == 1
9. y = x_0_i.^2/a.^2 + x_1_i.^2/b.^2;
10. return
11. else
12. y = -1;
13. return
14. end
15. end
