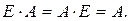Некоторые сведения из теории матриц

Матрицы необходимы при использовании модели динамики системы в виде переменных состояния, для исследования многомерных систем. Матрица представляет таблицу из m строк и n столбцов:

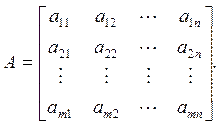
Говорят, что в этом случае размерность (англ. dimention) матрицы равна (m×n). Это можно записать следующим образом:

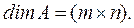
Основные типы матриц

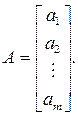
1. Матрица-столбец(m×1):

2. Матрица-строка(1×n):

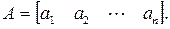
3. Диагональная матрица. Главная диагональ квадратной матрицы состоит из элементов a_ii. Диагональной матрицей называется квадратная матрица, элементы которой, не лежащие на главной диагонали, равны нулю:

.

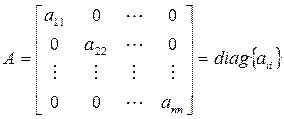4. Единичная матрица. Единичной матрицей называется диагональная матрица, диагональные элементы которой равны единице:

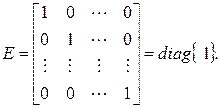
5. Нулевая матрица. Матрица, все элементы которой тождественно

равны нулю, называется нулевой матрицей:

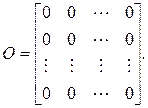
6. Транспонированная матрица. Это матрица A^T размерности (n×m),в

которой строки и столбцы меняются местами по отношению к исходной матрице А размерности (m×n), т.е. если A = [a_ij], то A^T = [a_ji]:

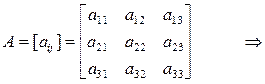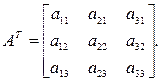Специальные типы матриц

1. Симметрическая матрица. Квадратная матрица (m = n) с действительными элементами называется симметрической, если она равна своей транспонированной, т.е. если

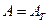, или a_ij = a_ji (i,j=1,2,…, n).

2. Кососимметрическая матрица. Действительная квадратная матрица называется кососимметрической, если

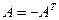,или a_ij = – a_ji (i,j=1,2,…, n).

Элементы, находящиеся на главной диагонали кососимметрической матрицы, равны нулю, т.е. a_ij =0(i=1,…, n).

3. Комплексно-сопряженная матрица. Если элементы матрицы A комплексные (т.е. a_ik = α_ji+jβ_ik, где 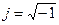), то комплексно сопряженная матрица B содержит элементы b_ik = α_ji – jβ_ik. Это записывается в форме:

B=A*.

4. Сопряженная матрица.Матрица В, сопряженная по отношению к А является транспонированной и комплексно сопряженной по отношению к А, т.е. равна:

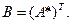
5. Действительная матрица.Матрица А называется действительной, если она равна своей комплексно сопряженной матрице:

A = A*.

6. Мнимая матрица.Матрица А называется мнимой, если она равна своей комплексно сопряженной матрице, взятой со знаком минус:

A = – (A*).

7. Эрмитова матрица.Матрица А называется эрмитовой, если она равна своей сопряженной матрице:

A = (A*)^T.

8. Косоэрмитова матрица.Матрица А называется косоэрмитовой, если она равна своей сопряженной матрице, взятой со знаком минус:

A = – (A*)^T.

Операции над матрицами

Сложение матриц

Складывать можно только матрицы одинаковой размерности. При сложении матриц одноименные элементы слагаемых матриц складываются.

Пример 1. Вычислить сумму указанных матриц.

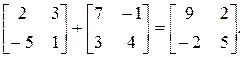
Свойства сложения матриц. Сложение матриц коммутативно и ассоциативно.

1. Коммутативность:

A+B=B+A

2. Ассоциативность:

A+(B+C)=(A+B)+C.

Вычитание матриц осуществляется аналогично сложению, но с учетом знака «минус».

Пример 2. Вычислить разность указанных матриц.

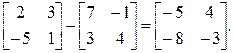
Умножение матриц

Число столбцов матрицы A должно быть равно числу строк матрицы B, тогда говорят, что эти две матрицы согласуются по форме, и произведение AB существует. Если матрица A имеет размерность (m×n), а матрица B имеет размерность (n×k), то матрица C, являющаяся результатом произведения AB=C, будет иметь размерность (m×k). Условно это обозначим так:

.

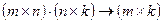Для матриц A (m×n) и B (n×m) существует как произведение AB, так и произведение BA. Произведение AB имеет размерность (m×m), а произведение BA - размерность (n×n). Естественно, что они в общем случае не равны. Даже в случае m=n, а значит, при одинаковой размерности (m×m) произведений AB и BA, эти произведения не обязательно равны. Если же оказывается, что они равны, т.е. AB=BA, то в этом случае говорят, что матрицы коммутативны.

Пример 3. Вычислить произведения указанных матриц:

;

.

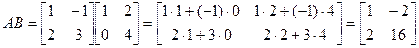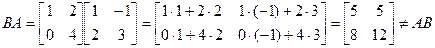Свойства умножения матриц. Умножение в общем случае не коммутативно, ассоциативно и дистрибутивно.

1. Некоммутативность:

AB≠BA.

2. Ассоциативность:

(AB)C=A(BC).

3. Дистрибутивность:

(A+B)C=AC+BC.

Умножение на скаляр.

При умножении на скалярную величину каждый элемент матрицы умножается на него.

Умножение на диагональную матрицу.

Умножение слева матрицы A на диагональную матрицу D эквивалентно операции эквивалентную операции со строками A. При умножении справа матрицы A на диагональную матрицу D операции производятся со столбцами матрицы A.

Умножение транспонированных матриц(транспонирование произведения матриц):

(A∙B)^T = B^T∙A^T.

Умножение на единичную матрицу.

Умножение как слева, так и справа на единичную матрицу не изменяет исходную матрицу, т.е.