Частотные коэффициенты передачи основных звеньев приборов.
Пусть на оптико-электронный прибор (ОЭП) действуют входной сигнал 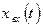 , имеющий спектр
, имеющий спектр 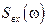 , и совокупность помех и шумов (внешние помехи, шумы фотоприемника, нагрузочной цепи и усилителя электронного тракта), а приемник излучения обладает интегральной вольтовой чувствительностью
, и совокупность помех и шумов (внешние помехи, шумы фотоприемника, нагрузочной цепи и усилителя электронного тракта), а приемник излучения обладает интегральной вольтовой чувствительностью 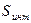 .В этом случае структурную схему такого ОЭП можно представить, как показано на рисунке 2.1.
.В этом случае структурную схему такого ОЭП можно представить, как показано на рисунке 2.1.
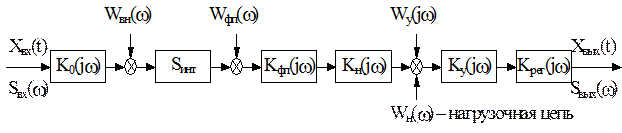
Ко(jw) – оптической системы; Кфп(jw) – фотоприемника;
Кн(jw) – нагрузочной цепи; Ку(jw) – усилителя;
Крег(jw) – регистрирующего прибора.
Рисунок 2.1 – Структурная схема преобразования сигналов
Для информационных и измерительных приборов связь между спектрами входного и выходного сигналов определяется выражениями:
det – 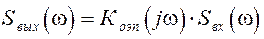 , (2.1)
, (2.1)
случ. – 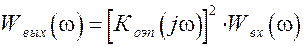 , (2.2)
, (2.2)
где
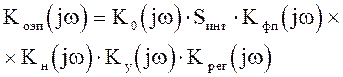 . (2.3)
. (2.3)
Спектральные плотности шумов на выходе схемы зависят от места их приложения и определяются частотным коэффициентом передачи участка цепи между точкой приложения и выходом. Например,
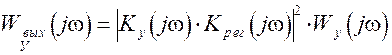 . (2.4)
. (2.4)
Если шумы независимы между собой, то на выходе их спектр
мощности суммируется, т.е.
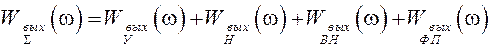 . (2.5)
. (2.5)
Расчет частотных коэффициентов каждого узла системы обработки сигналов производится по формулам, которые учитывают принцип работы оптической системы, тип фотоприемника и его инерционные свойства, тип нагрузочной цепи, а также вид электронного тракта обработки и усиления сигналов.
Расчет общего частотного коэффициента передачи производится путем перемножения полученных функций. При этом необходимо, дискретно изменяя значение частоты, построить график полученной функции.
2.1.1 Оптическая система
С достаточной степенью точности полагают, что
 , (2.6)
, (2.6)
где К0 называют коэффициентом передачи.
Наиболее распространенные варианты работы ОЭП – это работа на основе изменения освещенности входного зрачка (точечный источник) и изменения яркости свечения объекта (протяженный источник). В первом случае можно записать, что световой поток Ф на выходе системы
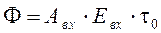 , (2.7)
, (2.7)
где Авх – площадь входного зрачка;
Евх – освещенность на входном зрачке;
t0 – коэффициент пропускания.
Тогда 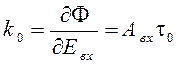 [см2]. (2.8)
[см2]. (2.8)
Во втором случае (источник протяженный) –
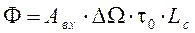 , (2.9)
, (2.9)
где 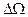 – угловое поле зрения;
– угловое поле зрения;
Lc – яркость источника излучения.
Тогда 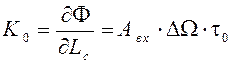 [см2.ср]. (2.10)
[см2.ср]. (2.10)
Возможен и третий случай, когда ОЭП работает на основе изменения площади засветки. Тогда
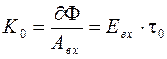
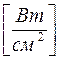 . (2.11)
. (2.11)
2.1.2 Фотоприемники
В области малых и средних частот (f<108 Гц) все фотоприемники считают с динамической точки зрения апериодическими звеньями первого порядка. В этом случае
 , (2.12)
, (2.12)
где Тфп – постоянная времени фотоприемника;
Sинт – интегральная чувствительность по току, если приемник представляется в схеме генератором тока, и интегральная чувствительность по напряжению, если представляется источником ЭДС.
Если область частот принимаемого сигнала больше f>108 Гц и используются ФЭУ, то необходим учет времени прохождения электронов от фотокатода к аноду, а именно:
 , (2.13)
, (2.13)
где 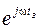 – звено, учитывающее задержку сигнала.
– звено, учитывающее задержку сигнала.
2.1.3 Нагрузочные цепи фотоприемников
Частотные передаточные функции 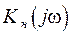 нагрузочных цепей, соединяющих выход фотоприемника с первым каскадом усиления электронного тракта, зависят от типа связи между ними (емкостная или трансформаторная).
нагрузочных цепей, соединяющих выход фотоприемника с первым каскадом усиления электронного тракта, зависят от типа связи между ними (емкостная или трансформаторная).
В случае использования нагрузочной цепи с трансформаторной связью частотный коэффициент передачи в области рабочих частот
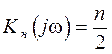 , (2.14)
, (2.14)
где 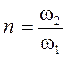 , (2.15)
, (2.15)
w1 и w2 – число витков первичной и вторичной обмоток трансформатора.
2.1.4 Электронные тракты усиления и обработки сигнала
В общем случае частотные передаточные коэффициенты усилительного тракта могут быть весьма сложными и зависящими от функциональной и структурной схем электронного тракта усиления и обработки.
В усилительном тракте приборов контроля можно выделить несколько устройств, которые присутствуют практически во всех приборах НК.
Прежде всего это оптимальный фильтр, функции которого обычно выполняет один или несколько каскадов усилителя.
С точностью до постоянной
 , (2.16)
, (2.16)
где 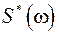 и
и 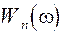 – комплексно сопряженная спектральная плотность полезного сигнала и спектральная плотность мощности помехи на входе в 1-ый каскад усиления соответственно;
– комплексно сопряженная спектральная плотность полезного сигнала и спектральная плотность мощности помехи на входе в 1-ый каскад усиления соответственно;
t0 – время достижения максимума отношением сигнал/шум на выходе фильтра.
На практике часто применяют квазиоптимальные фильтры вместо оптимальных. Это обеспечивает более простую реализацию. Для данных целей используют избирательные усилители.
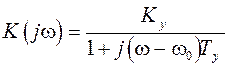 , (2.17)
, (2.17)
где  – коэффициент усиления при w=w0, на которой сосредоточена основная энергия сигнала;
– коэффициент усиления при w=w0, на которой сосредоточена основная энергия сигнала;
Ту – постоянная времени.
Постоянная времени Ту связана с эффективной полосой пропускания соотношением
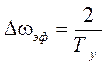 . (2.18)
. (2.18)
В данной полосе
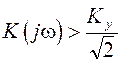 . (2.19)
. (2.19)
Постоянную времени Ту подбирают в соответствии с полосой частоты пропускания.
Усилители мощности чаще всего имеют передаточный коэффициент
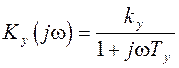 , (2.20)
, (2.20)
где Ту – постоянная времени усилителя.
Спектр сигнала на входе можно найти, предварительно получив модель входного сигнала во временной области. Далее необходимо воспользоваться
преобразованием Фурье и в зависимости от характера сигнала (детерминированный или случайный) найти спектральную плотность этого сигнала.
Если S(t) – модель детерминированного сигнала во временной области, то спектр сигнала
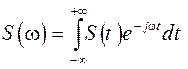 . (2.21)
. (2.21)
При расчете спектра пачки импульсов, следующих на объект контроля, можно воспользоваться свойствами преобразований Фурье, а потом свернуть полученное выражение по формуле суммы членов прогрессии. Для определения числа импульсов N, падающих на объект, следует задаться временем контроля tk, принимая во внимание характеристики производительности контроля.
Расчет спектра сигнала на выходе устройства необходимо производить в соответствии с методикой расчета сигналов при прохождении ими линейных цепей. При этом следует обращать внимание на характер сигнала, проходящего через эту цепь.
Для входного и выходного сигналов построить график спектральной плотности (спектра мощности) можно путем расчета ее значения на фиксированной частоте и последующем ее изменении с повторением расчета. Для расчета удобно использовать ЭВМ, а результаты расчета представить на миллиметровке.
При расчете значений действующих шумов в первую очередь необходимо определить доминирующие шумы. В соответствии с видом шума записать его спектр мощности, а потом привести все шумы к одной точке схемы преобразования сигналов. Общее значение шума в данной точке можно находить в предположении, что все шумы независимы.
До поступления в оптимальный фильтр системы обнаружения полезный сигнал проходит через фотоприемник, нагрузочную цепь и предварительный усилитель. Спектр полезного сигнала на входе в оптимальный фильтр составит
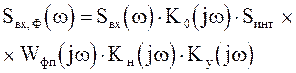 . (2.22)
. (2.22)
Спектральная плотность входного сигнала Sвх(w) определяется видом используемого источника излучения (точечный, протяженный и др.) и зависит прежде всего от площади входного зрачка или углового поля зрения прибора.
Найдем теперь уравнение, связывающее спектральную плотность мощности помех Wвх,Ф(w) на входе в оптимальный фильтр с параметрами оптической системы.
Внешние помехи обычно зависят от параметров оптической системы и обусловлены, как правило, радиационным и фотонным шумами. Радиационные и фотонные шумы возникают вследствие статистического характера потока излучения, представляющего случайную совокупность потока квантов энергии электромагнитного поля.
Радиационные и фотонные внешние помехи при частотах менее 1010 Гц можно считать белыми шумами, мощность которых постоянна во всей области рассматриваемых частот.
Спектральная плотность мощности радиационных и фотонных помех, приведенных ко входу в оптимальный фильтр, определяется выражением, справедливым для обоих случаев:
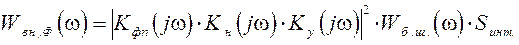 (2.23)
(2.23)
К внутренним шумам, зависящим от параметров оптической системы, относятся шумы, генерируемые в самих фотоприемниках и зависящие от протекающего в них тока. К ним относятся дробовые, токовые и генерационно-рекомбинационные шумы. Сюда же относятся тепловые шумы. Состав и количественные параметры спектральных плотностей мощности этих шумов зависят от типа применяемого фотоприемника. В общем виде спектральные плотности мощности перечисленных составляющих шумов представляются в виде:
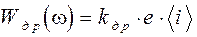 ; (2.24)
; (2.24)
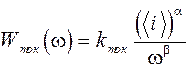 ; (2.25)
; (2.25)
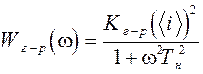 ; (2.26)
; (2.26)
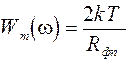 , (2.27)
, (2.27)
где <i> – среднее значение силы тока, протекающего через ФП;
e=1,6.10-19 Кл – заряд электрона;
k – постоянная Больцмана (1,38.10-23 Дж/к);
Т – температура фотоприемника, °К;
Тн – среднее время жизни носителей заряда в полупроводниковых ФП;
Rфп – внутреннее сопротивление теплового ФП, Ом;
a=2;
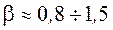 ;
;
kдр, kток, kг-р – коэффициенты, зависящие от конкретных образцов ФП, которые, как правило, определяются экспериментально.
Спектральная плотность мощности шумов ФП, приведенная ко входу оптимального фильтра, составляет
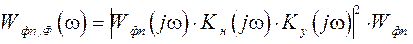 , (2.28)
, (2.28)
где
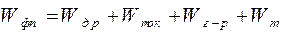 . (2.29)
. (2.29)
К внутренним помехам, не зависящим от параметров оптики, относятся шумы, генерируемые активными сопротивлениями нагрузочной цепи, и в элементах электронного тракта усилителя. При этом достаточным бывает учитывать шумы, генерируемые в первом каскаде усилительного тракта. Именно здесь полезный сигнал имеет еще малые значения по сравнению с генерируемыми шумами. На входе в усилитель шумы нагрузочной цепи и первого каскада усилителя представляются в виде:
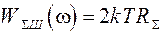 , (2.30)
, (2.30)
где RS – суммарное эквивалентное шумовое сопротивление элементов нагрузочной цепи и первого каскада усилителя;
Т – температура элементов электронного тракта (Т=300°К).
Спектральная плотность мощности этих помех, приведенных ко входу в оптимальный фильтр,
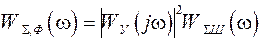 . (2.31)
. (2.31)
Таким образом, определены все составляющие помехи и приведены ко входу оптимального фильтра. Тогда
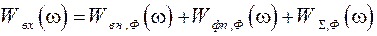 . (2.32)
. (2.32)
Расчет необходимого соотношения сигнал/шум и порогового уровня принятия решения необходимо производить в зависимости от вида исходных данных: допустимого значения вероятности ложной тревоги, средней частоты или среднего периода появления ложной тревоги или вероятности появления хотя бы одной ложной тревоги за определенное время наблюдения. При этом будет найден пороговый уровень принятия решения о наличии дефекта. Увеличивать вероятность правильного обнаружения дефекта можно за счет выбора значения соотношения сигнал/шум большего, чем пороговое значение. В этом случае необходимо рассчитать вероятность правильного обнаружения, пользуясь таблицей интеграла вероятности.
Допустимые параметры ложных тревог могут быть заданы тремя способами:
1) допустимым значением вероятности ложной тревоги Рл.т.;
2) средней частотой 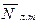 или средним периодом
или средним периодом 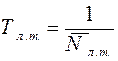 появления ложной тревоги;
появления ложной тревоги;
3) вероятностью появления хотя бы одной ложной тревоги за время наблюдения Тн (обычно используется при редких ложных тревогах).
Если задано значение вероятности ложной тревоги Рл.т., то рассчитывается величина
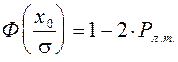 , (2.33)
, (2.33)
где Х0 – пороговое значение сигнала; s2 – дисперсия действующего шума.
По таблицам интеграла вероятности 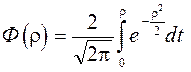 находится относительный порог
находится относительный порог 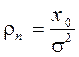 , который и устанавливает необходимое значение сигнал/шум на выходе устройства обнаружения. Он называется параметром обнаружения.
, который и устанавливает необходимое значение сигнал/шум на выходе устройства обнаружения. Он называется параметром обнаружения.
Если дисперсия шума s2 на выходе фильтра известна, то пороговое значение сигнала 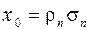 .
.
Вероятность правильного обнаружения в случае, когда отношение сигнал/шум на выходе фильтра превышает величину параметра обнаружения, может быть найдена по формуле
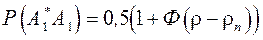 . (2.34)
. (2.34)
Если задана средняя частота появления ложных тревог, то для расчета требуемого порогового отношения сигнал/шум пользуются формулой
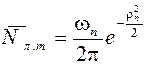 , (2.35)
, (2.35)
где wп – средняя квадратичная круговая частота пересечения помехой на выходе фильтра нулевого уровня.
В случае установки перед пороговым устройством оптимального фильтра величина wп определяется следующим образом:
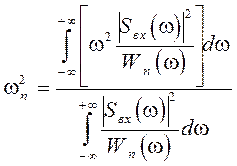 , (2.36)
, (2.36)
где Sвх(w) – спектральная плотность сигнала;
Wп(w) – спектр мощности действующего шума.
В тех случаях, когда перед пороговым устройством установлен фильтр нижних частот с частотным коэффициентом передачи показанным на рисунке 2.2, величина wп рассчитывается так:
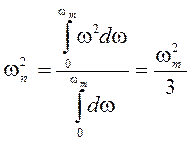 . (2.37)
. (2.37)
Для полосового и избирательного фильтров, передаточные характеристики которых показаны на рисунке 2.3 и рисунке 2.4 соответственно, эта величина с достаточной степенью точности определяется так:
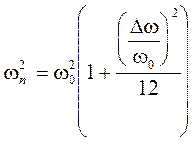 , (2.38)
, (2.38)
где w0 – средина полосы пропускания.
 Рисунок 2.2 – Передаточная характеристика фильтра низких частот Рисунок 2.2 – Передаточная характеристика фильтра низких частот | 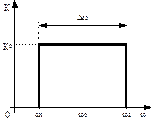 Рисунок 2.3 – Передаточная характеристика полосового фильтра Рисунок 2.3 – Передаточная характеристика полосового фильтра |  Рисунок 2.4 – Передаточная характеристика избирательного усилителя Рисунок 2.4 – Передаточная характеристика избирательного усилителя |
Из формулы (2.35) следует, что
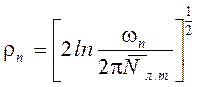 . (2.39)
. (2.39)
Если задана допустимая вероятность появления 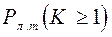 хотя бы одной ложной тревоги за определенное время наблюдения Тн, то для расчета необходимого порогового соотношения сигнал/шум используют формулу:
хотя бы одной ложной тревоги за определенное время наблюдения Тн, то для расчета необходимого порогового соотношения сигнал/шум используют формулу:
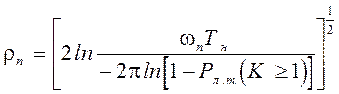 . (2.40)
. (2.40)
Для расчета параметров устройства обработки следует составить основное энергетическое уравнение, которое затем решить относительно неизвестной величины. Если существенных параметров устройства два и более, то решением уравнения служит связь между этими параметрами. Задаваясь приемлемым значением одного или нескольких находят остальные.
Основное энергетическое уравнение имеет вид:
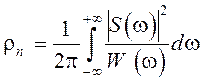 . (2.41)
. (2.41)
Часто полезным является применение теоремы Парсеваля, которая следует из формулы Рэлея. Она определяет равенство энергий сигналов при их представлении в частотной и временной областях.
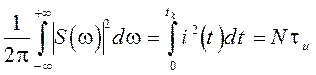 , (2.42)
, (2.42)
где tk – время контроля;
N – число импульсов;
tи – длительность импульса.
В этом случае предполагается, что зондирующие импульсы имеют единичную амплитуду.
Расчет информационного содержания непрерывного сигнала может быть произведен в предположении, что функция распределения плотности вероятностей соответствует нормальному закону распределения. При количественной оценке информационного содержания дискретных сигналов следует обращать внимание на количество уровней и число этих сигналов.
Если на устройство контроля следует информационный сигнал Х вместе с помехой Y, то количество информации I, получаемое приемником в этих условиях можно определить по формуле:
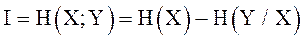 , (2.43)
, (2.43)
где Н(Х) – энтропия полезного сигнала;
Н(Y) – условная энтропия.
Поскольку решающее устройство фиксирует факт наличия или отсутствия сигнала, то имеем
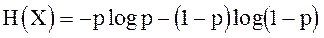 , (2.44)
, (2.44)
где р – вероятность правильного обнаружения сигнала.
При расчете коэффициента полезного действия необходимо учесть потери сигнала в оптической системе, потери при модуляции, если она имеется, и потери из-за несогласованности характеристик тракта, а также коэффициент полезного действия электронного тракта усиления и обработки.
Коэффициент полезного действия (КПД) определяет, какая доля полезного сигнала, поступающего на вход прибора, используется для создания выходного сигнала. КПД зависит от ряда факторов. Важнейшими из них являются потери потока в оптической системе, потери при модуляции и обработке, потери из-за отсутствия надлежащего согласования параметров приемника с параметрами оптической и электронной систем. В результате можно записать
 , (2.45)
, (2.45)
где h0 – часть потерь в оптической системе;
kм – часть потерь при модуляции;
hсг – часть потерь из-за несогласованности характеристик.
Для пассивных систем
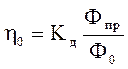 , (2.46)
, (2.46)
где Фпр – световой поток фотоприемника;
Фо – световой поток, упавший на оптическую систему;
Кд – коэффициент диафрагмирования.
Коэффициент Км учитывает потери излучения при модуляции прерыванием и потери излучения за счет изменения спектра.
Для различного вида модуляции коэффициент Км различен. Так:
–для прямоугольных импульсов, промодулированных синусоидальной функцией, Км=0,16;
–для прямоугольных импульсов, промодулированных прямоугольной функцией, Км=0,2.
Коэффициент hсг учитывает возможные несоответствия между площадью чувствительного слоя ФП и площадью сечения пучка в месте
установки этого слоя Аф. При разработке систем обнаружения дефектов стремятся, чтобы размер площади чувствительного слоя был больше, чем площадь пучка излучения.
Другой составляющей является коэффициент Кш , учитывающий соотношение между шумом электронной системы, приведенным к приемнику, и собственным шумом приемника:
 , (2.47)
, (2.47)
где Uш,пр – шум приемника;
Uшэ – шум электронной системы.
Коэффициент hсг учитывает и тот факт, что при выполнении модуляции на рабочей частоте уровень шума может отличаться от паспортного значения. Это получается за счет того, что модуляция производится на частоте, отличной от частоты паспортизации.
Список литературы
1. Якушенков Ю.Г. Теория и расчет оптико-электронных приборов: Учебник для ВУЗов.– 3-е изд. доп. и перераб.– М.: Машиностроение, 1989.
2. Порфирьев Л.Ф. Основы теории преобразования сигналов в оптико-электронных системах: Учебник для ВУЗов.– Л.: Машиностроение, 1989.
3. Парулюсов Ю.Б., Солдатов В.П., Якушенков Ю.Г. Проектирование оптико-электронных приборов / Под общ. ред. Ю.Г.Якушенкова.– М.: Машиностроение, 1990.
4. Баскаков С.И. Радиотехнические цепи и сигналы. Уч. пособие.– 2-е изд. перераб. и доп.– М.: Высшая школа, 1988.
5. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники.– М.: Энергия, 1979.
6. Тихонов В.И. Оптимальный прием сигналов.– М.: Радио и связь, 1983.
7. Ишанин Г.Г. Приемники излучения оптических и оптико-электронных приборов.– Л.: Машиностроение, 1986.
8. Мирошников М.М. Теоретические основы оптико-электронных приборов.– Л.: Машиностроение, 1983.
9. Якушенков Ю.Г., Луканцев В.Н., Колосов М.П. Методы борьбы с помехами в оптико-электронных приборах.– М.: Радио и связь, 1981.
