Доказательства утверждений

УТВ О - 2 Свойства обратного отображения

2.1 Обратимость отображения эквивалентна его биективности: (A:X®Y обратимо, т.е. $ обратное о. A^-1:Y®X) Û (A:X®Y биективно, т.е. одновременно сюръективно и инъективно).

Д-во. Þ?$ обратное о. A^-1:Y®X Þ A:X®Y биективно ?

1) Ax₁ = Ax₂ =(действуем на равенство отображением A^-1, существующим в силу условия теоремы)Þ A^-1(Ax₁) = A^-1(Ax₂) =(определение композиции А^-1А)Þ A^-1Ax₁ = A^-1Ax₂
=(А^-1А=1_X)Þ x₁=x₂ =[эквивалентное определение инъективности: (Ax₁ = Ax₂ Þ x₁=x₂) Û x₁¹x₂ Þ Ax₁ ¹ Ax₂)]Þ А инъективное о.!

2) "yÎY =(A^-1:Y®X)Þ x = A^-1yÎX =(действуем на равенство отображением А)Þ
Аx = А(A^-1y) =(определение композиции АA^-1)Þ Аx = АA^-1y =(АA^-1 = 1_Y)Þ Аx = yÜ(определение м. всех значений, imA)Þ imA = A(X) = YÜ(определение сюръективного о.)Þ А сюръективное о.!

Таким образом, из 1) и 2) вытекает биективность А!

Ü? A:X®Y биективно Þ $ обратное о. A^-1:Y®X ?

Задаем претендента из объема понятия отношение в YÈX:

A^-1 = {<y,x>ÎY´X | <x,y>ÎA}ÍY´X,

т.е. x = A^-1y Û y = Ax, и проверяем видовые признаки более узкого понятия
обратное о. A^-1:Y®X:

1° A^-1 – отображение из Y в X ? (A^-1:D(A^-1)ÍY®X ?)

2° D(A^-1) = Y ? (A^-1:Y®X ?)

3° А^-1А=1_X & АA^-1 = 1_Y ? (т.е.А^-1 действительно обратное отображение для А ?).

1° Ü(определение отображения из)Þ x = A^-1y & x¢ = A^-1y =(?)Þ x=x¢.

x = A^-1y & x¢ = A^-1y Ü(определение отношения А^-1)Þ y = Ax & y = Ax¢ =(симметричность и транзитивность отношения =_Y)Þ Ax=Ax¢ =(A инъективен)Þ x=x¢!

2° Ü(определение равенства множеств)Þ D(A^-1)ÍY & YÍ D(A^-1) ? Ü(определение D(A^-1) = {yÎY | $xÎX : x=A^-1y}ÍY)Þ YÍ D(A^-1) ? Ü(определение подмножества)Þ yÎY Þ yÎ D(A^-1) ?

yÎY =(А сюръективно)Þ $xÎX | y = Ax Ü(определение отношения А^-1)Þ $xÎX | x = A^-1y =(определение D(A^-1))Þ yÎ D(A^-1)!

3° Ü(определения равенства отображений и тождественного отображения)Þ

3.1. xÎX =(?)Þ x = A^-1Ax

3.2. yÎY =(?)Þ y = AA^-1y

xÎX =( A:X®Y)Þ y =AxÎY Ü(определение А^-1)Þ y =Ax & x = A^-1y =(подставляем
y = Ax во второе равенство)Þ x = A^-1Ax !

yÎY =( A^-1:Y®X)Þ x = A^-1yÎX Ü(определение А^-1)Þ y =Ax & x = A^-1y =(подставляем
x = A^-1y в первое равенство)Þ y = AA^-1y !

1°,2°,3° доказаны ¨

Задачи для самостоятельной работы

1. Пусть A, B, C – отображения. Доказать утверждение.

Варианты

1. Композиция ассоциативна: (АВ)С = А(ВС).

2. Композиция сюръективных отображений сюръективна.

3. Композиция инъективных отображений инъективна.

4. Композиция биективных отображений биективна.

5. Отображение, обратное к данному, единственно.

6. Композиция обратимых отображений обратима и (ВА)^-1 = А^-1 В ^–1.

7. S[a, b] É B[a, b] É C[a,b] É C^k[a,b] É С^∞ [a,b] (доказать одно, любое, включение).

8. 1 < p < q Þ l₁ Ì l_p Ì l_q Ì l_∞ Ì l (доказать одно, любое, включение).

9. А инъективен Û Уравнение Ax = yне может иметь более одного решения"yÎY.

10. А сюръективен Û Уравнение Ax = yимеет решение при "yÎY.

11. А биективен Û Уравнение Ax = yпри "yÎY имеет единственное решение, которое может быть найдено по формуле x = A^-1y, где A^-1- обратный оператор.

12. Композиция отображений является отображением.

Образец решения (1 задача). Композиция ассоциативна: (АВ)С = А(ВС).

Д-во. "x (AB)Cx=(определение композиции С и АВ)= АВ[С(х)] =( определение композиции В и А)= A(B[C(x)]) =(определение композиции С и В)= A(BC(x)) =(определение композиции BС и А)= A(BC)x=(по определению поточечного равенства отображений)Þ (АВ)С = А(ВС) §

2. Даны два (несколько) отображения. Найти значение композиции отображений на данном аргументе.

Варианты.

1. X=l₂; Ax = {x₃,x₄,…}:X®X; Bx = Fx = x₁ + x₂ :X®R;
x₀ = . FABx₀ = ? (Ответ: )

2. X=C[0,1]; (Ax)(t) = t²x(t):X®X; (Bx)(t) = Fx =
x₀(t) = t; FABx₀ = ? (Ответ: )

3. X=C[0,1]; (Ax)(t) = x(t²):X®X; (Bx)(t) = x²(t):X®X; Fx = x₀(t) = FABx₀ = ? (Ответ: )

4. X=Ã([0,2]); Ax = xÇ[0,1]:X®X; Bx = [0,2]\x:X®X; Fx = sup x :X®R; x₀ = {0,1,2}; FABx₀ = ? (Ответ: 1)

3. Решите "свой" вариант теста (не забудьте указать вариант, например, ТЕСТ О - 1). Тестовое задание (ТЗ) с номером № студента (mod12) представьте с решением, на остальные ТЗ пришлите только ответы.

Варианты

1. ТЕСТ О - 1.

№	А	В	Дополнительная информация
	ОтображениеI(x) = x	ОтображениеА|x1 ¹ x2 Þ Ax1¹Ax2	Понятия
	Биективное о.	Обратимое о.	Понятия
	Функц-алFx =	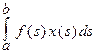ФункционалFx = x(0)	Понятия
	Ф. п. Í S[a,b], состоящее из непрерывных функций	Ф.п. бесконечно дифф-мых функций, С¥[a,b]	Понятия
	Правая часть уравнения	Элементx Î X , при котором высказывание Ах = у истинно	Понятия
	Lp[a,b]	L1[a,b]	Множества, p>1
	C3[a,b]	C2[a,b]	Множества, a<b
	a(t) < 0 "t	A-1a = A1/a	Пар. выс-я, aÎS(T,R)
	А биективен	Уравнение Ax = yимеет единственное решение	Пар-е выск-я, Ax = y
	ABсюръективен	А сюръективен	Пар-е выск-я, A,BÎS(X)
	Bсюръективен	BA сюръективен	Пар-е выск-я, A,BÎS(X)
	A- биекция	A сюръективен	Пар-е выск-я, AÎS(X)

2. ТЕСТ О - 2.

№	А	В	Дополнительная информация
	ОтношениеR Í C´U	ОтображениеА: A(X) = Y	Понятия
	Сужение о. А на подмножество U, Aú U	ОтображениеAú U Î S(U,Y): Aú U (x) = A(x) " x Î X	Понятия, AÎS(X,Y) U Í X
	ОператорAx = dx/dt	Множество (м.)	Понятия
	Ф. п. ÍS[a,b], состоящее из k раз непрерывно дифференцируемых функций	Ф. п. Í S[a,b], состоящее из непрерывных функций	Понятия
	Ф. п. ÍS[a,b], состоящее из суммируемых функций (т.е. < ¥)	Подмножествов S(X,Y)	Понятия
	Элемент S(P, PR)	Уравнение, Ax = y	Понятия
	B[a,b]	C[a,b]	Множества, a<b
	A-1a = A1/a	a(t) > 0 "t	Пар-е выск-я, aÎS(T,R)
	xÎC[-1, 1]	xÎC1[-1, 1]	Выс-я, x(t)=|t|
	Уравнение Ax = yимеет решение	А сюръективен	Пар-е выск-я, Ax = y
	A инъективен	BAинъективно	Пар-е выск-я, A,BÎS(X)
	A- биекция	A инъективен	Пар-е выск-я, AÎS(X)

3. ТЕСТ О - 3.

№	А	В	Дополнительная информация
	Инъективное о.	О.А | Ax1 = Ax2 Þ x1 = x2	Понятия
	Биективное о.	ОтображениеA, которое одновременно инъективно и сюръективно	Понятия
	График о.	Дифференциальный о.	Понятия
	Ф. п. Í S[a,b], состоящее из непрерывных функций	Ф.п. ограниченных на отрезке функций, B[a,b]	Понятия
	Ф.п. суммируемых на отрезке функций, L1[a,b]	Ф. п. ÍS[a,b], состоящее из суммируемых в p-й степени функций (т.е. таких x, что p<¥)	Понятия
	lq	lp	Множества, p<q
	FABx, x(t) º 1	FBAy, y(t) º 1	Числа, Bx(t)=tx(t), Ax(t)=ò[0,1]tsx(s)ds, Fx = x(1)
	A инъективен	Ур-е Ах=y не может иметь более 1 решения	Пар-е выск-я, Ax = y
	Уравнение Ax = yимеет решение	А сюръективен	Пар-е выск-я, Ax = y
	ABинъективно	Винъективен	Пар-е выск-я, A,BÎS(X)
	ABсюръективен	А сюръективен	Пар-е выск-я, A,BÎS(X)
	A инъективен и сюръективен	A- биекция	Пар-е выск-я, AÎS(X)

4. ТЕСТ О - 4.

№	А	В	Дополнительная информация
	Обратимое о.	Обратное о., А-1	Понятия
	Биективное о.	О.А | x1 ¹ x2 Þ Ax1 ¹ Ax2	Понятия
	О.А, для которого X и Y - ф.п.	ОтображениеА, для которого X - функциональное пространство, а Р- числовое поле	Понятия
	Оператор(Ax)(t) = =ò[a,b]k(t,s)x(s)ds, t Î [c,d]	Интегральный оператор	Понятия
	Подмножествов S(X,Y)	Ф. п. Í S[a,b], состоящее из ограниченных функций	Понятия
	Ф. п. ÍS[a,b], состоящее из суммируемых функций (т.е. < ¥)	Подмножествов S(X,Y)	Понятия
	lp	l1	Множества, p>1
	FABx, x(t) = t	FBAy, y(t) = t2	Числа, Bx(t)=tx(t),Ax(t)=ò[0,1]tsx(s)ds, Fx = x(1)
	a(t) < 0 "t	A-1a = A1/a	Пар. выс-я, aÎS(T,R)
	xÎC2[0, 2]	xÎB[0, +¥)	Выс-я, x(t)=|t|
	x = A-1y	А сюръективен	Пар-е выск-я, Ax = y
	ABсюръективен	Aи B сюръективны	Пар-е выск-я, A,BÎS(X)

5. ТЕСТ О - 5.

№	А	В	Дополнительная информация
	ОтображениеА, для которого существует обратное о.	О. изA:DA Í X®Y ½ DA = X	Понятия
	ОтображениеAú U Î S(U,Y): Aú U (x) = A(x) " x Î U	Сужение о. А на подмножество U, Aú U	Понятия
	ОператорA аÎ S(X): (Ааx) (t) = a(t) x(t)	О.А, для которого X и Y - ф.п.	Понятия
	Функциональное пространство	Подмножествов S(X,Y)	Понятия
	Ф. п. Íl, состоящее из ограниченных последовательностей (т.е. таких x = {xk }Î l, что sup{ôxkô} < ¥)	Ф.п. ограниченных последовательностей, l¥	Понятия
	Элементy Î Y	Подсистема	Понятия
	C[a,b]	S[a,b]	Множества, a<b
	FABx, x(t) = t	FBAy, y(t) = t2	Числа, Bx(t)=tx(t), Ax(t)=ò[0,1]tsx(s)ds, Fx = x(1)
	a(t) < 0 "t	A-1a = A1/a	Пар. выс-я, aÎS(T,R)
	xÎC[-1, 1]	xÎC1[-1, 1]	Выс-я, x(t)=|t|
	x = A-1y	А биективен	Пар-е выск-я, Ax = y
	Aи Bинъективны	ABинъективен	Пар-е выск-я, A,BÎS(X)

6. ТЕСТ О - 6.

№	А	В	Дополнительная информация
	Композиция отображений А и В, ВА	ОтображениеВА(х) = В(А(х))	Понятия, AÎS(X,Y), BÎS(Y,Z)
	ОтображениеA, которое одновременно инъективно и сюръективно	Обратимое о.	Понятия
	Функция	ОтображениеAÎ S(X,R)	Понятия
	d - функция Дирака	Интегральный функционал	Понятия
	Ф. п. Íl, состоящее из суммируемых последовательностей x = ={xk}Î l | å1,¥|xk|< ¥	Ф. п. Íl, состоящее из последовательностей с суммируемой p-й степенью (т.е. таких x = {xk}Î l, что å1,¥|xk|p < ¥)	Понятия
	Ф.п. суммируемых на отрезке функций, L1[a,b]	Ф. п. ÍS[a,b], состоящее из суммируемых в p-й степени функций (т.е. таких x, что p<¥)	Понятия
	Элементy Î Y	Элементx Î X , при котором высказывание Ах = у истинно	Понятия
	S[a,b]	C¥[a,b]	Множества, a<b
	xÎl2	xÎl¥	Выс-я, x={xk=1}
	А биективен	Уравнение Ax = yимеет единственное решение	Пар-е выск-я, Ax = y
	x = A-1y	А сюръективен	Пар-е выск-я, Ax = y
	Bсюръективен	BA сюръективен	Пар-е выск-я, A,BÎS(X)

ã Калмыков А.А. 2005. m_o.doc