Поставим задачу: построить для произвольной булевой функции минимальные ДНФ. 2 страница
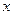 |  | 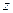 |  |
б) 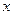 :
: 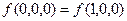 ,
, 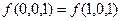 ,
,
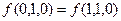 ,
, 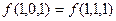 , следовательно,
, следовательно, 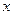 - фиктивная.
- фиктивная.
 :
: 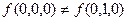 , следовательно,
, следовательно,  - существенная.
- существенная.
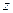 :
: 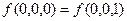 ,
, 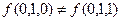 , следовательно,
, следовательно, 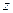 - существенная.
- существенная.
в) решить самостоятельно.►
Операция удаления (введения) фиктивных переменных. Пусть для функции 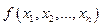 переменная
переменная 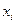 является фиктивной. Возьмем таблицу истинности функции
является фиктивной. Возьмем таблицу истинности функции  . Вычеркнем из нее все строки, в которых
. Вычеркнем из нее все строки, в которых 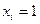 , а также вычеркнем столбец переменной
, а также вычеркнем столбец переменной 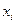 . Полученная таким образом таблица будет задавать некоторую функцию
. Полученная таким образом таблица будет задавать некоторую функцию 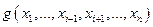 , причем на любом наборе
, причем на любом наборе 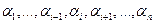 значений переменных
значений переменных 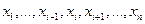 для функций
для функций  и
и 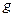 выполнено равенство
выполнено равенство 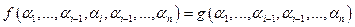 . Про функцию
. Про функцию 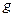 говорят, что она получена из функции
говорят, что она получена из функции  путем удаления фиктивной переменной, а про функцию
путем удаления фиктивной переменной, а про функцию  говорят, что она получена из
говорят, что она получена из 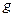 путем введения фиктивной переменной.
путем введения фиктивной переменной.
Определение. Функции  и
и 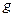 называются равными, если функцию
называются равными, если функцию 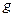 можно получить из функции
можно получить из функции  путем введения или удаления фиктивных аргументов.
путем введения или удаления фиктивных аргументов.
Упражнение 2.8.Найти функции, равные данным и существенно зависящие от всех своих аргументов:
а) 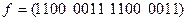 ; б)
; б) 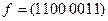 .
.
| v | 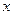 |  | 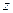 | 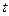 |  |
◄ а)Сначала выясним, какие из аргументов функции  фиктивные. Для удобства рассуждений дополним таблицу истинности функции столбцом номеров булевых векторов.
фиктивные. Для удобства рассуждений дополним таблицу истинности функции столбцом номеров булевых векторов.
Чтобы выяснить, является переменная 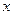 фиктивной или существенной, нужно сравнить значения функции на парах векторов, отличающихся лишь значениями переменной
фиктивной или существенной, нужно сравнить значения функции на парах векторов, отличающихся лишь значениями переменной 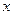 . Такие пары образуют вектора с номерами 0 и 8, 1 и 9, 2 и 10, …, 7 и 15. Так как сравниваемые значения одинаковы, переменная
. Такие пары образуют вектора с номерами 0 и 8, 1 и 9, 2 и 10, …, 7 и 15. Так как сравниваемые значения одинаковы, переменная 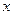 фиктивная.
фиктивная.
Теперь сравниваем значения функции на парах векторов, отличающихся лишь значениями переменной  (эти вектора имеют номера 0 и 4, 1 и 5, 2 и 6, 3 и 7, 8 и 12,…, 11 и 15). Имеем
(эти вектора имеют номера 0 и 4, 1 и 5, 2 и 6, 3 и 7, 8 и 12,…, 11 и 15). Имеем 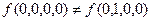 , следовательно,
, следовательно,  - существенная переменная.
- существенная переменная.
Сравниваем значения функции на парах векторов, отличающихся лишь значениями переменной 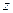 (эти вектора имеют номера 0 и 2, 1 и 3, 4 и 6, 5 и 7, …, 13 и 15). Имеем
(эти вектора имеют номера 0 и 2, 1 и 3, 4 и 6, 5 и 7, …, 13 и 15). Имеем 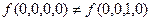 , следовательно,
, следовательно, 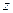 - существенная переменная.
- существенная переменная.
 | 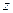 | 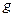 |
И наконец, сравниваем значения функции на парах векторов, отличающихся лишь значениями переменной 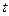 ( они имеют номера 0 и 1, 2 и 3, 4 и 5, …, 14 и 15). Поскольку сравниваемые значения одинаковы, то переменная
( они имеют номера 0 и 1, 2 и 3, 4 и 5, …, 14 и 15). Поскольку сравниваемые значения одинаковы, то переменная 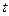 - фиктивная.
- фиктивная.
Вычеркиваем из таблицы истинности функции 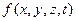 строки и столбцы, закрашенные серым цветом, получаем таблицу истинности для функции
строки и столбцы, закрашенные серым цветом, получаем таблицу истинности для функции 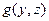 . Функции
. Функции  и
и 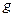 равны, и функция
равны, и функция 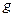 - существенно зависит от всех своих аргументов.
- существенно зависит от всех своих аргументов.
б) решить самостоятельно.►
Замечания. 1.Далее, если число переменных специально не оговаривается, функции рассматриваются с точностью до фиктивных переменных, т.е. предполагается, что с заданием некоторой функции  заданы все равные ей функции, и для обозначения равных функций используется один и тот же функциональный символ.
заданы все равные ей функции, и для обозначения равных функций используется один и тот же функциональный символ.
2. В дальнейшем при рассмотрении любой системы функций предполагается (если не оговорено противное), что все функции данной системы зависят от одного числа переменных. Такой подход позволяет избежать громоздких рассуждений.
2.1.2. Реализация булевых функций формулами
Для задания булевых функций помимо таблиц также используют формулы. Формулы обычно строят по «принципу матрешек», вкладывая друг в друга символические записи элементарных функций. Говоря о формуле, часто указывают, с использованием каких функций она строилась. Например, 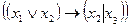 - это формула над множеством, состоящим из дизъюнкции, импликации и штриха Шеффера, а
- это формула над множеством, состоящим из дизъюнкции, импликации и штриха Шеффера, а 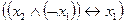 - формула над множеством, состоящим из конъюнкции, отрицания и эквивалентности.
- формула над множеством, состоящим из конъюнкции, отрицания и эквивалентности.
Каждой формуле сопоставляется функция (при этом говорят, что формула реализует функцию). Процедура сопоставления пошаговая. Покажем, как действовать, на примерах.
Упражнение 2.9.Построить таблицу истинности и выписать вектор значений функции:
а) 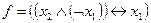 ; б)
; б) 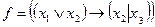 ; в)
; в) 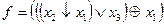 .
.
◄ а)
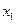 | 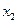 | 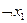 | 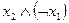 | 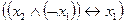 |
Вектор значений функции 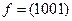 .
.
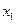 | 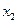 | 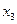 | 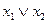 | 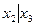 | 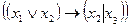 |
б)
Вектор значений функции 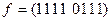 .
.
в)решить самостоятельно.►
Итак, на примерах мы рассмотрели понятие формулы над множеством функций 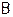 и понятие функции, реализуемой формулой над
и понятие функции, реализуемой формулой над 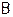 . Теперь этим понятиям нужно дать формальные определения.
. Теперь этим понятиям нужно дать формальные определения.
Определение. Пусть 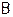 - некоторое подмножество функций из
- некоторое подмножество функций из 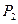 ;
; 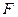 - множество символов, используемых для обозначения функций из множества
- множество символов, используемых для обозначения функций из множества 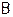 ;
; 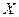 - множество символов, используемых для обозначения переменных;
- множество символов, используемых для обозначения переменных; 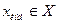 ,
, 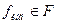 . Тогда
. Тогда
1. каждое выражение вида 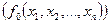 , называется формулой над
, называется формулой над 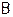 ;
;
2. выражение вида 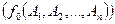 , где
, где 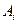 - либо символ переменной
- либо символ переменной 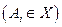 , либо формула над
, либо формула над 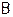 , называется формулой над
, называется формулой над 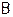 .
.
Обозначения: 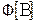 - формула над множеством функций
- формула над множеством функций 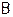 ;
; 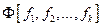 - формула над множеством функций
- формула над множеством функций 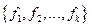 .
.
Определение функции, реализуемой формулой, также строится индуктивно. Оно громоздкое и довольно сложное для восприятия. Мы рассмотрим его несколько позже. Опыт показывает, что при первом знакомстве с курсом вполне достаточно понимать, что такое функция, реализуемая формулой, интуитивно.
Если формула 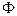 реализует функцию
реализует функцию  , то пишут
, то пишут 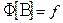 .
.
Функцию  , реализуемую формулой над множеством функций
, реализуемую формулой над множеством функций 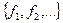 , будем называть суперпозицией функций
, будем называть суперпозицией функций 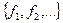 .
.
Замечание. Для упрощения записи формул введен ряд соглашений:
а) внешние скобки у формул можно опускать;
б) вместо 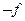 можно писать
можно писать 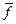 , а вместо
, а вместо 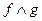 –
– 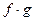 или
или 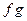 ;
;
в) связку « 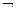 » принято считать сильнее любой двуместной связки, поэтому внешние скобки в выражении, над которым стоит знак « – », можно опускать;
» принято считать сильнее любой двуместной связки, поэтому внешние скобки в выражении, над которым стоит знак « – », можно опускать;
г) связку « 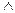 » принято считать сильнее любой другой двуместной связки, поэтому в скобки выражения
» принято считать сильнее любой другой двуместной связки, поэтому в скобки выражения 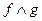 ,
, 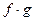 ,
, 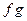 можно не брать.
можно не брать.
Например, формулу 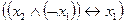 можно записать в виде
можно записать в виде 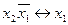 .
.
Упражнение 2.10. Показать, что формулы реализуют равные функции:
а) 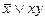 и
и 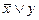 ; б)
; б) 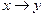 и
и 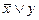 .
.
◄ а)
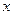 |  | 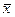 | 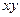 | 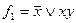 | 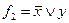 |
б)Выполнить самостоятельно. ►
Если две формулы 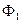 и
и 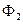 реализуют равные функции, то их называют равносильными и пишут
реализуют равные функции, то их называют равносильными и пишут 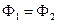 .
.
Теорема. Для формул над множеством 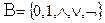 имеют место следующие равносильности:
имеют место следующие равносильности:
1. 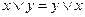 ; 2.
; 2. 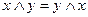 ;
;
3. 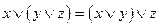 ; 2.
; 2. 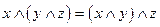 ;
;
5. 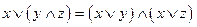 ; 6.
; 6. 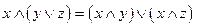 ;
;
7. 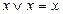 ; 8.
; 8.  ;
;
9. 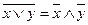 ; 10.
; 10. 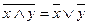 ;
;
11. 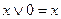 ; 12.
; 12. 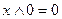 ;
;
13. 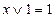 ; 12.
; 12. 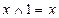 ;
;
15. 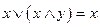 ; 16.
; 16. 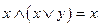 ;
;
17. 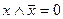 ; 18.
; 18. 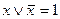 ;
;
19. 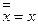 .
.
◄Чтобы доказать справедливость любого из этих равенств, нужно убедиться в равенстве функций, реализуемых формулами, записанными в его левой и правой частях. Для этого достаточно построить таблицы истинности этих функций. Например, для равносильности под номером 10 имеем:
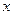 |  | 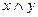 | 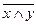 | |
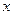 |  | 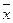 | 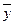 | 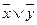 |
Как видим, формулы 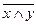 и
и 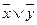 реализуют равные функции и, следовательно, равносильны.
реализуют равные функции и, следовательно, равносильны.
Справедливость остальных равенств проверьте самостоятельно. ►
Равносильности 1-19 характеризуют свойства дизъюнкции, конъюнкции и отрицания: 1 и 2 – коммутативность, 3 и 4 – ассоциативность, 5 – дистрибутивность конъюнкции относительно дизъюнкции, 6 – дистрибутивность дизъюнкции относительно конъюнкции, 7 и 8 – идемпотентность. Равносильности 9 и 10 называют законами де Моргана, 15 и 16 – законами поглощения, 17 – законом противоречия, 18 – законом исключенного третьего, 19 – законом двойного отрицания.
Дополним соглашение об упрощенной записи формул: в случае многократного применения ассоциативной операции скобки можно опускать. Например, формулу 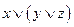 можно записать в виде
можно записать в виде 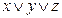 . В дальнейшем будем также употреблять следующие обозначения:
. В дальнейшем будем также употреблять следующие обозначения: 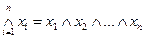 и
и 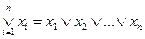 .
.
Упражнение 2.11. Учитывая соглашения о порядке выполнения операций, опустить «лишние» скобки и знак « 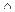 » в формулах:
» в формулах:
а) 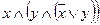 ; б)
; б) 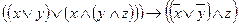 .
.
◄а) 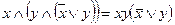 ;
;
б)выполнить самостоятельно.►
Упражнение 2.12. Доказать, что имеет место равносильность:
а) 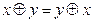 ; б)
; б) 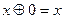 ;
;
в) 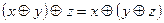 ; г)
; г) 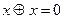 ;
;
д) 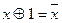 ; е)
; е) 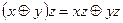 .
.
◄Выполнить самостоятельно.►
Упражнение 2.13. Применяя равносильные преобразования, упростить формулу:
а) 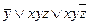 ; б)
; б) 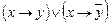 ; в)
; в) 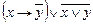 ; г)
; г) 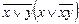 .
.
◄а) 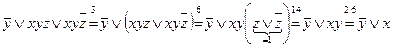 .
.
б) 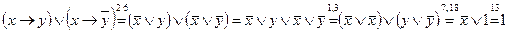 .
.
в)иг)выполнить самостоятельно.►
Упражнение 2.12. Указать существенные и фиктивные переменные функции:
