Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

.

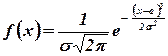Нормальное распределение определяется двумя параметрами: а и s. Можно показать, что а есть математическое ожидание, s - среднее квадратическое отклонение нормального распределения.

Общим называют нормальное распределение с произвольными параметрами а и s (s> 0). Обозначается X ~ N(a, s).Нормированным называют нормальное распределение с параметрами а = 0 и s = 1: X ~ N(0, 1).

Плотность нормированного распределения

.

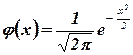Эта функция табулирована.

Функция F(х) общего нормального распределения X ~ N(a, s):

,

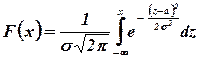а функция нормированного распределения X ~ N(0, 1):

.

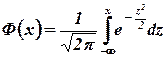Функция Ф(x) табулирована.

Нормальная кривая

График плотности нормального распределения X ~ N(a, s) называют нормальной кривой (кривой Гаусса).

	a

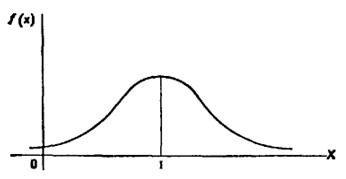
Заметим, что при а = 0 и s = 1 нормальную кривую называют нормированной.

Понятие о теореме Ляпунова. Формулировка

Центральной предельной теоремы

Известно, что нормально распределенные случайные величины широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А. М. Ляпуновым (центральная предельная теорема): если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

Оценка отклонения теоретического распределения от нормального.

Асимметрия и эксцесс

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности асимметрию и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

,

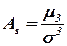где .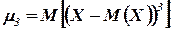

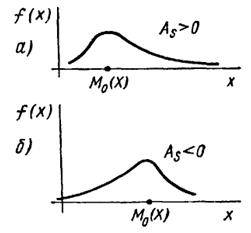Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна (рис. 10, а), если слева — отрицательна (рис. 10, б).

Для оценки «крутости», т. е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой — эксцессом.

Эксцессом теоретического распределения называют характеристику, которая определяется равенством

,

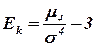где .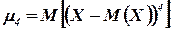

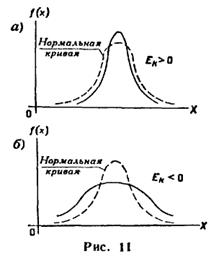
Для нормального распределения 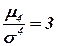; следовательно, эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая (рис. 11, а); если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая (рис. 11,б). При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.