Графоаналитический метод силового анализа механизма

Для расчетного положения механизма необходимо определить все силы и моменты сил, действующие на звенья механизма.

1.Силы тяжести

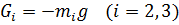
2.Силы от действия горизонтальной и вертикальной перегрузок:

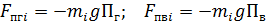
3. Главные векторы и главные моменты инерционных сил, к которым приводятся силы инерции, действующие на каждое звено механизма. Для звеньев 2 и 3

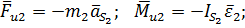
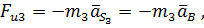
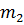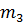где и – массы звеньев 2 и 3; 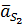и 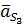– ускорения центров масс звеньев (для звена 3 точка 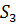совпадает с точкой В); 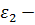угловое ускорение звена 2; 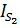– момент инерции масс звена 2 относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена, который определяестя по формуле

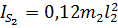
4. Сила трения на ползуне

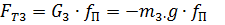
5.Сила сопротивления на ползуне:

для нерабочего хода ползуна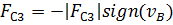

где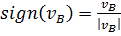

Здесь 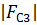– модуль силы сопротивления, соответствующей расчетному положению механизма. Для определения значения этой силы необходимо постоить приближенный график параболической зависимости силы сопротивления от координаты точки В 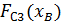, используя три значения функции 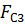для трех значений аргумента 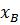, данные в задании.

График зависимости 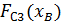представлен на рис. 3.1.

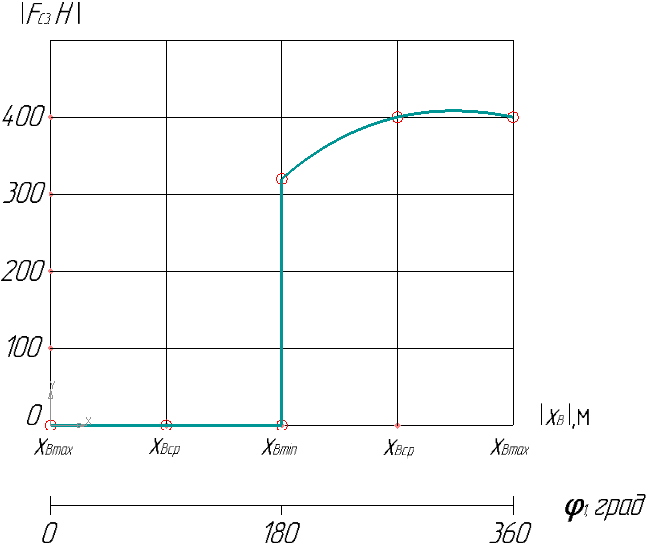
Рис. 3.1. Зависимость силы сопротивления от положения ползуна

Знак «минус» везде учитывает направление силовго параметра, противоположное направлению соответствующего кинематического параметра.

Численное значения сил и моментов сил для расчетного положения рассматриваемого механизма 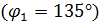будут следующими:

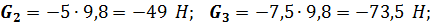
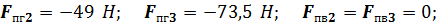
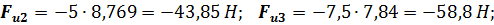
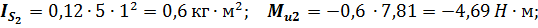
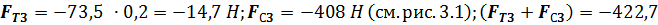
Малыми величинами, которые составляют не более (5...10)% от максимально известной силы, можно пренебречь.

Силовой расчет механизма следует начать с двухповодковой группы, состоящей из звеньев 2 и 3. Схема структурной группы, изображенная в масштабе со всеми приложенными силами, представлена на рис. Определению подлежать силы рефкции .

Задача нахождения сил и плеча 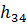является статически определимой задачей, поскольку для группы из двух звеньев можно составить 6 уравнений равновесия, и определению подлежат 6 неизвестных – величина и направления сил рефкций во вращательных кинемиатических парах А и В, величина и точка приложения силы 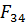в поступательной кинематической паре ползун – неподвижные направляющие ползуна.

Для удобства проведения расчета главный момент сил инерции можно заменить парой сил, приложенных в точках А и В звена 2. Значения сил будут

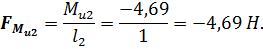
При графоаналисическом методе расчета следует неизвестную силу реакции 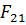представить в виде двух составляющих: нормальной 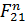, направленой вдоль звена, и касательной 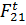, направленой перпендикулярно звену.

Все неизвестные силы реакции на рис.3.2,а направлены произвольно. Если из расчета какая-либо сила получится со знаком «минус», это значит, что ее дейстительное направление противоположно принятому.

Для системы сил, приложенных к звену 2, составим уравнение моментов относительно точки В

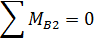
Если условиться, что моменты, направленные против часовой стрелки, считаются положительными, а по часовой стрелке – отрицательными, то уравнение моментов будет иметь вид

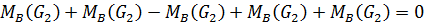
где неизвестная составляющая силы 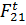направлена произвольно – вниз от точки А.

В развернутом виде уравнение перепишется как

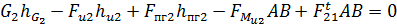
Откуда неизвестная сила 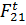будет

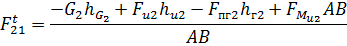
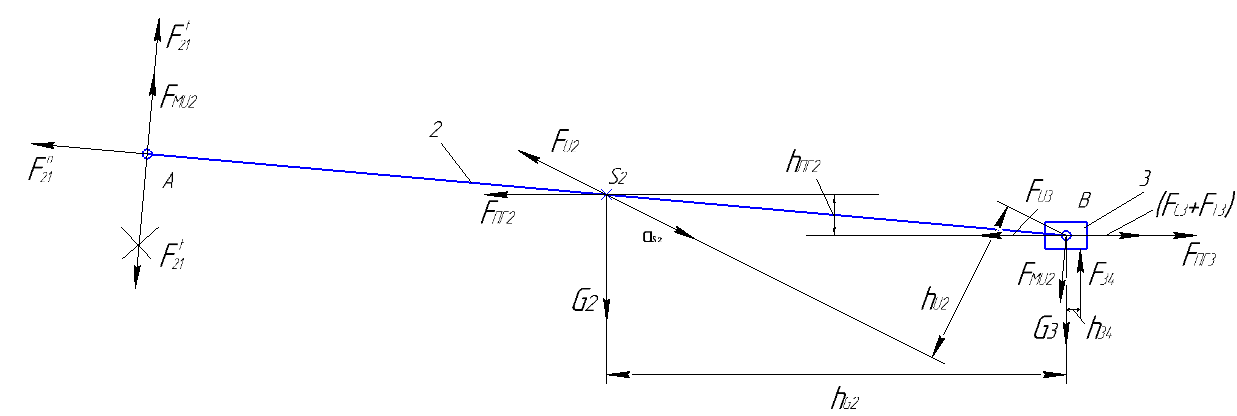
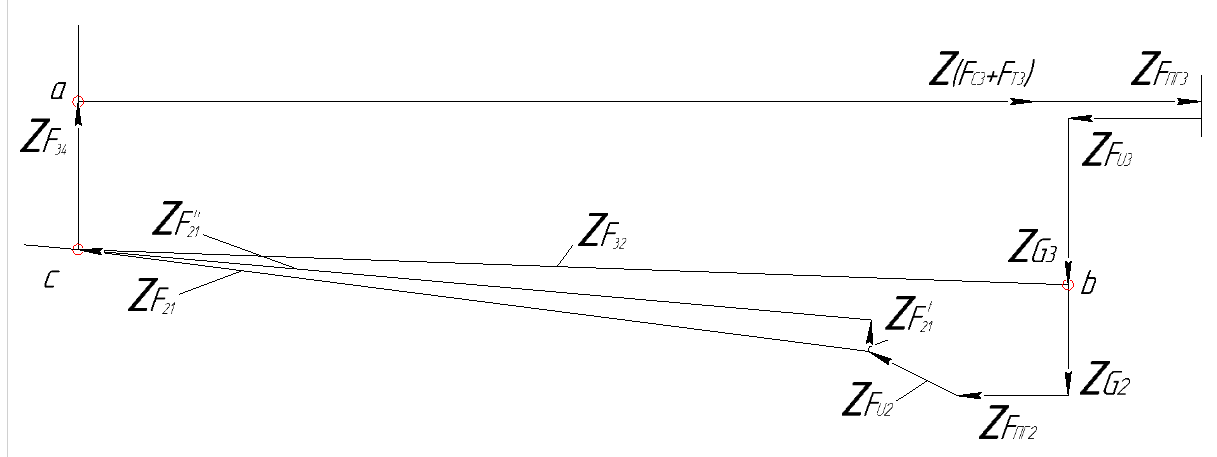
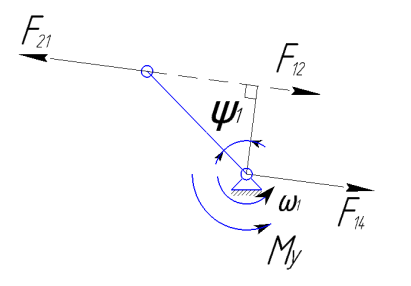
Рис.3.2. Схема к кинетостат. расчету двухповод. группы, ведущего звена и план сил 21

Здесь через h с индексами обозначены плечи соответствующих сил относительно точки В. Как видно из формулы для 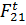, плечи сил могут быть взяты непосредственно из рисунка группы(рис.3.2,а), невзирая на масштаб его построения.

Следует отметить, что при определении численных значений сил рефкций как 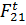, так и других, все силы следует брать по модулю, т.к. знак силы указывает на ее дейстительное направление, а на схеме механизма знак силы был учтен при изображении ее на рисунке.

Численное значение касательной составляющей 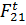для рассматриваемого примера будет

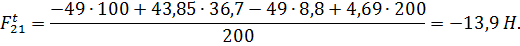
Знак «минус» означает, что сила 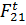должна быть направлена в проитвоположную от выбранного направления сторону, т.е. от точки А вверх, что показано на рис.

Для определения величин нормальной составляющей силы реакции в точке А 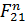и 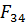составим векторное уравнение равновесия структурной группы, сгруппировав силы по звеньям:

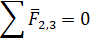
или

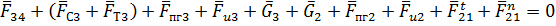
В уравнении силы, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению – одной чертой.

Решим векторное уравнение графически путем построения многоугльника сил(рис.3.2,б). Для этого необходимо выбрать масштабный коэффициент построения плана сил 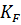, используя любую известную силу, лучше максимальную: у нас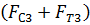

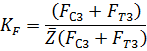
Если рассматриваемого примера отрезок 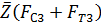, изображающий сумму сил 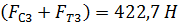, выбрать равным 200 мм, то масштабный коэффициент плана сил будет “удобным ” числом :

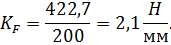
Тогда отрезок, изображающие остальные известные силы, будут

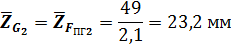
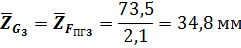
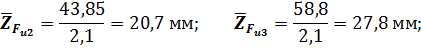
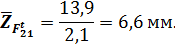
Построение силового многоугольника начнем с линии дейстивия силы 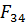, перпендикулярной оси x (рис.3.2,б),. Из призвольной точки a на этой линии, которая является точкой конца отрезка ,изображающего вектор силы 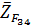, проведем вектор 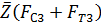, известный по величине и направлению. Из конца этого вектора проведем следующий известный вектор 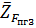и так далее согласно векторному уравнению сил. Из конца последнего известного вектора 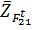проводим линию действия силы 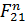, параллельную АВ. Пересечение в точке с этой линии и первой, перпендикулярной оси x, определяет искомые отрезк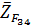и и 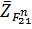. Измерив их длины, определим значения сил:

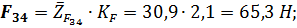
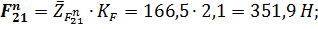
Полный вектор силы 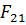равен геометрической сумме нормальной и касательной его составляющих

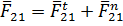
Величина вектора

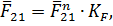
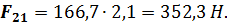
Для силы 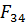необходимо определить точку ее приложения. Воспользуемся уравнением моментов для звена 3 относительно точки В

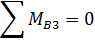
или

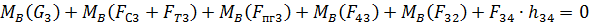
Так как для рассматриваемого примера все остальные силы проходят через точку В, то и сила 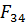также проходит через эту точку и ее плечо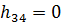

Для определеня усилия во вращательной кинематической паре В можно рассмотреть равновесие одного из звеньев - 2 или 3. Запишем условие равновесия сил, действующих на звено 3:

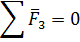
или

Неизвестный вектор силы 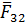определим с помощью построенного многоугольника сил на рис.3.2,б, соединив точки b и c :

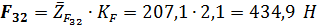
С помощью условия равновесия сил на звене 2 можно было определить усилие 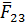, при этом очевидно, что

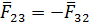
Рассмотрим равновесие ведущего звена 1 механизма рис.3.2,в. На это звено действует известная сила рефкций 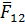во вращательной кинематической паре А:

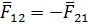
Требуется определить силу реакции 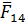в шарнире 0 и уравновешивающий момент .

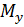Из уравнения моментов для звена 1 относительно точки 0 определим уравновешивающий момент: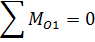

или

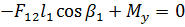
Здесь 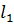- действительная длина ведущего звена; 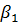- угол между звеном 1 и перпендикуляром, опущенным на направление силы 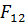(берётся из чертежа).

Направление неизвестного момента 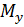взято произвольным (у нас против часовой стрелки). Из уравнения определяется величина уравновешивающего момента на рис. следует сменить на противоположное.

Момент 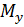, совпадающий по направлению с положительной угловой скоростью 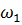будет отрицательным.

Для рассматриваемого примера

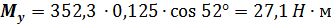
И является положительным

Уравнение равновесия ведущего звена имеет вид

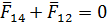
Отсюда

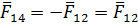
Таким образом