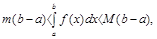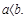ІІ. Властивості визначеного інтегралу.
Зміст теми.
І.До поняття визначеного інтегралу приводить задача з визначення площі криволінійної трапеції.
Фігуру, обмежену неперервною кривою 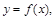 відрізком
відрізком 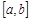 осі ОХ і прямими
осі ОХ і прямими 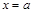 і
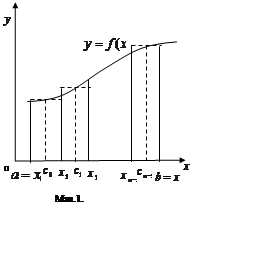
і 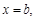 називають криволінійною трапецією (мал.1). Розіб’ємо відрізок
називають криволінійною трапецією (мал.1). Розіб’ємо відрізок 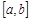 довільним чином на
довільним чином на 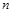 рівних частин. Точки поділу позначимо:
рівних частин. Точки поділу позначимо: 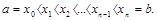 З цих точок проведемо перпендикуляри до перетину з кривою
З цих точок проведемо перпендикуляри до перетину з кривою 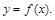
 Отримаємо
Отримаємо 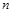 малих криволінійних трапецій, сума площ яких дає нам площу криволінійної трапеції. В центрі відрізків
малих криволінійних трапецій, сума площ яких дає нам площу криволінійної трапеції. В центрі відрізків 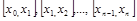 візьмемо точки
візьмемо точки 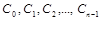 і проведемо перпендикуляри ( штрихові лінії ) від цих точок до перетину з кривою
і проведемо перпендикуляри ( штрихові лінії ) від цих точок до перетину з кривою 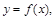 а потім побудуємо прямокутники, в основі яких лежать відрізки
а потім побудуємо прямокутники, в основі яких лежать відрізки 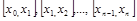 , а висоти, відповідно, ординати
, а висоти, відповідно, ординати 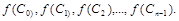 Утворилася ступінчата фігура, площа якої
Утворилася ступінчата фігура, площа якої 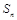 наближається до площі криволінійної трапеції
наближається до площі криволінійної трапеції 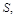 причому тим точніше, чим більше
причому тим точніше, чим більше 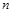 .
.
Знайдемо 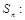
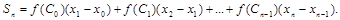
Всі доданки цієї суми відрізняються тільки індексами біля незалежної змінної, тому скорочено цю суму можна записати так:
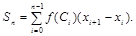 (1)
(1)
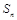 - це інтегральна сума. Символ
- це інтегральна сума. Символ 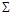 (грецька буква “сигма”) означає, що потрібно додати вирази, що в правій частині (1), надаючи індексу
(грецька буква “сигма”) означає, що потрібно додати вирази, що в правій частині (1), надаючи індексу 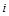 всі цілі значення, починаючи від значення , вказаного під символом “сигма”, до значення, вказаного над цим символом.
всі цілі значення, починаючи від значення , вказаного під символом “сигма”, до значення, вказаного над цим символом.
Якщо у виразі (1) збільшувати число 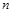 так, щоб довжина відрізка
так, щоб довжина відрізка 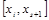 =
= 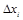 прямувала до нуля, то площа
прямувала до нуля, то площа 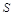 криволінійної трапеції буде дорівнювати границі інтегральної суми
криволінійної трапеції буде дорівнювати границі інтегральної суми 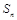 :
:
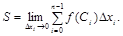 (2)
(2)
Границя інтегральної суми, при умові, що , називається визначеним інтегралом від функції на відрізку і позначається

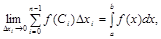 (3)
(3)
де 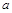 - нижня межа інтегрування,
- нижня межа інтегрування, 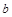 - верхня межа інтегрування,
- верхня межа інтегрування, 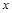 -змінна інтегрування.
-змінна інтегрування.
Не для всякої функції 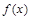 існує визначений інтеграл. Функція
існує визначений інтеграл. Функція 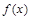 , для якої існує визначений інтеграл, називається інтегрованою на проміжку
, для якої існує визначений інтеграл, називається інтегрованою на проміжку 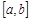 . Якщо
. Якщо
функція 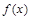 обмежена на проміжку
обмежена на проміжку 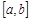 і неперервна на ньому, то вона інтегрована на цьому проміжку.
і неперервна на ньому, то вона інтегрована на цьому проміжку.
Якщо межі інтегрування є сталими величинами, то визначений інтеграл є стале число.
Зв’язок між визначеним і невизначеним інтегралом встановлює формула Ньютона – Лейбніца:
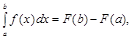 (4)
(4)
де 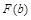 і
і 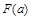 - значення первісної функції, взяті в точках верхньої і нижньої границі.
- значення первісної функції, взяті в точках верхньої і нижньої границі.
ІІ. Властивості визначеного інтегралу.
1. Визначений інтеграл не залежить від позначення змінної
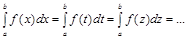 ,
,
оскільки результат інтегрування - число, яке не залежить від того, якою буквою позначено аргумент підінтегральної функції.
2. Визначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій, заданих на відрізку 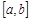 дорівнює алгебраїчній сумі визначених інтегралів:
дорівнює алгебраїчній сумі визначених інтегралів:
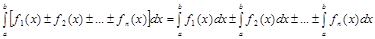 .
.
3. Сталий множник 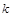 виноситься за знак визначеного інтегралу:
виноситься за знак визначеного інтегралу:
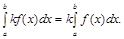
4. Якщо верхню і нижню межі інтегрування поміняти місцями, то визначений інтеграл змінить знак на протилежний при збереженні абсолютної величини
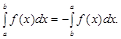
5. Якщо межі інтегрування рівні, 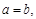 то визначений інтеграл дорівнює нулю:
то визначений інтеграл дорівнює нулю:
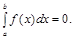
6. 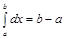 при
при 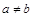 .
.
7. Адитивна властивість: якщо проміжок 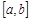 розбити на дві частини
розбити на дві частини 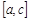 і
і 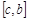 , то
, то
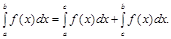
8. Якщо підінтегральна функція на проміжку інтегрування зберігає постійний знак, то інтеграл буде число того ж знаку, що і функція, тобто якщо 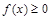 , то
, то
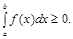
9. Якщо 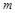 - найменше, а
- найменше, а 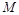 - найбільше значення функції
- найбільше значення функції 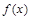 на проміжку
на проміжку 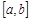
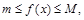
то значення визначеного інтегралу знаходяться між добутками найбільшого і найменшого значення підінтегральної функції на довжину інтервалу інтегрування, тобто