Статистические модели разрушения

Модели усталостного разрушения

Усталостные разрушения происходят при многократном повторении циклов нагружений и обычно связаны с динамическими напряжениями при различного рода колебаниях.

При действии напряжений

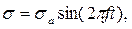(22)

где σ_а – амплитуда переменных напряжений;

f – частота колебаний в Гц, детерминированная модель усталостного разрушения может быть принята в виде:

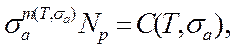(23)

где N_p – долговечность (число циклов до появления микротрещины).

Величина σ_а представляет собой ограниченный предел выносливости материала (при N_p). Эта зависимость (23) справедлива при многоцикловой усталости (N_p>10⁵ циклов).

Сопротивление усталости материалов по ГОСТу 23026-78 характеризуется пределом выносливости, соответствующим базовому числу циклов N_Б; обычно N_Б=10⁷ циклов.

Учет влияния асимметрии цикла нагружения осуществляется с помощью введения эквивалентного напряжения:

σ_э=σ_а+ψ_σσ_m , (24)

где σ_а – амплитуда переменных напряжений;

ψ_σ – коэффициент постоянных напряжений;

σ_m – статическое напряжение.

Обычно принимают:

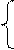ψ_σ = σ_-1/σ_дл , если σ_m >0;

0, если σ_m<0.

Модель усталостного разрушения для асимметричных циклов нагружения имеет вид:

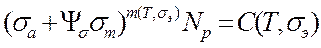(25)

При сложном напряженном состоянии под σ_а следует понимать интенсивность переменных напряжений и определять его по формуле:

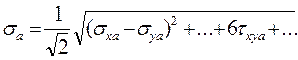(26),

где σ_xa , σ_ya , ..., τ_xya , ... – амплитуды компонентов переменного напряженного состояния.

Статистические модели разрушения

Экспериментальные исследования показывают, что параметры прочности, характеризующие сопротивление материалов разрушению (пределы прочности, текучести, выносливости и т.п.) имеют существенное рассеяние. Для оценки надежности конструкций необходимо знать вероятности минимальных значений параметров прочности.

В производстве нельзя собрать два полностью идентичных двигателя – они будут отличаться по своим параметрам работы (частотам вращения роторов, температуре газов в турбине и т.п.).

Параметры работы двигателя, в свою очередь, являются функциями температуры и давления атмосферного воздуха и зависят от условий эксплуатации. Нет двух полностью идентичных полетов одного и того же самолета по атмосферным условиям эксплуатации. Следовательно, нагруженность деталей авиационного двигателя является величиной случайной и обладает определенным рассеянием.

В связи с вышеизложенным использование статистических моделей разрушения является актуальным. Параметры прочности на нагруженности в этом случае рассматриваются как непрерывные случайные величины (или случайные процессы), характеризующиеся соответствующими статистическими распределениями.