Плоские статически неопределимые рамы
Для плоской статически неопределимой рамы из стального двутавра заданы расчётные нагрузки F, q и расчётное сопротивление материала R.
Требуется:
1) раскрыть статическую неопределённость;
2) построить эпюры внутренних сил М, Q, N;
3) из расчёта на прочность по предельным состояниям определить номер двутавра;
4) вычислить перемещение точки А и угол поворота сечения В.
Исходные данные
| Шифр | l м | h м | a м | F кН | q кН/м | R МПа |  |
| 31-6 | 2,1 | 2,6 | 0,9 |
 |
Решение
Степень статической неопределённости плоской рамы вычисляется по формуле
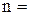 – (3Д–2Ш–С),
– (3Д–2Ш–С),
где Д =1 – число дисков, Ш = 0 – число шарниров соединяющих жёсткие элементы, С = 1 + 1 +3 = 5 – число опорных стержней (заделка эквивалентна трём опорным стержням!). Следовательно,
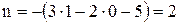 .
.
Система два раза статически неопределима.
Будем раскрывать статическую неопределённость с помощью метода сил. Независимо от конкретного выбора лишних неизвестных сил Х1, Х2 для их определения будет использована каноническая система уравнений
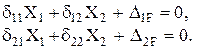 (1)
(1)
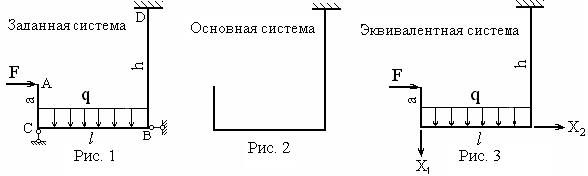
Отбрасываем две связи, наложенные на раму в виде шарнирно подвижных опор, и получаем из заданной системы (рис. 1) основную систему (рис. 2). Она должна быть, во-первых, геометрически неизменяемой жёсткой конструкцией, т. е. способной нести внешнюю нагрузку, и, во-вторых, уже статически определимой системой. Очевидно, что выбранная основная система обладает такими свойствами.
 |
Прикладываем к основной системе заданную нагрузку и неизвестные опорные реакции Х1, Х2 в отброшенных связях и получаем эквивалентную систему рис. 3. Система уравнений (1) является математическим выражением факта, что перемещения в направлениях неизвестных сил X1 и Х2 должны равняться нулю, поскольку в местах их приложений на самом деле имеются опоры, не позволяющие перемещаться соответствующим точкам.
Для решения уравнений необходимо сначала найти коэффициенты и свободные члены системы (1). Они представляют собой перемещения в направлениях сил X1 и Х2 от единичных сил 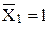 ,
, 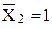 и нагрузки F. Отсюда следует, что необходимо построить эпюры изгибающих моментов от этих сил. Влияние продольных и поперечных сил на величину перемещений весьма незначительное, поэтому они не учитываются в вычислениях.
и нагрузки F. Отсюда следует, что необходимо построить эпюры изгибающих моментов от этих сил. Влияние продольных и поперечных сил на величину перемещений весьма незначительное, поэтому они не учитываются в вычислениях.
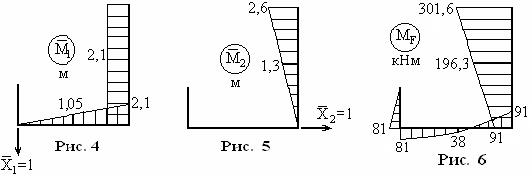
Эпюры изгибающих моментов построены по их значениям в отдельных характерных точках рамы. Они вычисляются с помощью метода сечений несложным путём и поэтому соответствующие выкладки здесь не приводятся. Результатом действий являются эпюры, представленные на рис. 4, 5, 6. При этом соблюдается правило построения эпюры изгибающих моментов, по которому ординаты откладываются со стороны растянутых волокон.
Теперь приступим к определению перемещений.
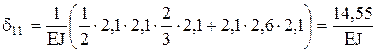 ,
,
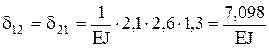 ,
, 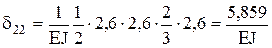 ,
,
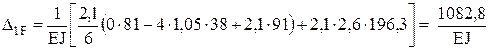 ,
,
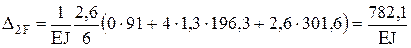 .
.
Подстановка в систему уравнений (1) и сокращение на EJ даёт
14,55X1 + 7,098X2 + 1082,8 = 0,
7,098X1 + 5,859X2 +782,1 = 0.
Решая эту систему уравнений, получим
X1 = -22,74 кН, X2 = -105,9 кН.
Полученные знаки минус в ответе показывают, что силы Х1, Х2 направлены противоположно изображённым на рис. 3.
Отметим на рис. 1 дополнительно точки C и D. Тогда получается, что рама имеет три участка AC, CB, BD. Построим для них эпюры продольных сил N, поперечных сил Q и изгибающих моментов M с помощью метода сечений.
Участок АС, 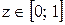 м
м
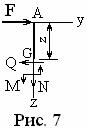 Проводим сечение произвольно внутри участка, выбираем для рассмотрения верхнюю отсечённую часть (рис. 7), показываем оси z и y, отмечаем переменное расстояние до сечения и точку G. Далее необходимо на схеме показать искомые внутренние силы, направления которых заранее неизвестны. Направления сил можно избирать произвольно и будут получены правильные ответы. Но при этом их знаки в конце вычислений придётся приводить в соответствие с правилами знаков сопротивления материалов. Чтобы избежать этих дополнительных процедур, целесообразно заранее намечать для внутренних сил положительные направления. В этом случае в ответах будут получены знаки, автоматически учитывающие установленные правила для внутренних сил.
Проводим сечение произвольно внутри участка, выбираем для рассмотрения верхнюю отсечённую часть (рис. 7), показываем оси z и y, отмечаем переменное расстояние до сечения и точку G. Далее необходимо на схеме показать искомые внутренние силы, направления которых заранее неизвестны. Направления сил можно избирать произвольно и будут получены правильные ответы. Но при этом их знаки в конце вычислений придётся приводить в соответствие с правилами знаков сопротивления материалов. Чтобы избежать этих дополнительных процедур, целесообразно заранее намечать для внутренних сил положительные направления. В этом случае в ответах будут получены знаки, автоматически учитывающие установленные правила для внутренних сил.
Будем придерживаться следующих правил. Продольные силы N положительны, если они растягивающие. Поперечные силы Q положительны, если они создают момент, направленный по часовой стрелке относительно отсечённой части. С учётом сказанного намечены направления стрелок на рис. 7. Изгибающие моменты не имеют правила знаков для вертикальных участков, поэтому соответствующее направление здесь избрано произвольно. В то же время для них существует упомянутое выше правило построения эпюры (со стороны растянутых волокон), и его необходимо соблюдать.
Далее составляем уравнения равновесия и по ним определяем внутренние силы.
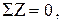
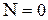 .
.
Результат нулевой, поэтому на этом участке (рис. 10) эпюра N не строится.
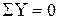 , F – Q = 0, Q = F = 81 кН.
, F – Q = 0, Q = F = 81 кН.
Поперечная сила здесь является постоянной величиной, и ей соответствует эпюра данного участка на рис. 11.
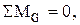 F z – M =0, M = F z = 81 z.
F z – M =0, M = F z = 81 z.
Как видим, изгибающие моменты являются линейной функцией. Для построения соответствующего графика необходимо иметь две точки. Найдём значения момента в концевых сечениях
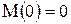 ,
, 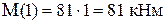 .
.
Для нижнего конца получен знак плюс, означающий, что направление момента, показанное на рис. 7, совпадает с действительным. Из этого следует, что левые волокна рамы в этом месте будут растянутыми. И именно с этой стороны откладывается полученное значение на эпюре (рис. 12).
Участок СВ, 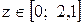 м
м
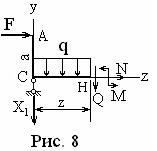 Руководствуясь аналогичными соображениями, рассмотрим левую отсечённую часть (рис. 8).
Руководствуясь аналогичными соображениями, рассмотрим левую отсечённую часть (рис. 8).
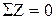 , F + N = 0, N = -F = - 81 кН.
, F + N = 0, N = -F = - 81 кН.
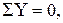
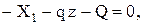
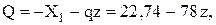
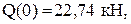
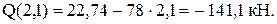
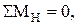 F a - X1 z -
F a - X1 z - 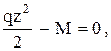
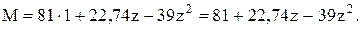
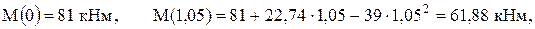
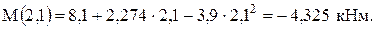
На этом участке знак поперечной силы изменяется с плюса на минус. Следовательно, имеется максимум функции М(z). В этом сечении поперечная сила должна равняться нулю, т. е.
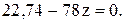
Отсюда находим соответствующее значение
z0 = 22,74/78 = 0,272 м
и максимальное значение изгибающего момента в сечениях участка CB
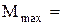
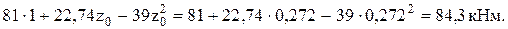
По этим результатам построены эпюры внутренних сил участка CB на рис. 10 – 12.
Участок BD, 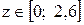 м.
м.
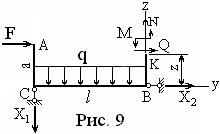 После того, как будет проведено произвольное сечение внутри этого участка, может показаться целесообразным рассматривать верхнюю отсечённую часть. Однако это не так. Причина здесь в том, что в верхней опоре в виде заделки действуют три неизвестные опорные реакции: две силы и момент. Без их предварительного определения, что будет связано с большим объёмом вычислений, уравнения равновесия невозможно составлять. Следовательно, и внутренние силы не могут быть найдены. Поэтому лучше рассматривать для этого участка нижнюю отсечённую часть, показанную на рис. 9. Тогда имеем
После того, как будет проведено произвольное сечение внутри этого участка, может показаться целесообразным рассматривать верхнюю отсечённую часть. Однако это не так. Причина здесь в том, что в верхней опоре в виде заделки действуют три неизвестные опорные реакции: две силы и момент. Без их предварительного определения, что будет связано с большим объёмом вычислений, уравнения равновесия невозможно составлять. Следовательно, и внутренние силы не могут быть найдены. Поэтому лучше рассматривать для этого участка нижнюю отсечённую часть, показанную на рис. 9. Тогда имеем
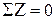 ,
, 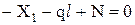 ,
,
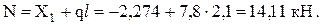
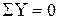 ,
, 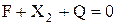 ,
, 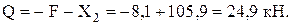
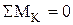 ,
, 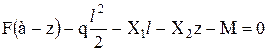 ,
,
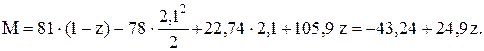
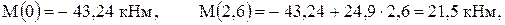
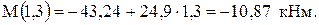
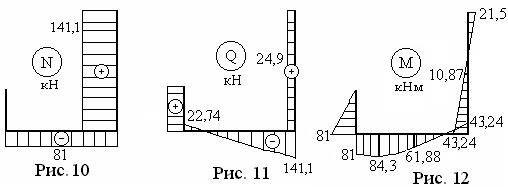 |
По этим результатам завершается построение эпюр, представленных на рис. 10 – 12.
Перейдём к определению необходимого двутаврового сечения балки. От продольной силы и изгибающего момента в поперечном сечении рамы возникают нормальные напряжения у, а от поперечной силы – касательные напряжения ф. Последние влияют на прочность таких рам весьма незначительно, поэтому поперечную силу не будем принимать во внимание.
Простой визуальный анализ эпюр N (рис. 10) и M (рис. 12) обнаруживает, что наибольшие нормальные напряжения, имеющие преобладающее влияние на прочность балки, возникают в сечении участка BD с самым большим изгибающим моментом (опасное сечение). Здесь
N = 81 кН, М = 84,3 кНм.
Условие прочности по методу предельных состояний имеет вид
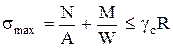 . (2)
. (2)
В неравенстве (2) содержатся две неизвестные характеристики сечения двутавра: площадь А и осевой момент сопротивления W. Поэтому прямое вычисление их значений невозможно. В первом приближении предположим, что нормальные напряжения от продольной силы малы и, игнорируя N, определим требуемый момент сопротивления
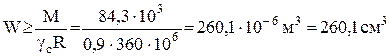 .
.
По таблице ГОСТ 8239-89 ближайшим двутавром с моментом сопротивления больше вычисленного является номер 24 с характеристиками:
A = 34,8 см2, W = 289 см3.
Подставляя в условие прочности (2), имеем
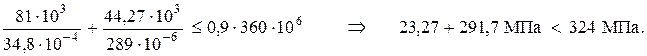
Окончательно имеем
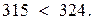
Очевидно, что прочность обеспечивается двутавром номер 24.
Одновременно подсчёты подтвердили предположение о малости нормальных напряжений от продольной силы по сравнению с напряжениями от изгибающего момента.
Перейдём к определению перемещений. Перемещения в точках А и В будем вычислять с помощью метода Мора по формуле
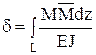 . (3)
. (3)
Здесь Е = 210 ГПа – модуль упругости стали, J = 3460 см4 – осевой момент поперечного сечения двутавра номер 24, взятый из сортамента прокатной стали, L – область интегрирования, включающая все участки рамы. Другие слагаемые формулы Мора не учитываются ввиду их малости по сравнению.
Интеграл в правой части (3) удобно вычислять с помощью способов Верещагина и Симпсона. Для этого строим единичные эпюры (рис. 13, 14). от единичных нагрузок, прилагаемых в точках А и В.
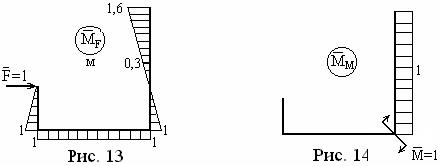
Перемножение этих эпюр с эпюрой М (рис. 12) дает горизонтальное перемещение точки А
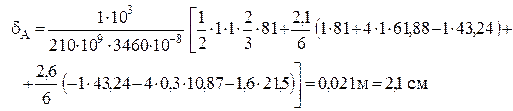
и угол поворота сечения, проходящего через точку В,

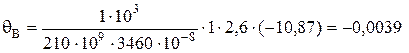 рад.
рад.
Из полученных знаков ответов следует, что линейное перемещение точки А по направлению совпадает с направлением единичной силы, показанным на рис. 13, т.е. будет происходить вправо. Сечение рамы в точке В поворачивается против хода часовой стрелке, т. е. против направления стрелки на рис. 14.
ВАРИАНТЫ ЗАДАНИЙ
| Второе число шифра | l м | h м | a м | F кН | q кН/м | M кНм | R МПа |  |
| 3,2 | 1,4 | 0,9 | ||||||
| 4,2 | 0,8 | |||||||
| 4,2 | 1,2 | 1,0 | ||||||
| 5,1 | 1,6 | 0,8 | ||||||
| 3,1 | 1,4 | 0,9 |
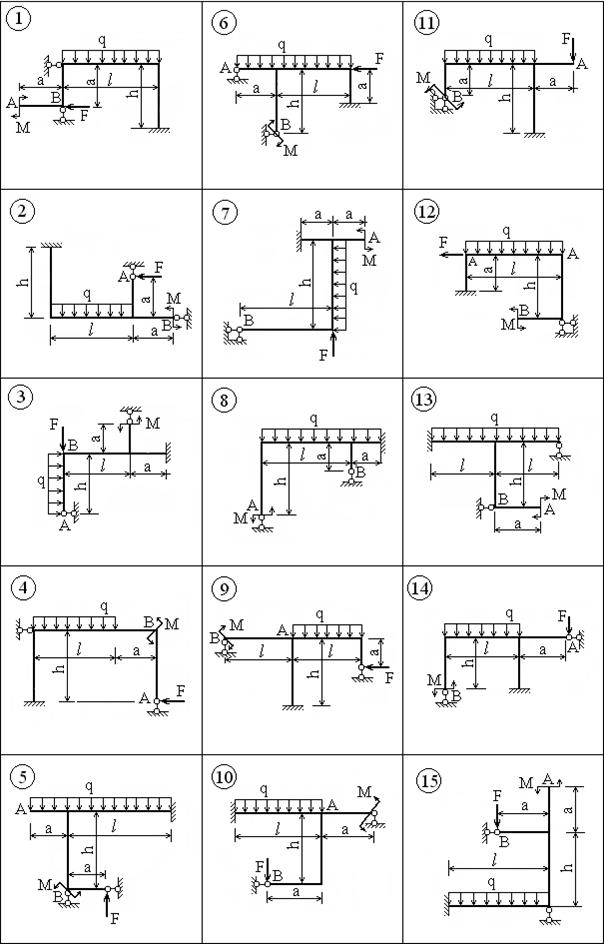
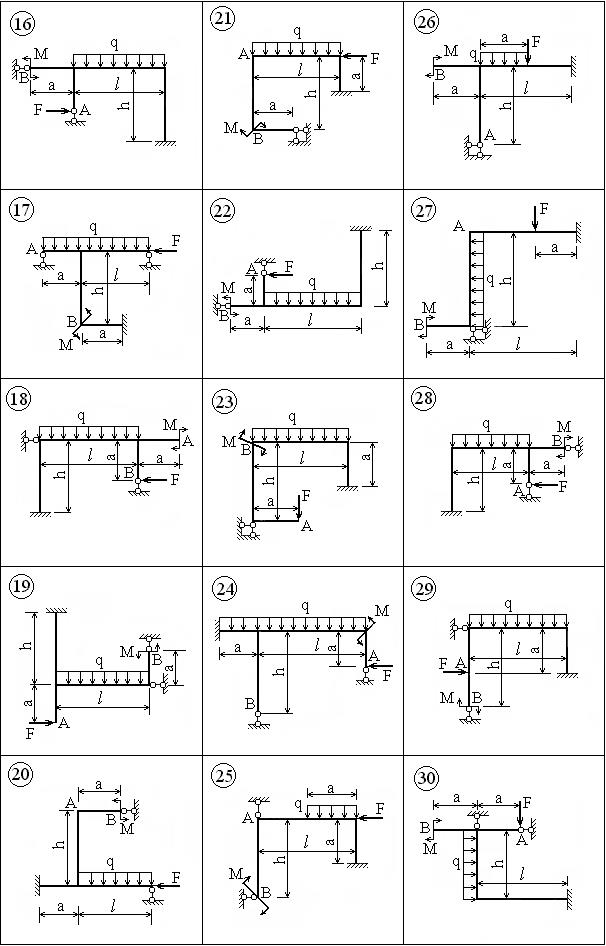
Задача 5
