Компоненты автомобильного бензина

Характеристика №1 №2 №3 №4

октановое число 68 72 80 90

содержание серы, % 0.35 0. 35 0.3 0.2

ресурсы, т 700 600 500 300

себестоимость, д.е./т 40 45 60 90

Требуется определить, сколько тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной. Составить экономико-математическую модель задачи. Построить экономико-математическую модель задачи.

Задача № 1.15.

Из трех продуктов – I, II, III составляется смесь. В состав смеси должно входить не менее 6 ед. химического вещества А, 8 ед. - вещества В и не менее 12 ед. вещества С. Структура химических ве­ществ приведена в следующей таблице:

Продукт	Содержание химического вещества в 1 ед. продукции	Стоимость 1 ед. продукции
А	В	С
I II III		1.5		2,5

Составьте наиболее дешевую смесь. Построить экономико-математическую модель задачи.

Задача № 1.16.

Имеются три специализированные мастерские по ремон­ту двигателей. Их производственные мощности равны соответственно 100, 700, 980 ремонтов в год. В пяти районах, обслуживаемых этими мастерскими, потребность в ремонте равна соответственно 90, 180, 150. 120, 80 двигателей в год. Затраты на перевозку одного двигателя из районов к мастерским следующие:

Районы	Мастерские
	4,5 2,1 7,5 5,3 4,1	3,7 4,3 7,1 1,2 6,7	8,3 2,4 4,2 6,2 3,1

Спланировать количество ремонтов каждой мастерской для каждого из районов, минимизирующее суммарные транспортные расходы. Построить экономико-математическую модель задачи.

Задача № 1.17.

Для полива различных участков сада, на которых растут сливы, яблони, груши, служат три колодца. Колодцы могут дать соответственно 180, 90 и 40 ведер воды. Участки сада требуют для полива соответственно 100, 120 и 90 ведер воды. Расстояния (в метрах) от колодцев до участков сада указаны в следующей таб­лице:

Колодцы	Участки
сливы	яблони	груши

Как лучше организовать полив? Построить экономико-математическую модель задачи.

Задача № 1.18.

Имеются два элеватора, в которых сосредоточено соответ­ственно 4200 и 1200 т зерна. Зерно необходимо перевезти трем хлебозаводам в количестве 1000, 2000 и 1600 т каждому. Расстояние от элеватора до хлебозаводов указано в следующей таблице:

Элеваторы	Хлебозаводы
I

Затраты на перевозку 1 т продукта на 1 км составляют 25 д.е. Спланировать перевозки зерна из условия минимизации транс­портных расходов. Построить экономико-математическую модель задачи.

Задача № 1.19

Звероферма выращивает черно-бурых лисиц и песцов. На звероферме имеется 10 000 клеток. В одной клетке могут быть либо две лисы, либо 1 песец. По плану на ферме должно быть не менее 3000 лис и 6000 песцов. В одни сутки необходимо выдавать каждой лисе корма - 4 ед., а каждому песцу - 5 е.д. Ферма еже­дневно может иметь не более 200 000 единиц корма. От реализации одной шкурки лисы ферма получает прибыль 10 д.е., а от реализа­ции одной шкурки песца - 5 д. е.

Какое количество лисиц и песцов нужно держать на ферме, чтобы получить наибольшую прибыль? Построить экономико-математическую модель задачи.

Задача № 1.20.

Цех выпускает три вида деталей - . Каждая деталь обрабатывается тремя станками. Организация производства в цехе характеризуется следующей таблицей:

Станок	Длительность обработки детали (мин.)	Фонд врем. (час)
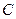I II II
Отпускная цена за одну деталь

Составить план загрузки станков, обеспечивающий цеху получение максимальной прибыли. Построить экономико-математическую модель задачи.