Практическое занятие 4 по теме «Дифференциальное исчисление функций многих переменных»
План:
1. Линии уровня, частные производные, градиент.
2. Дифференцируемость функции многих переменных.
3. Дифференциал функции многих переменных.
4. Плоскость и нормаль.
3. Оптимальные значения функции многих переменных.
5. Решение задач.
Контрольные вопросы и задачи
1. Дана функция z = f (x, y). Требуется: 1) найти частные производные 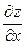 и
и 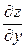 ;
;
2) найти полный дифференциал dz; 3) показать, что для данной функции справедливо равенство: 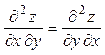 .
.
| Номер задания | Функция | Номер задания | Функция |
z = ln( 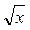 + 2y3) + 2y3) | z = (y2 – x) arcsin(2x) | ||
| z = tg(x – 5y2) | z = 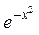 (y + 4x)2 (y + 4x)2 | ||
z = 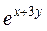 + cos(xy) + cos(xy) | z = ln3 (2y – x) | ||
| z = xcos(3x + 2y) | z = 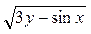 | ||
| z = x y + sin(x – y) | z = 4xy5– 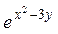 |
2. Дана сложная функция z= f (x, y, t), где 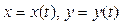 . Найти
. Найти 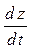 .
.
| Номер задания | Функция z= f (x, y, t) | Функции 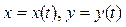 |
| u = (3t + 2x2 – y)3 | x = tgt, y = 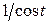 | |
u = (4t – x) 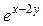 | x = 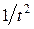 , y = , y = 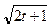 | |
| u = tsin(x3 + y) | x = 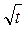 + 1, y = t4 + 1, y = t4 | |
u = tg(x + t ) 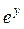 | x = ln(t3+ 1), y = t2 | |
u = 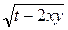 | x = sin3t, y = 1 – 5t | |
u= sin(x2 + y) – y 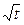 | x = 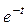 , y = , y = 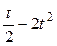 | |
u = 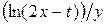 | x = cos4t, y = sin2t | |
| u = xctg(t – 3y) | x = 2 – 3t2, y = 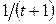 | |
| u = ln(2t + x – y2) | x = sin2t, y =3t – 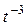 | |
| u = xy2+ cos(y + 2t) | x = 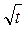 – t, y =2t – 4 – t, y =2t – 4 |
3. Поверхность σ задана уравнением z = f (x, y). Составить уравнения касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0, y0 – заданные числа.
| Номер задания | Уравнение поверхности | Значения x0, y0 |
| z = 3y – x2y + x | x0 = 1, y0 = 5 | |
z = 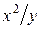 + 3x – y2 + 3x – y2 | x0 = 1, y0 = –1 | |
z = 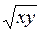 + x3 – 5 + x3 – 5 | x0 = 1, y0 = 4 | |
| z = y3x – y + x2 | x0 = –1, y0 = 2 | |
| z = cosy + 2x2 – xy | x0 = 2, y0 = 0 | |
| z = xy + y3 + 2x | x0 = 2, y0 = 1 | |
| z = ln(2x) – xy3 + y | x0 = 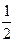 , y0 = 2 , y0 = 2 | |
z = 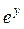 + x2y – x4 + 1 + x2y – x4 + 1 | x0 = –1, y0 = 0 | |
| z = ysinx + 3y2 | x0 = 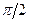 , y0 = –1 , y0 = –1 | |
z = 2y – 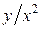 + x5 + x5 | x0 = 1, y0 = 3 |
4. Найти частные производные 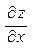 ,
, 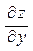 и
и 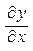 , если переменные x, y и z связаны равенством вида F(x, y, z) = 0.
, если переменные x, y и z связаны равенством вида F(x, y, z) = 0.
| Номер задания | Равенство F(x, y, z) = 0 | Номер задания | Равенство F(x, y, z) = 0 |
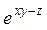 + 3x2siny – 2xz3 = 0 + 3x2siny – 2xz3 = 0 | sin(xy2) + z3xy2 + z4– x = 0 | ||
x 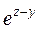 + zy + y2lnx – 2z = 0 + zy + y2lnx – 2z = 0 | (x – 2y)4 –5 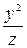 +3cosx – z5 = 0 +3cosx – z5 = 0 | ||
| ln(xz3) + y3 – 5x2yz4 + 5x = 0 | cos(y + ez) + xz5y + 3x3 + 4 = 0 | ||
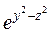 + ytgx – zx5 + 3y = 0 + ytgx – zx5 + 3y = 0 | (z – 2x)3 + 3y4 x – y2e2z –2x = 0 | ||
z 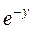 + + 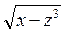 + y2zx – y5 = 0 + y2zx – y5 = 0 | sin2z +ln(x – y)+ 2x4 – 3yz2 = 0 |
5. Дана функция двух переменных: z = f (x, y) и уравнения границ замкнутой области D на плоскости xОy. Требуется: 1) найти наибольшее и наименьшее значения функции z в области D; 2) сделать чертёж области D в системе координат, указав на нём точки, в которых функция имеет наибольшее и наименьшее значения.
| Номер задания | Функция | Уравнения границ области D |
| z = x2 – xy + 2y2 + 3x + 2y +1 | x = 0, y = 0, x + y = –5 | |
| z = x2 + y2 – 6x + 4y + 2 | x = 1, y = –3, x + y = 2 | |
| z = 5x2 – 3xy + y2 + 5x + 4 | x = –1, y = –2, x + y = 1 | |
| z = x2 – 2y2+ 4xy – 6x – 1 | x = –1, y = 0, x + y = 3 | |
| z = x2 – 3xy + 4x + 8y | x = 0, y =4, x + y = –2 | |
| z = x2 – 4xy + 3y2 + x – y | x = –1, y = –1, y + x = 5 | |
| z = 10 – x – 2xy – x2 | x = – 3, y = – 1, x + y = 0 | |
| z = 2x2 + y2 – xy + x – y + 3 | x = –1, y = 2, x – y = 0 | |
| z = x2– y2 + xy – 3x + 1 | x = 0, y = 0, x + y = 4 | |
| z = x2 + y2 – xy + x – 4y | x = 1, y = 3, x + y = –3 |
6. Дано плоское скалярное поле U = U(x,y), точка M0(x0, y0) и вектор 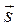 . Требуется: 1) найти уравнения линий уровня поля U; 2) найти градиент поля в точке M0 и производную
. Требуется: 1) найти уравнения линий уровня поля U; 2) найти градиент поля в точке M0 и производную 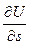 функции U(x,y) в точке M0по направлению вектора
функции U(x,y) в точке M0по направлению вектора 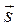 ; 3) построить в системе координат xОy 4-5 линий уровня, в том числе линию, проходящую через точку M0 и изобразить вектор
; 3) построить в системе координат xОy 4-5 линий уровня, в том числе линию, проходящую через точку M0 и изобразить вектор 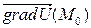 .
.
| Номер задания | Скалярное поле | Точка M0 (x0, y0) | Вектор 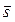 |
| U = x2 + 3y2 | M0(1, 1) | 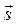 = 3 = 3 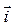 – 4 – 4 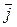 | |
| U = x2 – 2 y2 | M0(2, 1) | 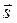 = 6 = 6 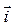 + 8 + 8 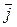 | |
| U = –3y– x2 | M0(–1, –1) | 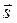 = = 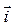 + 2 + 2 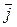 | |
| U = y2 – 4x | M0(–2, 1) | 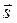 = –2 = –2 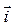 + 2 + 2 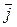 | |
| U = 2x2 – y2 | M0(1, 1) | 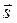 = – = – 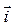 – 3 – 3 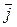 | |
| U = 2 x2 + y2 | M0(1, 2) | 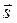 = 2 = 2 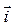 + 2 + 2 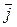 | |
| U = x3 – y | M0(1, –2) | 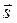 = –2 = –2 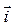 + + 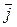 | |
| U =2x + y2 | M0(–2, 1) | 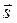 = = 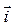 + + 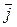 | |
| U = (x + 1)2 + y2 | M0(0, 2) | 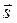 = = 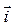 – 2 – 2 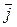 | |
| U = 3x2 – y2 | M0(1, –1) | 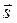 = –2 = –2 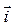 + 3 + 3 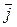 |
Литература
Основная:
1. Баврин И.И. Математика для гуманитариев: учебник для студентов учреждений высш. Проф. образования гуманитарных направлений. М.: Изд. центр «Академия», 2011. С. 143–155.
2. Высшая математика для экономистов / Под ред. Н.Ш. Кремера. М.: ЮНИТИ, 2002. С. 397–437.
3. Ильин В.А., Куркина А.В. Высшая математика: учеб. М.: Проспект, 2009. С. 366–420.
4. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М, 1997. С. 118–138.
5. Красс М.С. Математика для экономических специальностей: Учебник. М.: ИНФРА-М, 1999. С. 259–279.
Дополнительная:
1. Ганичева А.В. Краткий курс математического анализа: Учебное пособие. Тверь, 2002. С. 84–101.
2. Данчул А.Н., Митини А.И., Сафонова Т.Е., Симонов В.А. Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика. Учебно-методическое пособие / Под ред. А.Н.Данчула. М., 2004. С.28–39.
3. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. М.: МГУ им. М.В.Ломоносова, Издательство «ДИС», 1998. С. 101–119.
4. Кремер Н.Ш. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. Пособие. М.: Издательство Юрайт; ИД Юрайт, 2011. С.183–195.
5. Сборник задач по высшей математике для экономистов: Учебное пособие/ Под ред. В.И. Ермакова. М.: ИНФРА-М, 2004. С. 179–201.
