Раздел 3. Элементы линейной алгебры.
Тема 3.1. Матрицы. Определители матриц.
Матрица- это прямоугольная таблица чисел или других величин.
Например: На складах фирмы:
Склад 1 Склад 2 Склад 3
Сахар 200 100 150
Соль 350 200 180
Мука 400 250 260
Эти данные можно записать в форме матрицы (массива) чисел:
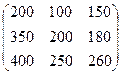
Коэффициенты при неизвестных, системы линейных уравнений.
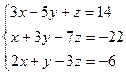
Так же могут быть выделены в отдельную матрицу коэффициентов:
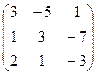
Любое число такого массива называется элементом матрицы.
Ряд чисел, расположенных в матрице горизонтально, называется строкой матрицы, а вертикально – столбцом.
Количество строк обозначается m, количество столбцов – n. Говорят матрица m x n.
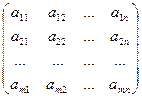
Если m=n, то матрица квадратичная. Элементы a11, a22,…amn образуют главную диагональ, от am1 до a1n – побочную диагональ.
Матрица называется треугольной, если все элементы расположенные ваше либо ниже главной диагонали равные нулю. Например:

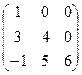
Операции над матрицами
Суммой (разностью) двух матриц А и В, имеющих m строк и n столбцов, называется матрица, полученная в результате сложения (вычитания) одноименных элементов матриц А и В.
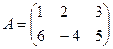 ;
; 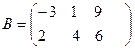
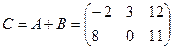
Произведением матрицы А на число k называется матрица, каждый элемент которой получен умножением соответствующего элемента данной матрицы А на число k.
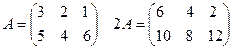
Умножение матрицы на матрицу.
Пусть i=1,2,3,…m – номер строки
J= 1,2,3…n – номер столбца
Тогда aij – общий элемент матрицы А
Произведением матрицы А на матрицу В называется матрица С, каждый элемент которой Сij равен сумме произведений элементов i-ый строки первой матрицы А на соответствующие элементы j-ого столбца второй матрицы В.
Например: 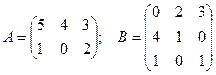
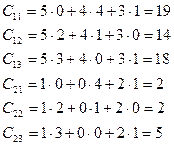
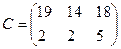
Определитель матрицы – это число, получаемое из элементов этой матрицы по определенному правилу. Обозначается det(A).
Определителем матрицы второго порядка (m=n=2) называется разность произведений элементов главной и побочной диагоналей.
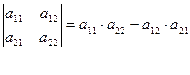
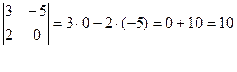
Определитель матрицы третьего порядка вычисляется по правилу треугольника.
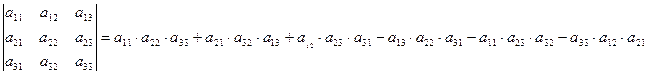
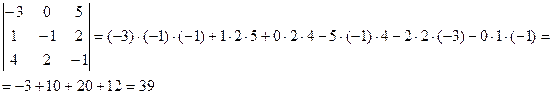
Основные свойства определителей.
1) Если одна из строк или один столбец определителя состоит из нулей, то определитель равен нулю.
2) Определитель, содержащий две одинаковые или пропорциональные строки (столбца), равен нулю.
3) От перестановки двух строк или столбцов определитель меняет только знак.
4) 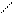 Если все элементы некоторой строки или столбца определителя умножить на число k=0, то сам определитель умножиться на это число.
Если все элементы некоторой строки или столбца определителя умножить на число k=0, то сам определитель умножиться на это число.
Тема 3.2. Системы линейных уравнений.
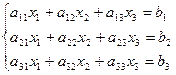 - система трех линейных уравнений с тремя
- система трех линейных уравнений с тремя
неизвестными
Метод Крамеразаключается в применении формулы Крамера:
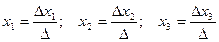
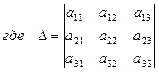
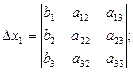
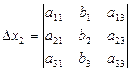 ;
; 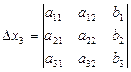
1) Если 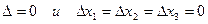 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
2) Если 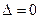 и хотя бы один
и хотя бы один 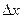 не равен 0, то система не имеет решений.
не равен 0, то система не имеет решений.
Метод Гаусса(метод последовательного исключения неизвестных). Систему уравнений приводят к эквивалентной системе с треугольной матрицей. Для этого используют следующие преобразования:
- Умножение и деление коэффициентов и свободного члена на число.
- Сложение и умножение уравнений.
- Перестановка уравнений.
Затем из треугольной матрицы находят неизвестные с помощью последовательных подстановок.
Пример:
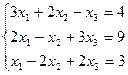

Составим расширенную матрицу:
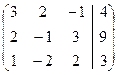
Поменяем для удобства строки местами
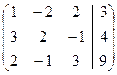 ~
~
Первую строку умножим на 3, и из полученной вычтем вторую, результат запишем во вторую строку, а первую затем разделим на 3
~ 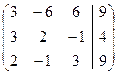 ~
~ 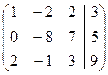 ~
~
Первую умножим на 2, и из полученной вычтем 3, результат запишем в третью строку, а первую затем разделим на 2
~ 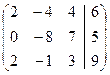 ~
~ 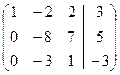 ~
~
Вторую строку умножим на 3, третью на 8. Из второй вычтем третью
~ 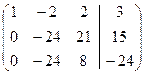 ~
~ 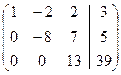
Получили треугольную матрицу.
Подставим неизвестные
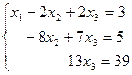 решим
решим 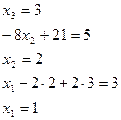 Ответ: х1=1; х2=2; х3=3
Ответ: х1=1; х2=2; х3=3
Раздел 4. Основы линейного программирования
Задача использования сырья.
Для изготовления n видов продукции Р используется m вида сырья: S
Запросы сырья, количество единиц сырья, затрачиваемого на изготовление единицы продукции, а так же величина прибыли, получаемой от реализации единицы продукции, приведены в таблице: Необходимо составить план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
| Вид сырья | Запасы сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |||
| P1 | P2 | … | Pn | ||
| S1 | в1 | a11 | а12 | … | a1n |
| S2 | в2 | a21 | a22 | … | a2n |
| … | … | … | … | … | … |
| Sm | вm | am1 | am2 | … | amn |
| Прибыль от единицы продукции | С1 | С2 | … | Сn |
Решение
Пусть х1 единиц продукции Р1 которое необходимо произвести
х2- пр. Р2 и т.п. хn дляРn
Тогда
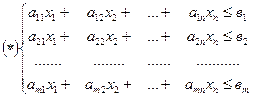
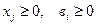
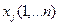
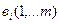
С1х1 – прибыль от реализации пр. Р1
Сnхn – прибыль от реализации пр. Рn
Общая прибыль 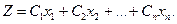
Задача состоит в том, чтобы найти наибольшее значение функции Z при ограничениях заданных системой
Замечания: Если в задачи требовалось использовать все сырьё, то составляется ситема уравнений.
Задача составления рациона
При откормки каждое животное ежедневно должно получать не менее в ед.питания вещества S.
Пусть m видов питания вещества S в количестве не менее вi(i=1,…,m) и используется n видов кормов
| Питательные вещества | Ко-во необходимых единиц питат. в-в | Количество единиц питательных веществ в 1 ед.(кг) корма | |||
| К1 | К2 | … | Кn | ||
| S1 | в1 | a11 | а12 | … | a1n |
| S2 | в2 | a21 | a22 | … | a2n |
| … | … | … | … | … | … |
| Sm | вm | am1 | am2 | … | amn |
| Стоимость 1 ед. корма | С1 | С2 | … | Сn |
Необходимо составить рацион нужной питательности, причем затраты на него должны быть минимальны.
Пусть х1, х2…хn количества корма К1, К2…Кn в дневном рационе
Тогда
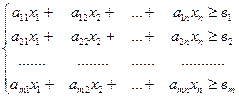
С1х1 – стоимость К1, если х1 единиц
Сnхn – стоимость Кn, если хn единиц
Общая стоимость 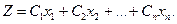
Цель найти минимальное значение Z при ограничениях указанных в системе.
Замечания: Если в задачи требовалось, что бы кол-во питательного вещества в корме было точным, то составляется система уравнений.
Общая задача линейного программирования состоит в изучении способов отыскания наибольшего или наименьшего значений линейной функции Z , при этом
Z- целевая функция , а совокупность значений х1, х2…хn , определяет оптимальный план.
Всякая другая совокупность х1, х2…хn удовлетворяющая системе неравенств определяет допустимый план.
Графический метод решения задачи линейного программирования
Пример 1.Задача на использование сырья . Данные в таблице.
| Вид сырья | Запасы сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |
| P1 | P2 | ||
| S1 | 20 | ||
| S2 | 40 | ||
| S3 | |||
| Прибыль от единицы продукции (руб) |
Необходимо составить оптимальный план выпуска продукции, чтобы при ее реализации получить максимальную проибыль, т.е. Z max.
Пусть х1, х2- количество единиц продукции Р1, Р2, которую нужно выпустить

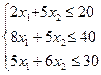 Z=50x1+40x2 (руб)
Z=50x1+40x2 (руб)
Найти х1, х2, чтобы Z max
Строим графики уравнений
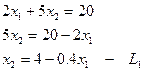
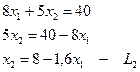





|

|


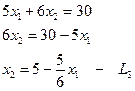
| Х1 | ||
| Х2 |

 L1:
L1:



 | |
 |
| Х1 | ||
| Х2 |
 L2:
L2:

 |
| Х1 | ||
| Х2 |
 L3:
L3:
ОАВСD – многоугольник допустимых решений Z = 50х1+40х2
Если Z=0, то 50х1+40х2=0
Х2= 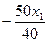
| Х1 | ||
| Х2 | -5 |
Х2= 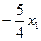
Вектор ON 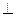 семейству параллельных прямых 50х1+40х2=Z его координаты (50;40) или 10(5;4).
семейству параллельных прямых 50х1+40х2=Z его координаты (50;40) или 10(5;4).
Прямую 50х1+40х2=0 перемещаем параллельно самой себе в направлении вектора ОN и видим, что наибольшее значение целевой функции достигает в точки С которая лежит на пересечении L2, L3, найдем эти координаты.
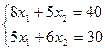
Метод Крамера:
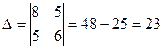
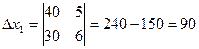
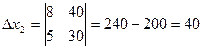
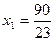
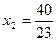
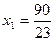
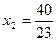
х1 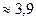 х2
х2 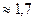
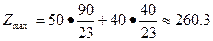
Таким образом, чтобы получить max прибыль надо выполнить х1 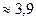 прод Р1
прод Р1
х2 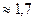 прод Р2
прод Р2
Пример 2. Задача на составление рациона.
| Питательные вещества | Количество необходимых питательных веществ | Количество единиц питательных веществ в 1 кг корма | |
| К1 | К2 | ||
| S1 | 9 | ||
| S2 | 8 | ||
| S3 | |||
| Стоимость 1 кг корма |
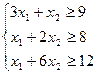 х1, х2 количества корма К1, К2 чтобы Zmin=4х1+6х2
х1, х2 количества корма К1, К2 чтобы Zmin=4х1+6х2
Строим графики уравнений
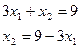
| Х1 | ||
| Х2 |
L1
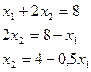
| Х1 | ||
| Х2 |
L2
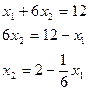
| Х1 | ||
| Х2 |
L3
ABC – неограниченный многоугольник - допустимое решение
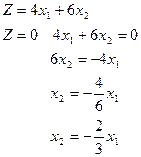
| Х1 | ||
| Х2 | -2 |
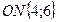
Вектор ОN перпендикулярен семейству параллельных прямых 4x1+6x2=Z. Прямую Z перемещаем параллельно самой себе в направлении вектора JN и видим, что наименьшее значение достигается в точке В.
Точка В – решение, и образуется при пересечении L1 и L2.
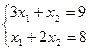
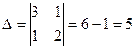
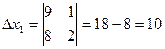
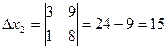
Х1=2 Х2=3
Т.е.если 2кг. – К1; 3кг. – К2, то затраты минимальные.
