Признак совместности системы линейных уравнений

Рассмотрим систему 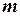уравнений с 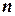неизвестными:

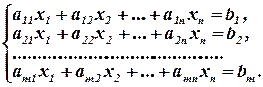
Матрица коэффициентов 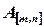и расширенная матрица 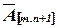имеют вид:

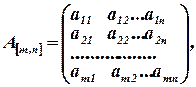
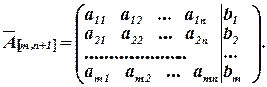
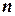Теорема Кронекера – Капелли. Система линейных уравнений с неизвестными совместна тогда и только тогда, когда ранг матрицы 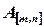равен рангу расширенной матрицы 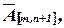т.е.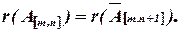

Из теоремы следует:

1) если 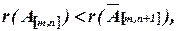то соответствующая система линейных уравнений несовместна;

2) если 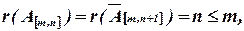то соответствующая система линейных уравнений определенная;

3) есл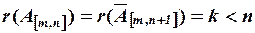и и 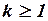, то соответствующая система линейных уравнений неопределенная.

Перечисленные следствия учитывают все многообразие систем линейных уравнений. Выполнение услови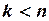й и 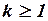соответствует выполнению также услови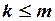й и 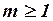. Например, пусть 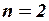и 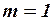, тогда в неопределенной системе линейных уравнений 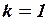,а для 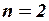и 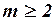в неопределенной системе линейных уравнений тоже .

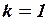Нахождение решений неопределенной системы линейных уравнений

Считая, что в совместной системе линейных уравнений все 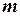уравнений независимы, ранг 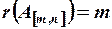и число уравнений меньше числа переменных 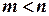, любые 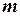переменных назовем базисными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные 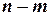переменных называются свободными.

Базисными могут быть разные группы из 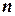переменных. Максимально возможное число групп базисных переменных равно числу способов выбора 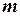переменных из их общего числа 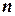, т.е. числу сочетаний .

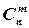Алгоритм решения неопределенной системы линейных уравнений, для которо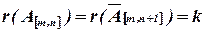й

и :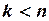

1) отбрасываются 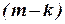уравнений, коэффициенты которых не вошли в определитель 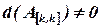максимального порядка;

2) в правую часть уравнений переносятся 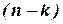свободных неизвестных, коэффициенты при которых не вошли в определитель 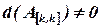максимального порядка;

3) решается система 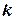уравнений с 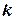базисными переменными, находящимися в левой части уравнений, и в результате 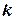базисных переменных выражаются через 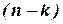свободных переменных.

▼

Пример

Решить методом Жордана-Гаусса систему линейных уравнений:

.

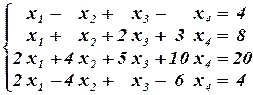Решение.

Расширенная матрица имеет вид:

.

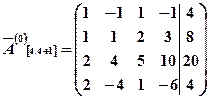Применяя элементарные преобразования (из второй строки вычитаем первую, из третьей и четвертой строк вычитаем две первые), получим:

.

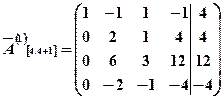В полученной матрице вторая, третья и четвертая строки линейно зависимы. Поэтому продолжая элементарные преобразования (из третьей строки вычитаем три вторых строки, к четвертой строке прибавляем вторую, а из первой строки вычитаем вторую), получим:

.

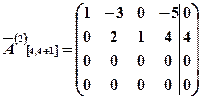Тогда исходная система эквивалентна следующей системе уравнений:

.

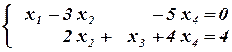Общее решение имеет вид:

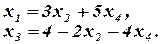
Найдем базисные решения. Для этого полагаем 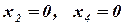, тогда 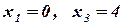. Базисное решение имеет вид: .

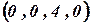Получим другое базисное решение. Для этого в качестве свободных неизвестных примем 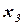и 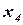. Выразим неизвестные 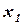и 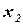через неизвестные 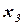и :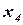

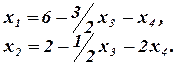
Тогда базисное решение имеет вид: .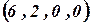

▲