Розподіл молекул за абсолютними значеннями швидкостей

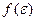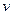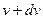Величина не залежить від напрямку швидкості, тому давайте краще перейдемо до розподілу за абсолютними значеннями. Позначимо ймовірність знайти швидкість за абсолютним значенням між та як 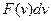. 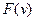в досить простий спосіб пов’язана із .

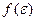Введемо поняття простору швидкостей. Якщо відкласти вздовж осей 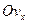, , 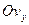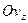прямокутної системи координат проекції швидкості 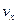, , 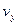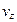будь-якої молекули газу, то можна побудувати простір швидкостей, кожна точка в якому буде відповідати визначеному наборові проекцій швидкості молекули газу (рис. 2).

На рис. 2 оберемо точку з координатами 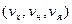і до цієї точки проведемо радіус-вектор 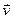. 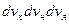- елементарний об’єм у просторі швидкостей, обраний поблизу заданої швидкості 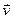. ( Скільки точок в ньому? - .)

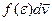Точки, що визначають швидкості, величина яких лежить в інтервалі 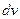поблизу обраного значення 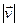, знаходяться в області між сферами радіусів 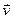та 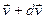. Проінтегрувавш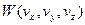и (при 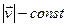) по всім можливим напрямкам 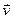у просторі швидкостей, отримаємо відносне число молекул 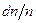, швидкості яких лежать в одиничному інтервалі 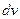поблизу даної швидкості 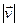(тобто розподіл за абсолютними значеннями швидкостей молекул). Ми інтегрувати не будемо. Це шар із середнім радіусом 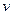і товщиною 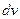. Отже його об’єм 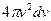. Об’ємна густина в цьому шарі постійна, оскільки залежить тільки від 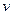. Тому шукана ймовірність 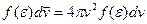. Порівнюємо із 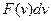і маємо

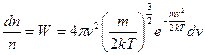. (3)

Формула (3) являє собою закон Максвела розподілу молекул за абсолютними значеннями швидкостей.Нагадаємо ще раз, що величина 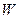дає нам ймовірність того, що величина швидкості будь-якої молекули газу має значення в інтервалі від 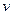до .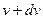

* Спробуйте дома отримати з функцію розподілу за значеннями кінетичної енергії.

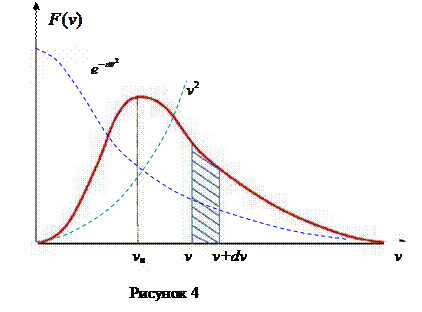Крива на рис. 4 є графіком функції 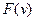. При збільшенні швидкості 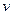множник вигляду 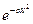спадає швидше ніж зростає множник 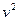. Функція починається в нулі (через те, що 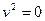), досягає максимального значення, а потім прямує до нуля.

При цьому, 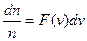- частина молекул, швидкості яких лежать у інтервалі від 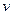до 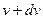, числено дорівнює площі заштрихованої смуги з основою 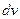і висотою .

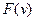Для того, щоб визначити ймовірність виявити швидкість молекул в інтервалі 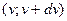необхідно обчислити інтеграл

.

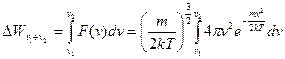Функція розподілу Максвела 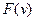, як видно з рис. 4, обертається в нуль при 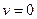і 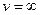. Це цілком зрозуміло, оскільки у газі немає ані нерухомих молекул, ані тих, що мають нескінчено великі швидкості. Нарешті, функція 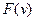має максимум при деякому значенні швидкості 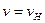. Це значення називають найбільш ймовірним. Ймовірність виявити у молекули швидкість 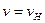- найбільша тому, що найбільша частина молекул має швидкості в інтервалі 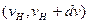поблизу .

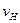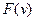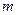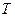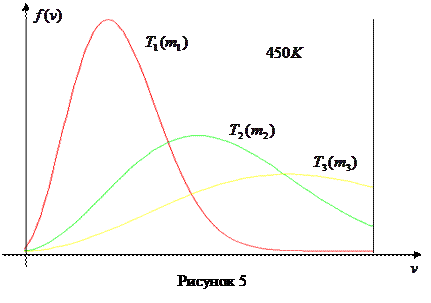
Вигляд кривої залежить від природи газу (оскільки формула (3) включає в себе - масу молекули) та вд абсолютної температури . Звичайно, з підвищенням 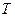(або зменшенням маси молекули) частина молекул, які мають більш високі швидкості збільшуються. В результаті вся крива зміщується разом із своїм максимумом у бік більших швидкостей, при цьому найбільш ймовірну швидкість має менша кількість молекул (максимум стає меншим). Площа, обмежена новою кривою і віссю 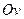, не змінюється і залишається рівною одиниці. На рис. 5 представлені криві, які можна розглядати або як криві розподілу для різних температур (при однаковій масі), або криві розподілу для різних мас молекул (при однаковій температурі).