Оверхности DirectDraw - вид доступа к видеопамяти

еркальное отражение

Отраженный луч падает в точку P в направлении i и отражается в направлении, задаваемом вектором r, определяемым следующим законом: вектор r лежит в той же плоскости, что и вектор i и единичный вектор внешней нормали к поверхности n, а угол падения 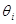равен углу отражения 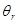(рис. 2).

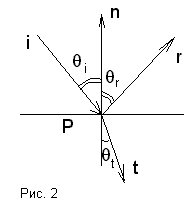Будем считать все векторы единичными. Тогда из первого условия следует, что вектор r равен линейной комбинации векторов i и n, то есть

r=αi+βn. (1)

Так же = ,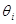

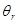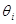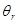то (-i, n) = cos = cos = (r, n).

Отсюда легко получается

r = i - 2(i, n)n. (2)

Несложно убедиться, что вектор, задаваемый соотношением (2), является единичным.

иффузное отражение

Идеальное диффузное отражение описывается законом Ламберта, согласно которому падающий свет рассеивается во все стороны с одинаковой интенсивностью. Таким образом не существует однозначно определенного направления, в котором бы отражался падающий луч, все направления равноправны и освещенность точки пропорциональна только доле площади, видимой от источника, то есть (i, n).

деальное преломление

Луч, падающий в точку P в направлении вектора i, преломляется внутрь второй среды в направлении вектора t (рис. 2). Преломление подчиняется закону Снеллиуса, согласно которому векторы i, n и t лежат в одной плоскости и для углов справедлива соотношение 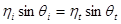. (3)

Найдем для вектора t явное выражение. Этот вектор можно представить в следующем виде:

r=αi+βn. (4)

Соотношение (3) можно переписать так:

,

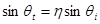где 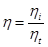. (5)

Тогда

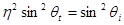
или

. (6)

Так как

,

то

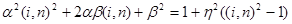. (7)

Из условия нормировки вектора t имеем

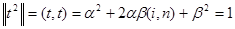. (8)

Вычитая это соотношение из равенства (7), имеем:

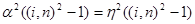, (9)

откуда .

Из физических соображений следует, что .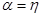

Второй параметр определяется из уравнения

, (10)

дискриминант которого равен

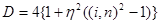. (11)

Решение этого уравнения задается формулой

(12)

и, значит, вектор

(13)

где 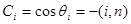. (14)

При этом случай, когда выражение над корнем отрицательно ( ) соответствует так называемому полному внутреннему отражению, когда вся световая энергия отражается от границы раздела сред и преломления фактически не происходит.

иффузное преломление

Диффузное преломление полностью аналогично диффузному отражению, при этом преломленный луч идет по всем направлениям t : (t, n) < 0 с одинаковой интенсивностью.

Рассмотрим теперь распределение энергии при отражении и преломлении. Из курса физики известно, что доля отраженной энергии задается коэффициентами Френеля

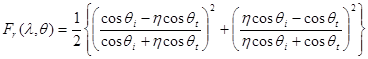. (15)

Существует другая форма записи этих соотношений:

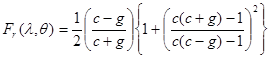, (16)

где 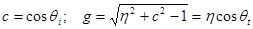. (17)

Формула (15) верна для диэлектрических материалов.

Для проводников обычно используется следующая формула

, (18)

где 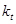— индекс поглощения.

Ясно, что все рассмотренные примеры являются идеализациями. На самом деле нет ни идеальных зеркал, ни идеально гладких поверхностей.

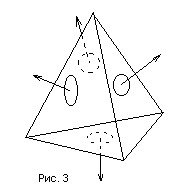
На практике обычно считают, что поверхность состоит из множества случайно ориентированных плоских идеальных микрозеркал (микрограней), с заданным законом распределения (рис. 3).

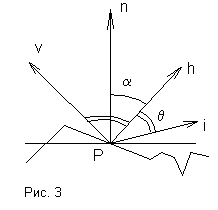Пусть n — нормаль к поверхности (ее средней линии), h — вектор нормали к микрограни и α — угол между ними,

α = arccos(n, h).

Поверхность будем описывать с помощью функции D(α), задающей плотность распределения случайной величины α (для идеально гладкой поверхности функция D(α) совпадает с δ- функцией Дирака).

Существует несколько распространенных моделей для функции D(α):

Гауссовское распределение

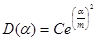, (19)

распределение Бекмена

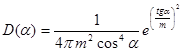. (20)

В этих моделях m характеризует степень неровности поверхности — чем меньше m, тем более гладкой является поверхность.

Рассмотрим отражение луча света, падающего в точку P вдоль направления, задаваемого вектором l. Пусть n — вектор внешней нормали к поверхности. Поскольку микрограни распределены случайным образом, то отраженный луч может уйти практически в любую сторону. Определим долю энергии, уходящей в заданном направлении v. Для того, чтобы луч отразился в этом направлении, необходимо,. Чтобы он попал на микрогрань, нормаль h к которой удовлетворяет соотношению

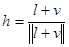. (21)

Доля энергии, которая отразится от микрограни, определяется коэффициентом Френеля 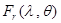, где

.

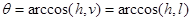Если поверхность состоит из множества микрограней, начинает сказываться затеняющее влияние соседних граней, которое обычно описывается с помощью следующей функции:

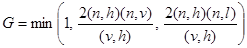. (22)

В этом случае интересующая нас доля энергии задается формулой

. (23)

Совершенно аналогично рассматривается преломление света поверхностью, состоящей из микрозеркал.

С использованием соотношения (23) можно построить формулу, полностью описывающую энергию (и отраженную, и преломленную) в заданном направлении. Для этого необходимо выпустить лучи во все возможные стороны и вычислить приходящую оттуда энергию, то есть в качестве вектора l можно рассматривать любой единичный вектор. Ясно, что на практике это невозможно.

Поэтому желательно взять алгоритм, отслеживающий лишь конечное число направлений, вносящих в искомую величину наибольший вклад.

Основная модель трассировки лучей

Введем некоторые ограничения на рассматриваемую сцену:

· будем рассматривать только точечные источники света;

· при трассировании преломленного луча будем игнорировать зависимость его направления от длины волны;

· будем считать освещенность объекта состоящей из диффузной и зеркальной частей (с заданными весами).

Для определения освещенности точки P определим сначала непосредственную освещенность этой точки от источников света (выпустив из нее лучи ко всем источникам).

Для определения вторичной освещенности выпустим их точки P один луч для отраженного направления и один луч для преломленного. Тем самым для определения освещенности точки необходимо будет отслеживать лишь небольшое количество лучей.

При этом неидеально зеркальные отражение лучей, идущих от других объектов, игнорируется.

Обычно для компенсации всех таких не учитываемых величин вводится так называемое фоновое освещение — равномерное освещение со всех сторон, которое ни от чего не зависит и не затеняется.

Тогда энергия, покидающая точку P в заданном направлении, задается следующей формулой:

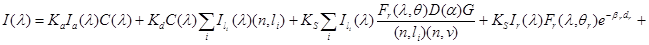
, (24)

где

— интенсивность фонового освещения;

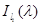— интенсивность i-го источника света;

— интенсивность, приходящая по отраженному лучу;

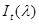— освещенность, приносимая преломленным лучом;

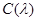— цвет в точке P;

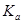— коэффициент фонового освещения;

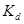— коэффициент диффузного освещения;

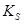— коэффициент зеркального освещения;

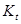— вклад преломленного луча;

— вектор внешней нормали в точке P;

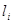— единичный вектор направления из точки P на i-ый источник света;

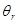— угол отражения (для отраженного луча);

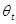— угол преломления;

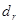— расстояние, пройденное отраженным лучом;

— расстояние, пройденное преломленным лучом;

— коэффициент ослабления для отраженного луча;

— коэффициент ослабления для преломленного луча.

К сожалению, эта модель, хотя и является достаточно физически корректной, слишком сложна для практического воплощения. Поэтому часто используются более простые модели, например модель Холла:

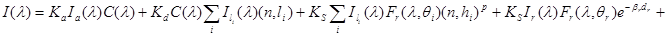
. (25)

Несмотря на то, что коэффициенты Френеля заметно влияют на степень реалистичности изображения, на практике их применяют очень редко. Дело в том, что их использование наталкивается на ряд серьезных препятствий, одним из которых является сложность вычисления, а другим — отсутствие точной информации о зависимости величин, входящих в состав формулы, от длины волны λ.

Существуют определенные методы интерполяции коэффициентов Френеля (например, линейная), которые в сочетании с табличным способом задания способны заметно ускорить процесс их вычисления, однако их рассмотрение выходит за рамки данной книги.

Далее будет рассматриваться модель Уиттеда:

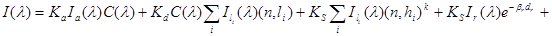
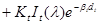. (26)

Замечание

Часто вместо члена 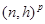используется .

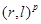DirectX API

Microsoft's DirectX API состоит из следующих групп:

• DirectDraw - прямой доступ к видеопамяти
• DirectSound - прямой доступ к звуковой карте
• DirectPlay - прямой доступ к сетевым возможностям для обеспечения multiplayer mode
• DirectInput - поддержка игровых устройств ввода

Все это предназначено для того, чтобы дать возможность программисту получить прямой доступ к различному (в основном игровому) железу. В данной статье дается пояснения к использованию интерфейса DirectDraw.

то такое DirectDraw

DirectDraw это обычный менеджер видеопамяти. Его основное назначение предоставить программисту прямой доступ к видеопамяти. Осуществлять такие операции, как копирование видео память -> видеопамять и т.п.. При этом напрямую могут использоваться возможности видеоконтроллера и освобождать от этих операций центральный процессор. Кроме того, DirectDraw напрямую использует и другие возможности Вашей видеокарты, как то спрайты, z - буферизацию и т.п.. Начиная с 5 версии DirectX дополнительно используются (во всяком случае декларируется использование) возможностей ММX - что позволяет за один цикл обрабатывать и передавать 64 бита видеоинформации.

Основной идеей DirectDraw является копирование видеопамяти в видеопамять, хотя также может поддерживаться и режим память->видеопамять. Что, конечно, является необходимым в мире видео карт с 1 метром видеопамяти.

оверхности DirectDraw - вид доступа к видеопамяти

Вашей основной задачей, как программиста, поместить в видеопамять столько изображений, необходимых для выполнения Вашей программы, как только возможно. Благо при использовании DirectDraw вся видеопамять доступна для Вас. Вы можете использовать ее для запоминания различных изображений (bitmap) , спрайтов и тп. Все эти видео элементы в терминологии DirectDraw называются поверхностями (surfaces). Основная последовательность при загрузке изображений следующая - Вы создаете поверхность(просто область видеопамяти (или системной памяти - если ресурсы видеопамяти исчерпаны)) , и загружаете в нее необходимое изображение.

DirectDraw обеспечен функциями определения доступной видео памяти - таким образом, Вы можете оптимизировать ее использование для конкретной видео карты. Минимальным для нормального использования DirectDraw представляется использование 2 M видео карт, хотя это субъективное мнение

Пример инициализации DirectDraw

LPDIRECTDRAW lpDD; // указатель на объект DirectDraw

// Функция инициализации объекта DirectDraw

// 1) Создаем Direct Draw Object

// 2) Устанавливаем вид доступа

// 3) Устанавливаем видео режим дисплея

BOOL DirectDrawInit(HWND hwnd)

{

HRESULT ddrval;

// Создание (получение) указателя на основной объект DirectDraw.

ddrval = DirectDrawCreate( NULL, &lpDD, NULL );

if( ddrval != DD_OK )

{

goto lError;

}

// DDSCL_EXCLUSIVE - полный доступ к видеопамяти и управлению видеорежимами

// требует флаг DDSCL_FULLSCREEN , т.е. Вы работаете со всем экраном сразу

// DDSCL_NORMAL - для обеспечения оконного доступа.

ddrval = lpDD->SetCooperativeLevel( hwnd, DDSCL_EXCLUSIVE | DDSCL_FULLSCREEN );

if( ddrval != DD_OK )

{

lpDD->Release();

//lError: здесь можно вставить код для оповещения пользователя о невозможности

return FALSE;

}

// Установим видео режим 800x600 256 цветов

// можно изменять, только если установлен флаг DDSCL_EXCLUSIVE

ddrval = lpDD->SetDisplayMode( 800, 600, 8);

if( ddrval != DD_OK )

{

lpDD->Release();

goto lError;

}

return TRUE;

}

Таким образом мы проинициализировали DirectDraw и изменили видео

Метод двоичного разбиения пространства

Существует другой, крайне элегантный способ упорядочивания граней.

Рассмотрим некоторую плоскость в объективном пространстве. Она разбивает множество всех граней на два непересекающихся множества (кластера), в зависимости от того, в каком полупространстве относительно плоскости эти грани лежат (будем считать, что плоскость не пересекает ни одну из этих граней).

При этом очевидно, что ни одна из граней, лежащих в полупространстве, не содержащем наблюдателя, не может закрывать собой ни одну из граней, лежащих в том же полупространстве, что и наблюдатель. Тем самым сначала необходимо вывести грани из дальнего кластера, а затем уже и из ближнего.

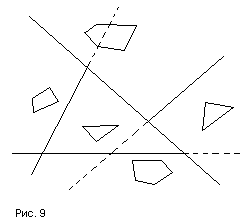Примени подобную технику для упорядочения граней внутри каждого кластера. Для этого построим разбиение граней каждого кластера на два множества очередной плоскостью; а затем для вновь полученных граней повторим процесс разбиения, и будем поступать так, до тех пор, пока в каждом получившемся кластере останется не более одной грани (рис. 9).

Обычно в качестве разбивающей плоскости рассматривается плоскость, проходящая через одну из граней (на самом деле при этом множество всех граней разбивается на 4 класса — лежащих на плоскости, пересекающих ее, лежащих в положительном полупространстве и лежащие в отрицательном полупространстве относительно этой плоскости). Все грани, пересекаемые плоскостью, разобъем вдоль этой плоскости.

В результате мы приходим к дереву разбиения пространства (Binary Space Partitioning), узлами которого являются грани. Каждый узел такого дерева можно представить в виде следующей структуры:

struct BSPNode

{

Facet *facet; // corresponding facet

Vector n; // normal to facet (plane)

Double d; // plane parameter

BSPNode *Left; // left subtree

BSPNode *Right; // right subtree

}

При этом Left указывает на вершину поддерева, содержащуюся в положительном полупространстве (p, n)>d, а Right — на поддерево, содержащееся в отрицательном полупространстве (p, n)<d.

Процесс построения дерева заключается в выборе грани, проведении через нее плоскости и разбиении множества всех граней. В этом процессе присутствует определенный произвол в выборе очередной грани. Существует два основных критерия для выбора:

· получить как можно более сбалансированное дерево;

· минимизировать количество разбиений.

К сожалению, эти критерии, как правило, являются взаимоисключающими, поэтому выбирается некоторый компромиссный вариант.

После того как это дерево построено, осуществляется построения изображения в зависимости от используемого проектирования. Ниже приводится процедура построения изображения для центрального проектирования с центром в точке C.

void DrawBSPTree(BSPNode *Tree)

{

if((Tree->n & c) > Tree -> d)

{

if (Tree -> Right != NULL) DrawBSPTree(Tree -> Right);

DrawFacet(Tree -> facet);

if (Tree -> Left != NULL) DrawBSPTree(Tree -> Left);

}

else

{

if (Tree ->Left != NULL) DrawBSPTree(Tree -> Left);

DrawFacet(Tree -> facet);

if (Tree -> Right != NULL) DrawBSPTree(Tree -> Right);

}

}

Одним из основных преимуществ этого метода является его полная независимость от положения центра проектирования, что делает его крайне удобным для построения серий изображений одной и той же сцены из разных точек наблюдения.

Удаление невидимых граней. Метод z-буфера

Одним из самых простых алгоритмов удаления невидимых граней и поверхностей является метод z-буфера (буфера глубины). В силу крайней простоты этого метода часто встречаются его аппаратные реализации.

Сопоставим каждому пикселу (x, y) картинной плоскости, кроме цвета, хранящегося в видеопамяти, его расстояние до картинной плоскости вдоль направления проектирования z(x, y) (его глубину).

Изначально массив глубин инициализируется +∞.

Для вывода на картинную плоскость произвольной грани она переводится в свое растровое представление на картинной плоскости и для каждого пиксела этой грани находится его глубина. В случае, если эта глубина меньше значения глубины, хранящегося в z-буфере, пиксел рисуется и его глубина заносится в z-буфер.

Замечание

Данный метод работает исключительно в пространстве картинной плоскости и не требует никакой предварительной обработки данных. Для вычисления глубины соседних пикселов при растровом разложении грани может использоваться вариант целочисленного алгоритма Брезенхейма.

Алгоритмы упорядочения

Метод, использованный ранее для построения графика функции двух переменных и заключающийся в последовательном выводе на экран всех граней в определенном порядке, может быть использован и для расчета более сложных сцен.

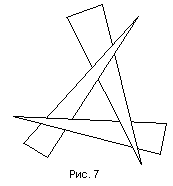Подход заключается в таком упорядочении граней, чтобы при их выводе в этом порядке получалось корректное изображение. Для этого необходимо, чтобы более дальние грани выводились раньше, чем более близкие.

Существуют различные методы построения такого упорядочения, однако часто встречаются такие случаи, когда заданные грани нельзя упорядочить (рис. 7). В подобных случаях необходимо произвести разбиение одной или нескольких граней, чтобы получившееся после разбиения множество граней можно было упорядочить.

Метод сортировки по глубине

Наиболее простым подходом к упорядочиванию граней является их сортировка по минимальному расстоянию до картинной плоскости (вдоль направления проектирования) с последующим выводом их в порядке приближения.

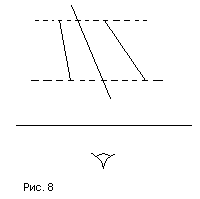Этот метод великолепно работает для ряда сцен, включая, например, построение изображения нескольких непересекающихся достаточно простых тел.

Однако возможны случаи, когда просто сортировка по расстоянию до картинной плоскости не обеспечивает правильного упорядочения граней (рис. 8); поэтому желательно после такой сортировки проверить порядок, в котором грани будут выводиться.

Предлагается следующий алгоритм этой проверки. Для простоты будем считать, что рассматривается параллельное проектирование вдоль оси Oz.

Перед выводом грани P следует убедиться, что никакая другая грань Q, проекция которой на ось Oz пересекается с проекцией грани P, не может закрываться гранью P. И если это условие выполнено, то грань P должна быть выведена раньше. Предлагаются следующие 5 тестов в порядке возрастания сложности проверки:

1. Пересекаются ли проекции этих граней на ось Ox?

2. Пересекаются ли их проекции на ось Oy?

3. Находится ли грань P по другую сторону от плоскости, проходящей через грань Q, чем начало координат (наблюдатель)?

4. Находится ли грань Q по ту же сторону от плоскости, проходящей через грань P, что и начало координат (наблюдатель)?

5. Пересекаются ли проекции этих граней на картинную плоскость?

Если хотя бы на один из этих вопросов получен отрицательный ответ, то считаем что эти две грани — P и Q упорядочены верно, и сравнением P со следующей гранью. В противном случае считаем, что эти грани необходимо поменять местами, для чего проверяются следующие тесты:

3’. Находится ли грань Q по другую сторону от плоскости, проходящей через грань P, чем начало координат?

4’. Находится ли грань P по ту же сторону от плоскости, проходящей через грань Q, что и начало координат?

В случае если ни один из этих тестов не позволяет с уверенностью решить, какую из этих двух граней нужно выводить раньше, то одна из них разбивается плоскостью, проходящей через другую грань. В этом случае вопрос об упорядочении оставшейся грани и частей разбитой грани легко решается.

Отсечение не лицевых граней

Рассмотрим многогранник, для каждой грани которого задан единичный вектор внешней нормали (рис. 3). Несложно заметить, что если вектор нормали грани n составляет с вектором l, задающим направление проектирование, тупой угол, то эта грань заведомо не может быть видна. Такие грани называются не лицевыми. В случае, когда соответствующий угол является острым, грань называется лицевой.

В случае параллельного проектирования условия на угол можно записать в виде

(n, l) ≤ 0,

поскольку направление проектирования l от грани не зависит.

При центральном проектировании с центром в точке C вектор проектирования для точки P будет равен

l = C – P.

Для определения того, является заданная грань лицевой или нет, достаточно взять произвольную точку P этой грани и проверить выполнение условия

(n, l) ≤ 0.

Знак этого скалярного произведения не зависит от выбора точки грани, а определяется тем, в каком полупространстве относительно плоскости, содержащей данную грань, лежит центр проектирования.

В случае, когда сцена представляет собой один выпуклый многогранник, удаление не лицевых граней полностью решает задачу удаления невидимых граней.

В общем случае предложенный подход хотя и не решает задачу полностью, но позволяет примерно вдвое сократить количество рассматриваемых граней.