Рекомендации к выполнению задания. Для решениязадачи N6необходимо знать следующие определения и свойства:
Для решениязадачи N6необходимо знать следующие определения и свойства:
1) Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений х из этого промежутка выполняется равенство F'(x)=f(x).
Если F(x)- первообразная для функции f(x) на промежутке X, то множество функций F(x)+C, где С - произвольная постоянная, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом
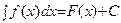
Свойства неопределенного интеграла:
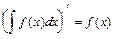 и
и 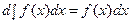
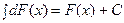
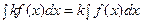
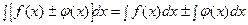
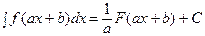
 4) Таблица основных интегралов и производных
4) Таблица основных интегралов и производных
| Производные и дифференциалы | Интегралы |
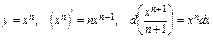 | 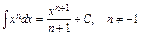 |
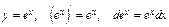 | 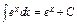 |
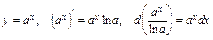 | 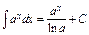 |
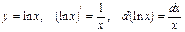 | 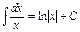 |
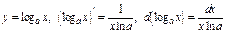 | 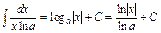 |
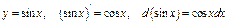 | 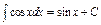 |
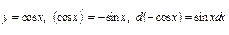 | 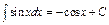 |
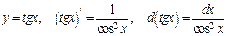 | 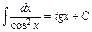 |
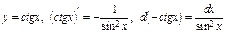 | 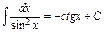 |
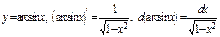 | 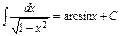 |
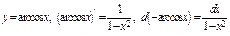 |  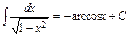 |
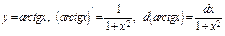 | 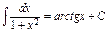 |
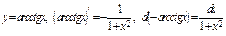 | 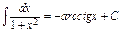 |
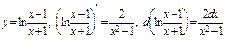 | 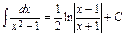 |
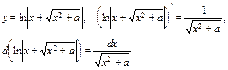 | 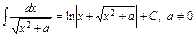 |
 Методы интегрирования.
Методы интегрирования.
а) Непосредственное интегрирование.
Пример 1.
Используя свойства неопределенного интеграла и таблицу простейших интегралов, найти интеграл
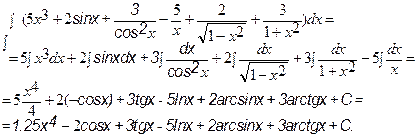
б) Метод подстановки.
Полагая х =j(t), где t - новая переменная, а j -непрерывно дифференцируемая функция, получим
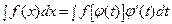 (1)
(1)
Функцию j выбирают таким образом, чтобы правая часть формулы (1) приобрела более удобный для интегрирования вид.
Пример 2.
Используя метод подстановки, найти интеграл



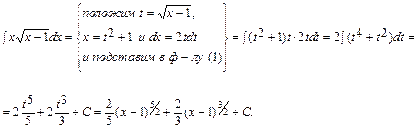
 Полезно знать, что:
Полезно знать, что:
-если интеграл содержит радикал 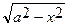 , то обычно полагают x=asint
, то обычно полагают x=asint 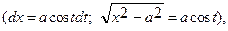 если интеграл содержит радикал
если интеграл содержит радикал 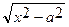 то полагают х = asect
то полагают х = asect
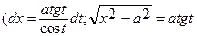 );
);
-если интеграл содержит радикал 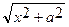 , то полагают х = atgt (dx=
, то полагают х = atgt (dx= 
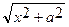 =asect);
=asect);
-если интеграл есть рациональная функция, содержащая sinx, cosx, то обычно используют подстановки t=tg 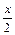
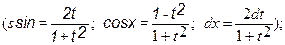
- если интеграл содержит радикал 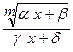 , и ad-gb¹0, то полагают
, и ad-gb¹0, то полагают 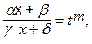
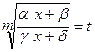 , x=
, x= 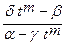 , dx=
, dx= 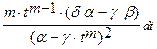
- если интеграл есть рациональная функция от eх, то полагают ex=t
(x=lnt, dx=dt/t).
в) Интегрирование по частям.
Если u=f(x) и v=w(x) - непрерывно дифференцируемые функции, то 
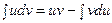 (2)
(2)
 Полезно знать, что
Полезно знать, что
-если подынтегральная функция есть произведение алгебраической и трансцендентной функций или двух трансцендентных функций, то интегрирование осуществляется только по частям.
(Трансцендентные функции: In x, sin x, cosx, arcsinx,arctg x, и т.п.);
- если производная трансцендентной функции является алгебраической функцией, то эта трансцендентная функция выбирается в качестве u в формуле (2).
((lnx)'= 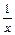
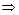 u=lnx);
u=lnx);
если производная трансцендентной функции есть трансцендентная функция, то в качестве u выбирается алгебраическая функция - для того, чтобы найти интеграл, формула (2) может применяться несколько раз;
в некоторых случаях с помощью (2) получают уравнение, из которого определяется искомый интеграл.
Пример 3.

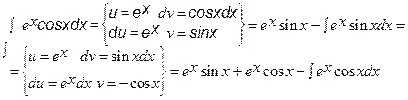
Следовательно, 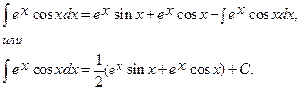
г) Частный случай - интегрирование рациональных функций вида
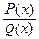 где Р(х) и Q(x) - многочлены.
где Р(х) и Q(x) - многочлены.
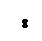 Интегрирование рациональных функций сводится к интегрированию многочленов и нахождению интегралов следующих четырех типов:
Интегрирование рациональных функций сводится к интегрированию многочленов и нахождению интегралов следующих четырех типов:
1. 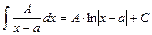
2. 
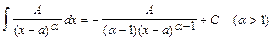
3. 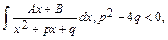 заменой
заменой 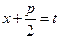 сводится к линейной комбинации интегралов:
сводится к линейной комбинации интегралов:
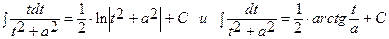
4. 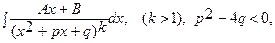 заменой
заменой 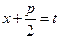 сводится к линейной комбинации интегралов:
сводится к линейной комбинации интегралов:
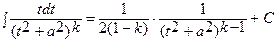 и
и 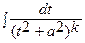 , (который можно вычислить по рекуррентной формуле).
, (который можно вычислить по рекуррентной формуле).
Пример решения задачи № 6.
Найти неопределенные интегралы. Результаты проверить дифференцированием.
а) 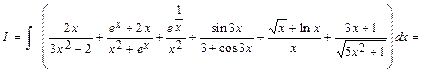
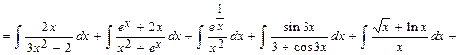
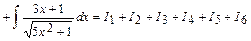 .
.
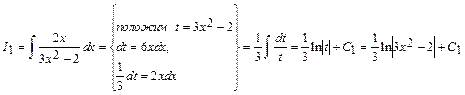
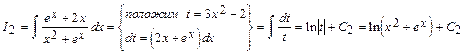
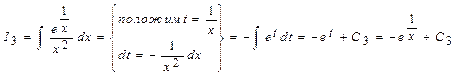
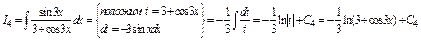
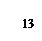
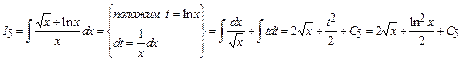
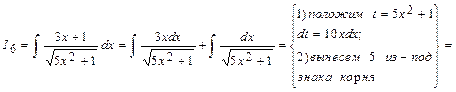
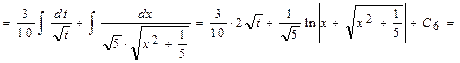
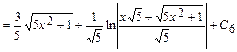 .
.
Следовательно, 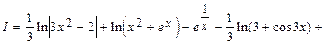
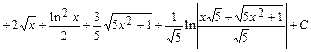 , где С=С1+С2+...+С6
, где С=С1+С2+...+С6
Проверим результат дифференцированием:
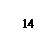
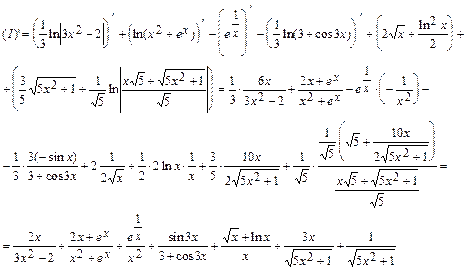
Полученное выражение равно исходной подынтегральной функции
б) 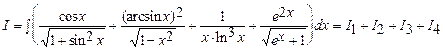
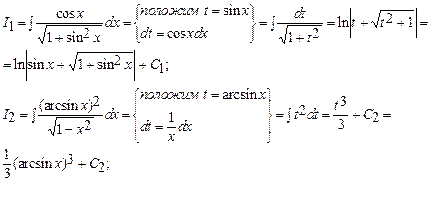
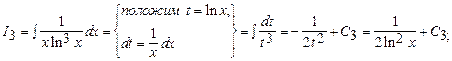
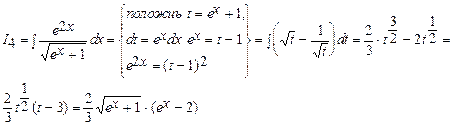
Следовательно,
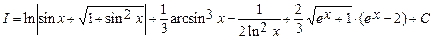
Проверим результат дифференцированием:
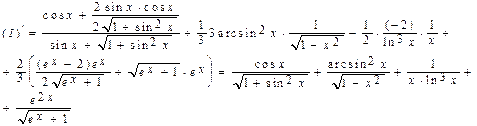
Полученное выражение равно исходной подынтегральной функции.
в) 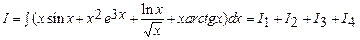
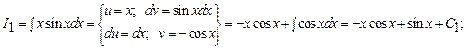
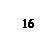
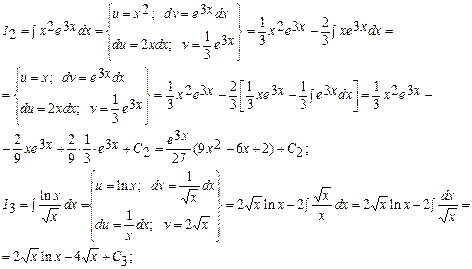
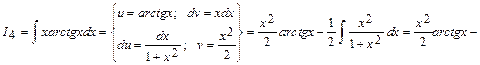
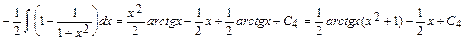 .
.
Следовательно,
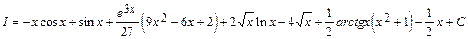
Проверим результат дифференцированием:
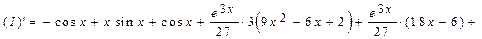
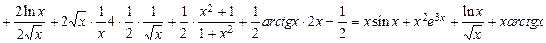
Полученное выражение равно исходному подынтегральному выражению.
Условия задачи 6.
а) 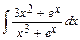 ; б)
; б) 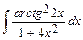 ;
;
2. а) 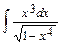 ; б)
; б) 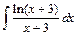 ;
;
3. а) 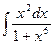 ; б)
; б) 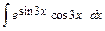 ;
;
4.а) 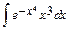 ; б)
; б) 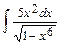 ;
;
5. а) 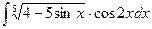 ; б)
; б) 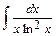 ;
;
 6
6  .а)
.а) 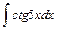 ; б)
; б) 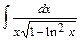 ;
;
7. а) 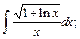 б)
б) 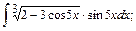
8. а) 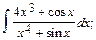 б)
б) 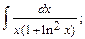
9.а) 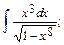 б)
б) 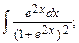
10.а) 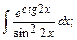 б)
б) 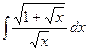 .
.
Задача 7. Найти определенный интеграл функции.
Для решения задачи № 7 необходимо знать следующее:
Формула Ньютона-Лейбница. Если 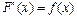 , то
, то

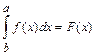

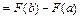
Свойства определенных интегралов.
а) 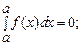
б) 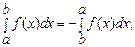
в) 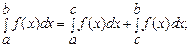
г) 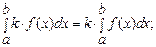
д) 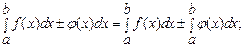
Замена переменной в определенном интеграле.
Пусть f(x) - непрерывная функция на [a, b]. Тогда если:
функция x=j(t) - дифференцируема на [a, b] и j¢(t) непрерывна на [ a,b];
множеством значений функции x=j(t) является отрезок
[a, b];
j(a)=a и j(b)=b, то справедлива формула
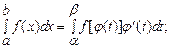
Интегрирование по частям в определенном интеграле.
Если функции u(x) и y(x) имеют непрерывные производные на отрезке [a, b] , то справедлива формула :
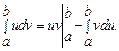
Пример решения задачи №7.
Вычислить по формуле Ньютона- Лейбница интегралы.
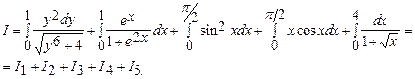
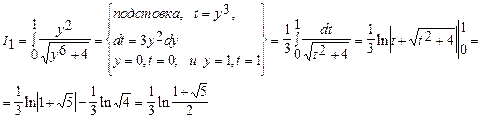
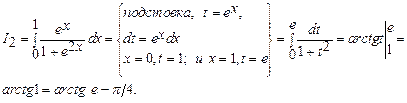
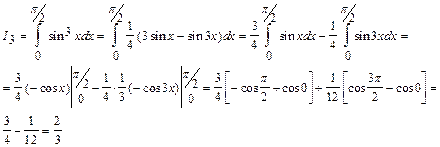
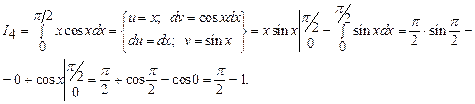
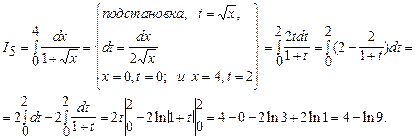
Следовательно,
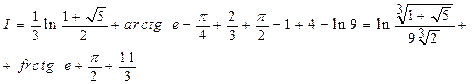
Условия задачи 7.
 1.
1. 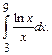
2. 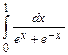 .
.
3. 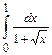 .
.
4. 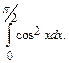
5. 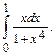
6. 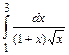

7. 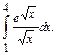
8. 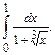
9. 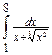 .
.
10. 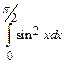 .
.
Задача 8.Для решения задачи №8 необходимо знать следующие понятия:
Дифференциальным уравнением первого порядка называется уравнение:
F(x,y,y')=0 (1)
связывающее независимую переменную х, искомую функцию y=j(x) и ее производную y'.
Уравнение вида y'=f(x,y) называется разрешенным относительно производной.
Решением уравнения (1) называется функция y=j(x), удовлетворяющая этому уравнению.
 Начальное условие для дифференциального уравнения первого порядка задается так:
Начальное условие для дифференциального уравнения первого порядка задается так:
y(x0)=y0 или y 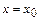 =y0
=y0
(оно означает, что при x=x0 функция у равняется заданному числу у0)
Общим решением уравнения (1) называется функция у=j(х,С), зависящая от одной произвольной постоянной С и удовлетворяющая уравнению (1) при любом значении С.
Частным решением уравнения (1) называется любая функция у=j(х,С), которая получается из общего решения у=j(х,с) при значении с=с0.
 Решением задачи Коши называется частное решение уравнения (1), удовлетворяющее заданным начальным условиям
Решением задачи Коши называется частное решение уравнения (1), удовлетворяющее заданным начальным условиям
y 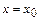 =y0
=y0
Линейным дифференциальным уравнением первого порядка называется уравнение, в котором искомая функция у и ее производная у' находятся в первой степени:
у'+p(x)y=q(x) (2)
или
a(x)y'+(x)y=c(x) (2')
где p(x), q(x), a(x), b(x), c(x) - заданные непрерывные функции от х.
Общее решение дифференциального уравнения (2) имеет вид:
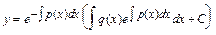 (3)
(3)
Пример решения задачи № 8.
Найти общее решение дифференциального уравнения xy+y=2xlnx+x,и частное решение, удовлетворяющее начальному условию y0=5 при x0=1.
Решение.
Данное уравнение является линейным, так как y и y' входят в него в первой степени. Запишем это уравнение в виде (2):
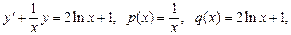
 Подставим в формулу (3) общего решения значения p(x) и q(x):
Подставим в формулу (3) общего решения значения p(x) и q(x):
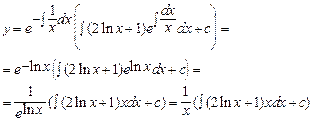
Применим формулу интегрирования по частям 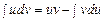 к интегралу
к интегралу
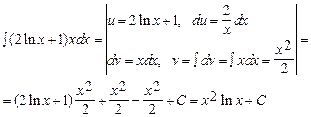
Тогда общее решение исходного дифференциального уравнения имеет вид:
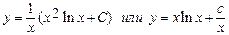
Найдем теперь частное решение уравнения , удовлетворяющее заданному начальному условию y0=5 при x0=1.
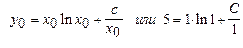 , откуда следует, что С=5.
, откуда следует, что С=5.
Решение поставленной задачи Коши 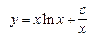 .
.
Ответ: общее решение дифференциального уравнения 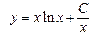 ; частное решение , удовлетворяющее начальному условию y0=5 при x0=1:
; частное решение , удовлетворяющее начальному условию y0=5 при x0=1: 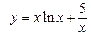 .
.
Условия задачи 8.
Найти общее решение дифференциального уравнения 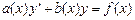 и частное решение, удовлетворяющее начальному условию y=y0 при x=x0.
и частное решение, удовлетворяющее начальному условию y=y0 при x=x0.
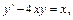
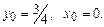
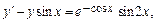
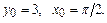
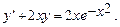
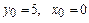
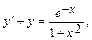
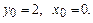
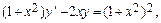
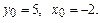
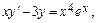
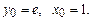
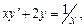
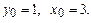
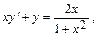
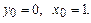
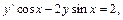
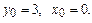
10. 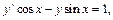
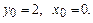
Задача 9. Для решения задачи 9необходимо знать следующие понятия:
пусть задана числовая последовательность 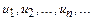
Числовым рядом называется выражение вида: 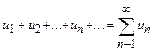 .
.
При этом числа 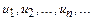 называются членами ряда, а un общим членом ряда.
называются членами ряда, а un общим членом ряда.
Сумма конечного числа n первых членов ряда называется n-й частичной суммой ряда и обозначается Sn :
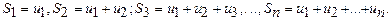
Числовой ряд (8) называется сходящимся, если существует конечный предел последовательности частичных сумм 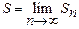 и этот предел S называется суммой ряда.
и этот предел S называется суммой ряда.
Если 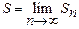 не существует или бесконечен ,то ряд (8) называется расходящимся .
не существует или бесконечен ,то ряд (8) называется расходящимся .
Теорема 1 (необходимый признак сходимости ряда). Если ряд (8)
сходится, то предел общего члена ряда равен нулю: 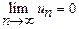 .
.
Числовой ряд 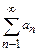 называется положительным, если все его члены положительны: an>0,n=1,2,...
называется положительным, если все его члены положительны: an>0,n=1,2,...
Теорема 2 (признак Даламбера). Если в ряде с положительными членами 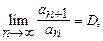 то 1) ряд сходится при D<1;
то 1) ряд сходится при D<1;
ряд расходится при D>1.
 В случае D=1 ответа на вопрос о сходимости или расходимости ряда теорема не дает.
В случае D=1 ответа на вопрос о сходимости или расходимости ряда теорема не дает.
Теорема 3 (предельный признак сравнения положительных рядов). Если для общих членов двух положительных рядов 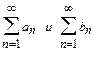
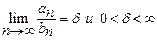 ,то оба ряда сходятся или расходятся одновременно.
,то оба ряда сходятся или расходятся одновременно.
Замечание. В качестве рядов сравнения используются либо ряд 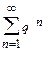 , который сходится при 0< q <1 b и расходится при q>1, либо обобщенный гармонический ряд
, который сходится при 0< q <1 b и расходится при q>1, либо обобщенный гармонический ряд 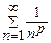 , который сходится при p>1
, который сходится при p>1
и расходится при p<1.
Числовой ряд называется знакочередующимся, если любые его два ряда соседних члена имеют противоположные знаки:
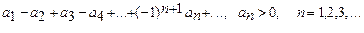 (9)
(9)
Теорема 4 (признак Лейбница).
Если члены знакочередующегося ряда (9) по абсолютной величине монотонно убывают и 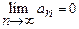 , то ряд (9) сходится, его сумма положительна и не превышает первого члена.
, то ряд (9) сходится, его сумма положительна и не превышает первого члена.
Степенным рядом называется ряд вида
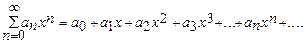 (10)
(10)
где а0,а1,а3,...,аn,... - постоянные числа, называемые коэффициентами ряда.
Если степенной ряд сходится при всех x, удовлетворяющих неравенству 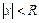 и расходится при
и расходится при 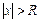 , то число R называется радиусом сходимости степенного ряда, а интервал (-R,R) называется интервалом сходимости ряда.
, то число R называется радиусом сходимости степенного ряда, а интервал (-R,R) называется интервалом сходимости ряда.
 Радиус сходимости степенного ряда (10) определяется по формуле
Радиус сходимости степенного ряда (10) определяется по формуле
Замечание 1. Внутри интервала сходимости степенной ряд сходится, а на концах интервала в точках x=R и x=-R может либо сходится ,либо расходится.
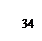 Теорема 5. Степенной ряд внутри интервала сходимости можно почленно дифференцировать и интегрировать, при этом радиус сходимости не меняется, но сходимость ряда на концах интервала может меняться.
Теорема 5. Степенной ряд внутри интервала сходимости можно почленно дифференцировать и интегрировать, при этом радиус сходимости не меняется, но сходимость ряда на концах интервала может меняться.
Пример решения задачи 9.
а) Написать три первых члена степенного ряда по заданному общему члену 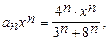 найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
Решение.
Запишем три первых члена степенного ряда 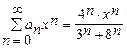 .
.
При n=0 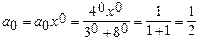 .
.
При n=1 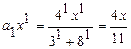 .
.
При n=2 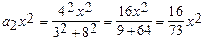 .
.
Найдем радиус сходимости степенного ряда: 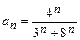 ;
;
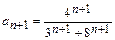 и
и
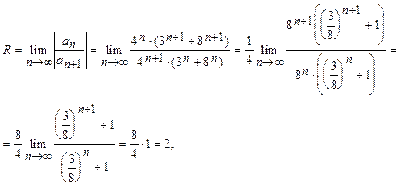
следовательно, промежуток (-2;2) является интервалом сходимости ряда.
Исследуем поведение ряда на концах интервала сходимости в точках x=-2 и x=2.
При x=-2: 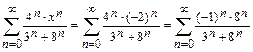 .
.
Модуль общего члена ряда 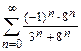
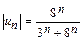 и
и 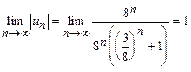 ,
,
поэтому общий член ряда не стремится к нулю и на основании необходимого признака сходимости ряд расходится.
При x=2: 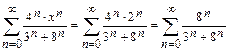
и общий член последнего ряда не стремится к нулю: 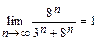 ,
,
поэтому ряд расходится. На обоих концах интервала сходимости ряд расходится.
Ответ: интервал сходимости степенного ряда (-2;2) на концах ин -
тервала сходимости ряд расходится.
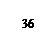
б) Найти интервал сходимости ряда 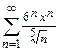 и исследовать его сходимость на концах этого интервала.
и исследовать его сходимость на концах этого интервала.
Решение.
Найдем радиус сходимости степенного ряда:
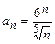 ,
, 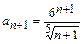 , и
, и
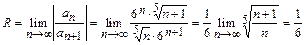
следовательно, множество 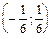 является интервалом сходимости ряда.
является интервалом сходимости ряда.
Исследуем поведение ряда на концах интервала сходимости в точках 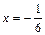 и
и 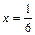 :
:
при 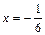 :
: 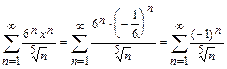
Получился числовой знакочередующийся ряд, который сходится по признаку Лейбница (члены ряда монотонно убывают по абсолютной величине и общий член ряда стремится к нулю).
При x= 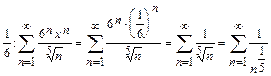
Полученный ряд расходится как обобщенный гармонический ряд с показателем 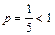 . На
. На 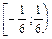 ряд сходится.
ряд сходится.
Условия задачи 9.
Найти интервал сходимости ряда с общим членом 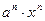 и исследовать его сходимость на концах этого интервала.
и исследовать его сходимость на концах этого интервала.
1. 
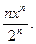
2. 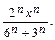
3. 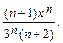
4. 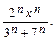
5. 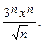
6. 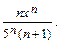
7. 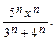
8. 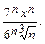
9. 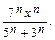
10. 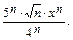

Приложение 1
Рег.№____
«__»_______201__г.
КОНТРОЛЬНАЯ РАБОТА
по математике
Выполнил студент 1 курса направления
«________________________________________»
________________________________________________________________
(Ф.И.О.)
группа ___________________
Домашний адрес____________________________________________
Телефон_________________________________
Проверил _________________________________________
(Ф.И.О. преподавателя)
К.р._______________________________________________
(зачтена, не зачтена)
Дата_____________________
