Для студентов 2 курса заочного факультета
Утверждаю
И.о. заведующего кафедрой
«ИиМОТС»
Казаков Н.Н.
«___» 2017 г.
Вопросы к зачёту
по дисциплине «Теория вероятностей и математическая статистика»
для студентов 2 курса заочного факультета
(летняя экзаменационная сессия 2016/17 уч. года)
Раздел «Теория вероятностей»
1. Вероятностный эксперимент. Пространство элементарных событий.
2. Операции над событиями.
3. Вероятность случайного события. Относительная частота случайного события. Понятие вероятности случайного события. Аксиомы теории вероятностей.
4. Классический метод вычисления вероятностей. Элементы комбинаторики.
5. Геометрический метод вычисления вероятностей.
6. Свойства вероятностей случайного события.
7. Теоремы сложения и умножения вероятностей. Условная вероятность. Независимость событий.
8. Формула полной вероятности. Формула Байеса.
9. Испытания Бернулли. Схема Бернулли. Формула Бернулли.
10. Предельная теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа.
11. Понятие одномерной случайной величины (СВ).
12. Закон распределения СВ.
13. Функция распределения СВ и ее свойства.
14. Функция плотности распределения СВ и ее свойства.
15. Числовые характеристики СВ. Математическое ожидание, дисперсия, мода, медиана, среднеквадратическое отклонение, коэффициент асимметрии, коэффициент эксцесса.
16. Законы распределения СВ. Биномиальный закон распределения.
17. Законы распределения СВ. Закон распределения Пуассона.
18. Законы распределения СВ. Геометрический закон распределения.
19. Законы распределения СВ. Равномерный закон распределения.
20. Законы распределения СВ. Показательный закон распределения. Лемма об «отсутствии памяти» у показательного распределения.
21. Законы распределения СВ. Нормальный закон распределения.
22. Законы распределения СВ. Закон распределения Эрланга.
23. Предельные теоремы теории вероятностей.
24. Понятие многомерной СВ.
25. Функция распределения двумерной СВ.
26. Функция плотности распределения двумерной СВ.
27. Понятие зависимости многомерных СВ.
28. Числовые характеристики двумерной СВ.
Раздел «Математическая статистика»
1. Предмет и задачи математической статистики. Генеральная совокупность и выборочный метод.
2. Статистический ряд. Статистическое распределение СВ. Эмпирическая функция распределения. Графическое изображение статистических рядов.
3. Распределения СВ. Распределение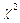 
Пирсона.
4. Распределения СВ. Распределение Стьюдента.
5. Распределения СВ. Распределение Фишера.
6. Точечные оценки числовых характеристик и параметров распределения СВ. Классификация точечных оценок.
7. Интервальные оценки числовых характеристик СВ. Схема построения интервальных оценок параметров распределения и числовых характеристик СВ.
8. Построение доверительного интервала для математического ожидания СВ, имеющей нормальный закон распределения с известным среднеквадратическим отклонением.
9. Построение доверительного интервала для математического ожидания СВ, имеющей нормальный закон распределения с неизвестным среднеквадратическим отклонением.
10. Построение доверительного интервала для среднеквадратического отклонения СВ, имеющей нормальное распределения.
11. Статистическая проверка параметрических гипотез. Статистический критерий значимости. Ошибки, совершаемые при проверке статистических гипотез.
12. Проверка гипотезы о значении математического ожидания СВ, имеющей нормальный закон распределения с известным среднеквадратическим отклонением.
13. Проверка гипотезы о значении математического ожидания СВ, имеющей нормальный закон распределения с неизвестным среднеквадратическим отклонением.
14. Проверка гипотезы о значении математического ожидания двух независимых СВ, имеющих нормальный закон распределения с известным среднеквадратическим отклонением.
15. Проверка гипотезы о значении математического ожидания двух независимых СВ, имеющих нормальный закон распределения с неизвестными, но равными среднеквадратическими отклонениями.
16. Статистическая проверка непараметрических гипотез. Критерий «согласия» Пирсона ( ).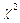
17. Статистическая проверка непараметрических гипотез. Критерий «согласия» Колмогорова.
18. Элементы регрессионного и корреляционного анализа. Зависимость между двумя СВ.
19. Элементы регрессионного и корреляционного анализа. Подбор уравнения регрессии.
20. Определение параметров уравнения регрессии методом наименьших квадратов (МНК).
21. Пошаговый регрессионный анализ.
22. Коэффициенты корреляции и детерминации.
23. Проверка значимости коэффициентов корреляции и детерминации.
Составил В.Е. Евдокимович