Опр.Полным дифференциалом ФНП наз. главная часть приращения функции линейная по приращению всех аргументов.
Для z = f(x,y)приращение функции представим в виде :
 z = A
z = A  x + B
x + B  y +
y + 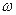 (
(  x,
x,  y),где
y),где 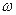 (
(  x,
x,  y) –б.м.в. более высокого порядка чем
y) –б.м.в. более высокого порядка чем

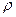 =
=  , т.е. расстояние между М и М0 при М
, т.е. расстояние между М и М0 при М 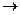 М0 . Если такое разложение существует, то функция z = f(x,y)наз. дифференцируемой, а линейная по
М0 . Если такое разложение существует, то функция z = f(x,y)наз. дифференцируемой, а линейная по  xи
xи  yчасть разложения есть полный дифференциал функции : dz = A
yчасть разложения есть полный дифференциал функции : dz = A  x + B
x + B  y .
y .
Необходимое и достаточное условие дифференцируемости функции :
Функция дифференцируема в точке, если существуют её частные производные в этой точке и они непрерывны, причем, ¶z/ ¶x = А , ¶z/ ¶y = B
¶z/ ¶x = lim (A  x +
x + 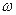 (
(  x, 0) )/
x, 0) )/  x = A + lim
x = A + lim 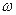 (
(  x, 0) /
x, 0) /  x = A
x = A
 x
x 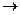 0
0  x
x 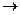 0
0
Т.о., полный дифференциал ФНП есть сумма частных дифференциалов
dz = (¶z/ ¶x) dx + (¶z/ ¶y) dy(5)
Пр. Найти полный дифференциал функции z = xy3 , u = xyz
Частные производные высших порядков.
Частные производные ¶z/ ¶x = f `x(x,y), ¶z/ ¶y = f `y(x,y)являются функциями от х, у .
Если они дифференцируемы, то для них получаем 4 производных второго порядка
¶ 2z/ ¶x2 = ¶ (¶z/ ¶x)/ ¶x , ¶ 2z/ ¶x¶y = ¶(¶z/ ¶x)/ ¶y ,
¶ 2z/ ¶y2 = ¶ (¶z/ ¶y)/ ¶y , ¶2z/¶x¶y = ¶(¶z/ ¶y)/ ¶x
Опр.Частной производной n – ого порядка наз. частная производная первого порядка от частной производной n – 1порядка.
Теорема. Если частные производные, отличающиеся только порядком дифференцирования, непрерывны в точке М , то они равны между собой.
Например, ¶2z/¶x¶y = ¶2z/¶y¶x .
Пр. Найти производные 1-ого, 2-ого порядка от функции z = x3y + y4
Опр.Дифференциалом 2-ого порядка функции z = f(x,y)наз. дифференциал от ее дифференциала 1-ого порядка (при условии dx, dy -константы)
d2z =d(dz) =d[(¶z/¶x)dx + (¶z/¶y) dy] = (¶ 2z/ ¶x2)dx2 + 2(¶ 2z/¶x¶y)dx dy + (¶ 2z/¶y2)dy2 ( 6 )
Производные сложных функций.
Пусть для z = f(x,y)переменные х , уявляются функциями параметра t : x = x(t), y = y(t) .Тогда функция z = f(x(t), y(t))является сложной функцией параметра tи ее производная по tявляется отношением полного дифференциала dzк dt(по опр. Ньютона),т.е.
 ( 7 )
( 7 )
Пр. z = y ln x2 , x = sin t , y = cos t , dz/ dt = ?
Если в функции z = f(x,y)аргументы связаны дополнительным условием y = y(x),то независимым аргументом оказывается только х.Для вычисления производнойdz/dxсоставим отношение полного дифференциала dzк dx
 =
=  ( 8 )
( 8 )
Геометрически это означает, что мы находим производную вдоль линии пересеченияповерхности z = f(x,y)c некоторой цилиндрической поверхностьюy = y(x) | | оси Оz .
Пр. z = y x ; y = cos x ; dz/dx = ?
Если для z = f(x,y) имеем x = x(u, v) , y = y(u, v), т.е. дополнительная цилиндрическая поверхность определяется двумя параметрами, и ¶z/¶u = ? , ¶z/¶v = ?, то отношение полного дифференциала dz к du при условии v – const приводит к формуле
 ;
;  ( 9 )
( 9 )
Пр. z = x2 + 2y2 ; x = 4u + 3v ; y = 2u – 5v ; ¶z/du =? , ¶z/¶v = ?
Производные неявных функций.
Пусть дана неявная функция F(x, y) = 0 ,сложным образом связывающая аргумент х и у = у(х) .Надо найти производную dy/ dx .
Полный дифференциал функции F(x,y)разделим на dx
 Þ
Þ  ( 10 )
( 10 )
Пр. exp x2 + x y2 = 0 ; dy/ dx = ? .ПустьF(x,y) = exp x2 + x y2 ,тогда
¶F/¶x = 2x exp x2 + y2 ; ¶F/¶y = 2 xy ; dy/dx = - (2x exp x2 + y2) / 2xy
Пусть дана неявная функция F(x,y,z) = 0 ,сложным образом связывающая аргументы х, уи z = z(x, y).Надо найти производные ¶z/¶x , ¶z/¶y.
