Определения и обозначения, используемые в работе. Определение 1.1.1. Группа, являющая прямым произведением групп, изоморфных , называется элементарной абелевой -группой.
Определение 1.1.1. Группа, являющая прямым произведением групп, изоморфных 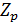 , называется элементарной абелевой -группой.
, называется элементарной абелевой -группой.
Определение 1.1.2. Группа  называется бипримарной, если
называется бипримарной, если 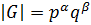 , где
, где 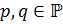 ,
, 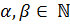 .
.
Определение 1.1.3. Группой называется непустое множество  с бинарной алгебраической операцией
с бинарной алгебраической операцией  , удовлетворяющей следующим
, удовлетворяющей следующим
требованиям:
1) операция ∘ ассоциативна, т.е. 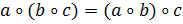 ,для всех
,для всех 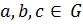 ;
;
2) в  существует нейтральный элемент относительно операции ∘, то есть такой элемент
существует нейтральный элемент относительно операции ∘, то есть такой элемент 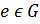 что
что 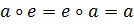 для всех
для всех 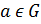 ;
;
3) каждый элемент обладает симметричным относительно операции ∘, то есть для любого 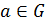 существует такой элемент
существует такой элемент 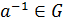 что a∘
что a∘ 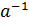 =
= 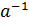 ∘
∘ 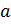 =
= 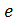 .
.
Определение 1.1.4. Группа с коммутативной операцией называется абелевой.
Определение 1.1.5. Если число элементов группы  конечно, то
конечно, то  называется конечной группой; число элементов в
называется конечной группой; число элементов в  называется порядком группы
называется порядком группы  и обозначается
и обозначается 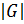 .
.
Определение 1.1.6.Непустое подмножество 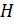 группы
группы  называется подгруппой группы
называется подгруппой группы  и обозначается
и обозначается 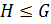 , если
, если 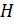 является группой относительно той же операции, что и группа
является группой относительно той же операции, что и группа  .
.
Определение 1.1.7. Подгруппа 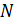 группы
группы  называется нормальной подгруппой и обозначается
называется нормальной подгруппой и обозначается 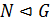 , если выполняется такое равенство
, если выполняется такое равенство 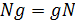 ,
, 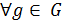 .
.
Определение 1.1.8. Подгруппа 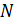 группы
группы  называется нормальной, если
называется нормальной, если 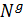 =
= 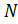 ,
, 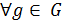 .
.
Определение 1.1.9. 1. Пусть  — группа, 1 — единичный элемент группы
— группа, 1 — единичный элемент группы  . Подгруппа
. Подгруппа 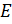 ={1} называется единичной подгруппой группы
={1} называется единичной подгруппой группы  (обычно единичную подгруппу обозначают 1, т.е. пишут 1≤
(обычно единичную подгруппу обозначают 1, т.е. пишут 1≤ 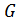 )
)
2. Подгруппы 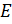 и
и  называются тривиальными подгруппами группы
называются тривиальными подгруппами группы 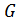 .
.
Определение 1.1.10. Неединичная группа  называется простой, если
называется простой, если
она не имеет нетривиальных нормальных подгрупп.
Определение 1.1.11. Нормальная подгруппа 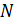 группы
группы  называется минимальной нормальной подгруппой, если
называется минимальной нормальной подгруппой, если 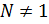 и
и 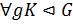 справедливо: если 1 ⊆
справедливо: если 1 ⊆ 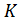 ⊆
⊆ 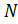 , то
, то 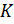 =1 или
=1 или 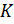 =
= 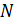 и обозначается
и обозначается 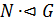 .
.
Другими словами, не существует такой нормальной подгруппы 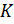 группы
группы  , чтобы 1⊂
, чтобы 1⊂ 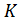 ⊂
⊂ 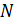 .
.
Определение 1.1.12. Подгруппа 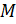 группы
группы  называется максимальной подгруппой группы
называется максимальной подгруппой группы  и обозначается
и обозначается 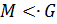 , если
, если 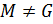 и ∀
и ∀ 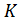 ≤
≤ 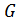 справедливо: если
справедливо: если 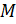 ⊆
⊆ 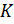 ⊆
⊆ 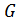 , то
, то 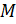 =
= 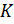 или
или 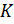 =
=  .
.
Другими словами, 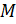 <∙
<∙  , если M≠
, если M≠  и не существует такой подгруппы
и не существует такой подгруппы 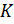 группы
группы  , что
, что 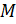 ⊂
⊂ 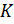 ⊂
⊂ 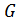 .
.
Определение 1.1.13. Подгруппой Фраттини группы  называется пересечение всех максимальных подгрупп группы
называется пересечение всех максимальных подгрупп группы  , если они существуют и сама группа
, если они существуют и сама группа  в противном случае и обозначается
в противном случае и обозначается 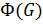 , то есть
, то есть 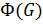 =∩
=∩ 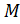 ,где
,где 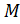 <∙
<∙  или
или 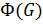 =
=  .
.
Определение 1.1.14. Неединичная группа  называется -простой, где
называется -простой, где 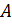 ⊆
⊆ 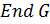 , если
, если  не содержит нетривиальных
не содержит нетривиальных 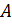 -допустимых подгрупп.
-допустимых подгрупп.
Определение 1.1.15. 1. Неединичная группа  называется простой, если
называется простой, если  не содержит нетривиальных
не содержит нетривиальных 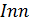 -допустимых подгрупп (нормальных).
-допустимых подгрупп (нормальных).
2. Неединичная группа  называется характеристически простой, если
называется характеристически простой, если
 не содержит нетривиальных
не содержит нетривиальных 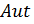 -допустимых подгрупп (характеристических).
-допустимых подгрупп (характеристических).
Определение 1.1.16. Пусть  — группа,
— группа, 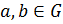 . Коммутатором элементов
. Коммутатором элементов 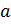 и
и 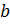 группы
группы  называется элемент
называется элемент 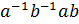 и обозначается
и обозначается 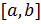 , т.е.
, т.е. 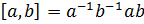 .
.
Определение 1.1.17. Коммутантом группы 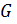 называется подгруппа
называется подгруппа 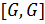 группы
группы  и обозначается
и обозначается 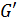 ,
, 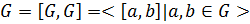 .
.
Определение 1.1.18. Группа  называется примарной, если её порядок равен степени некоторого простого числа.
называется примарной, если её порядок равен степени некоторого простого числа.
Определение 1.1.19. Пусть 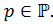 Группа
Группа  называется -группой, если
называется -группой, если 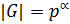 , где
, где 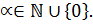
Определение 1.1.20. 1) Конечная последовательность подгрупп группы  вида
вида 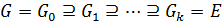 (1) называется рядом группы
(1) называется рядом группы  .
.
2) Конечная последовательность подгрупп группы  вида
вида 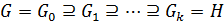 (2) называется цепью группы
(2) называется цепью группы  , соединяющей
, соединяющей  с
с 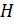 , или
, или 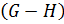 -цепью.
-цепью.
3) Число 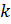 называется длиной ряда (1) или цепи (2). Подгруппы
называется длиной ряда (1) или цепи (2). Подгруппы 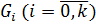 называются членами ряда (1) или цепи (2).
называются членами ряда (1) или цепи (2).
Определение 1.1.21. 1) Ряд (цепь) группы  называется нормальным рядом (цепью), если
называется нормальным рядом (цепью), если 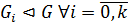 .
.
2) Ряд (цепь) группы  называется субнормальным рядом (цепью), если
называется субнормальным рядом (цепью), если 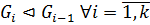 .
.
3) Факторгруппы 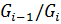 нормального (субнормального) ряда называются нормальными (субнормальными) факторами группы
нормального (субнормального) ряда называются нормальными (субнормальными) факторами группы  .
.
Определение 1.1.22. 1) Нормальный ряд группы  без повторений членов называется главным рядом группы
без повторений членов называется главным рядом группы  , если он не допускает дальнейшего уплотнения нормальными подгруппами, т.е.
, если он не допускает дальнейшего уплотнения нормальными подгруппами, т.е. 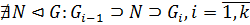 .
.
2) Субнормальный ряд группы  без повторений членов называется композиционным рядом группы
без повторений членов называется композиционным рядом группы  , если он не допускает дальнейшего уплотнения субнормальными подгруппами, т.е.
, если он не допускает дальнейшего уплотнения субнормальными подгруппами, т.е. 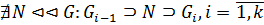 .
.
3) Фактор главного (композиционного ряда) называется главным (композиционным) фактором.
Определение 1.1.23. Два субнормальных ряда группы  называются изоморфными, если они имеют одинаковую длину и между их факторами существует биективное соответствие, при котором соответствующие факторы изоморфны.
называются изоморфными, если они имеют одинаковую длину и между их факторами существует биективное соответствие, при котором соответствующие факторы изоморфны.
Определение 1.1.24. Конечная группа  называется нильпотентной, если каждая силовская подгруппа группы
называется нильпотентной, если каждая силовская подгруппа группы  нормальна в
нормальна в  .
.
Определение 1.1.25. Конечная группа  называется нильпотентной, если
называется нильпотентной, если  является прямым произведением своих силовских подгрупп.
является прямым произведением своих силовских подгрупп.
Определение 1.1.26. Группа  называется нильпотентной, если
называется нильпотентной, если  обладает центральным рядом, то есть таким нормальным рядом, все факторы которого центральны.
обладает центральным рядом, то есть таким нормальным рядом, все факторы которого центральны.
Через 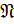 обозначается множество всех конечных нильпотентных групп.
обозначается множество всех конечных нильпотентных групп.
Определение 1.1.27. 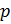 -замкнутой называют группу с нормальной силовской -подгруппой.
-замкнутой называют группу с нормальной силовской -подгруппой.
Определение 1.1.28. Группа 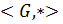 называется абелевой, если операция
называется абелевой, если операция  коммутативна на
коммутативна на  , т.е.
, т.е. 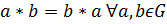 .
.
Определение 1.1.29. Группа 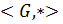 называется конечной, если она состоит из конечного числа элементов.
называется конечной, если она состоит из конечного числа элементов.
Определение 1.1.30. 1) Порядком конечной группы  называется число его элементов и обозначается
называется число его элементов и обозначается 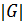 .
.
2) 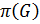 — совокупность всех простых делителей порядка группы
— совокупность всех простых делителей порядка группы  , т.е.
, т.е. 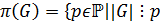 }.
}.
Определение 1.1.31. Пусть 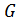 — группа,
— группа, 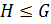 .Множество
.Множество 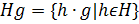 называется правым смежным классом группы
называется правым смежным классом группы  по подгруппе
по подгруппе 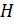 с представителем
с представителем 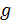 .
.
Аналогично 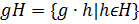 — левый смежный класс группы
— левый смежный класс группы  по подгруппе
по подгруппе 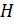 с представителем
с представителем 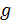 .
.
Определение 1.1.32. Пусть 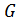 — группа,
— группа, 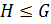 . Индексом подгруппы
. Индексом подгруппы 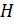 в группе
в группе  называется число смежных классов в разложении группы
называется число смежных классов в разложении группы  по подгруппе
по подгруппе 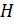 и обозначается
и обозначается 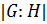 .
.
Обозначение 1.1.33. Пусть 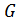 — группа,
— группа, 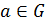 ,
, 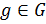 . Тогда
. Тогда 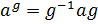 .
.
Обозначение 1.1.34.Пусть 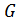 — группа,
— группа, 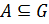 ,
, 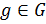 . Тогда
. Тогда 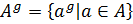 .
.
Определение 1.1.35. 1. Пусть 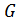 — группа,
— группа, 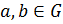 . Элемент
. Элемент 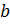 называется сопряжённым к элементу
называется сопряжённым к элементу 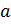 , если
, если 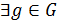 , такой что
, такой что 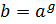 .
.
2. Пусть 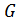 — группа,
— группа, 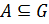 ,
, 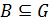 . Множество
. Множество 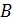 называется сопряжённым к множеству
называется сопряжённым к множеству 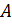 , если
, если 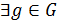 , такой что
, такой что 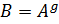 .
.
Используемые результаты
Лемма 1.2.1. Пусть 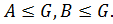 Тогда справедливы следующие утверждения:
Тогда справедливы следующие утверждения:
1) 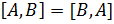 ;
;
2) 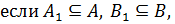 то
то 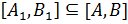 ;
;
3) если 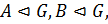 то
то 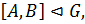 и
и 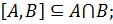
4) 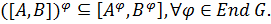
Лемма 1.2.2. 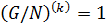 тогда и только тогда, когда
тогда и только тогда, когда 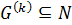 .
.
Лемма 1.2.3. Если 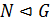 ,
, 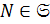 ,
, 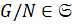 , то
, то 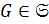 .
.
Теорема 1.2.1 (Свойства нормальных подгрупп).
Пусть 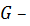 группа, тогда справедливы следующие утверждения:
группа, тогда справедливы следующие утверждения:
1) если 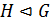 ,
, 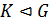 , то
, то 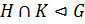 и
и 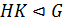 , то есть пересечение нормальных подгрупп есть нормальная подгруппа и произведение нормальных подгрупп есть нормальная подгруппа;
, то есть пересечение нормальных подгрупп есть нормальная подгруппа и произведение нормальных подгрупп есть нормальная подгруппа;
2) если 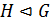 ,
, 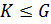 , то
, то 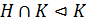 , то есть пересечение нормальной подгруппы с произвольной нормальна в произвольной;
, то есть пересечение нормальной подгруппы с произвольной нормальна в произвольной;
3) если 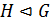 ,
, 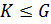 и
и 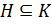 , то
, то 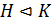 , то есть нормальная подгруппа является нормальной в любой подгруппе ее содержащей.
, то есть нормальная подгруппа является нормальной в любой подгруппе ее содержащей.
Теорема 1.2.2. Минимальная нормальная подгруппа группы является характеристически простой группой.
Теорема 1.2.3. Характеристически простая группа является прямым произведением изоморфных простых групп.
Следствие 1.2.1. В нильпотентной группе все максимальные подгруппы нормальны и имеют простые индексы.
Теорема 1.2.4 (Миллер). 1. Факторгруппа  /
/ 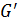 абелева;
абелева;
2. если 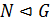 и
и 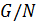 абелева, то
абелева, то 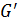 ≤
≤ 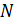 ;
;
3. если 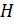 ≤
≤  ,
, 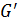 ≤
≤ 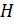 , то
, то 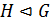 и
и 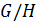 абелева.
абелева.
Теорема 1.2.5. 1. Если 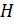 — максимальная нормальная подгруппа неединичной группы
— максимальная нормальная подгруппа неединичной группы  , то факторгруппа
, то факторгруппа 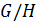 является простой группой.
является простой группой.
2. Если 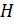 — нормальная подгруппа группы
— нормальная подгруппа группы  и факторгруппа
и факторгруппа 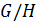 простая, то H — максимальная нормальная подгруппа группы
простая, то H — максимальная нормальная подгруппа группы  .
.
Теорема 1.2.6. Абелева простая группа, является циклической группой простого порядка. Обратно, каждая группа простого порядка будет простой абелевой группой.
Теорема 1.2.7 (Первая теорема Силова ). Пусть 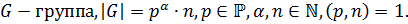 Тогда в
Тогда в  существуют силовские -подгруппы.
существуют силовские -подгруппы.
