Полнота булевых функций

Система функций 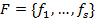называется полной (функционально полной), если её замыкание совпадает с множеством булевых функций, т.е. любую булеву функцию можно представить в виде суперпозиции функций системы .

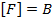
Теорема: (о полноте двух систем)
Пусть даны две системы булевых функций 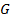и ; система 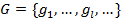и 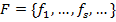о которых известно, что:

1. Система 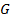– полная

2. Каждую функцию системы 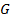можно представить, как суперпозицию функций системы , т.е.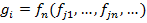

Тогда система является полной.

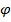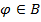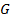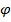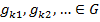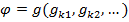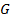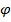Доказательство: рассмотрим произвольную булеву функцию , ; так как система полна, то функцию можно представить, как суперпозицию некоторых функций этой системы, то есть , но так как каждая функция из , в том числе и выбранные, представимы в виде суперпозиции функций , то функцию можно представить в следующем ви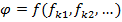де: , где 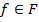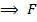– полная.
Теорема: (о функциональной полноте)
Для того, чтобы система булевых функций была полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из 5 замкнутых классов: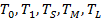
Доказательство: 1) Необходимость: мы предполагаем, что – полная. Предположим противное: пусть содержится в некоторых из перечисленных классов. 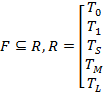Каждый из классов является замкнутым 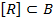(содержится, но не совпадает). Так как, система полна, то 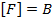. С одной стороны, из 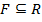, то 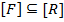, С другой стороны 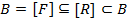. Множество строго включено в себя 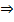получено противоречие.
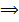
не может содержаться целиком ни в одном из замкнутых классов.

2) Достаточность: целиком не содержится ни в одном из пяти классов. Докажем, что - полная. Для этого из системы функций рассмотрим не более пяти булевых функций: 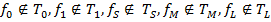. Формируем новую систему 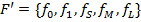. Возьмём класс 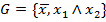. Нам известно, что этот класс полный. Покажем, что функции класса 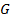можно представить в виде суперпозиции функций системы 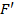(а следовательно и функций системы ). Возьмём 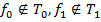. Построим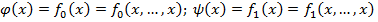

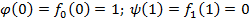
Доопределим 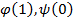(рассмотрим все возможные варианты):

1.
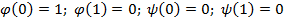
тогда 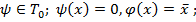из функци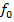й и 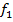получаем 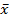и 0;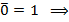

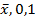
2.
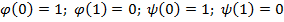
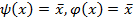; возьмём 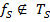, по лемме о несамодвойственной функции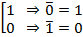

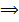
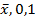
3.
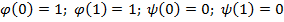
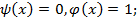возьмём 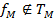, по лемме о немонотонной получаем функцию одной переменной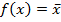

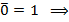
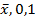
4.
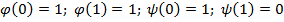
тогда 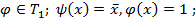из функци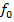й и 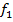получаем 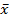и 1; .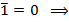

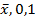Возьмём нелинейную функцию 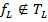. По лемме о нелинейной функции мы получаем нелинейную функцию двух переменных 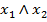. Таким образом функции класса 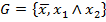можно получить из функций класса .
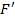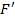⟹ - полный и система – полная
Теорема: (критерий Эмиля Поста)

Из всякой полной системы можно выделить полную подсистему 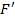, , 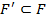содержащую не более четырёх функций.
Доказательство: согласно теореме о функциональной полноте, из полной системы можно выделить полную 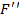, содержащую не более пяти функций, однако: рассмотрим 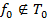. Эта функция в точке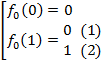
В случае 1 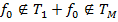, в случае 2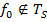

Пусть 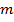некоторый класс булевых функций. Система булевых функций 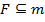называется полной в 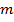, если её замыкание 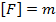при этом 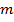считается замкнутым классом.

Система булевых функций из замкнутого класса 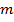называется базисом в 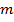, если она является полной в 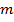, а любая её подсистема полной в 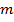не является.

Теорема1: каждый замкнутый класс булевых функций имеет конечный базис.

Теорема 2: мощность множества замкнутых классов булевых функций является счётной.

Предикаты.