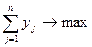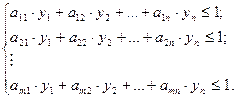Игра двух лиц с нулевой суммой

В игре двух лиц с нулевой суммой (такую игру называют также антагонистической) принимают участие два игрока: игрок 1 и игрок 2. В распоряжении каждого игрока имеется множество стратегий. Под стратегией понимают совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.

Пусть 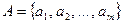— множество стратегий игрока 1, 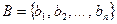— множество стратегий игрока 2. Элементы множества A — возможные стратегии (действия) игрока 1, элементы множества B — стратегии игрока 2.

При условии, что множества A и B — конечны, их элементы образуют платежную матрицу. И такая игра называется матричной.

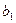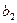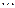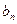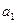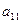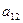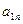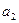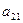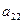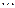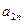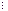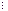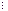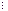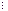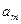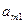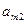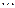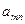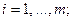
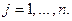
В игре двух лиц с нулевой суммой, как и в любой другой стратегической игре, исход зависит от поведения обоих игроков, которое основывается на так называемых правилах игры. Допустим, что согласно правилам игры, игрок 1 может выбрать произвольную строку матрицы и, следовательно, может выбрать одно из чисел 1, 2, ..., m. Аналогично, игрок 2 имеет возможность выбора произвольного столбца матрицы выигрышей и, следовательно, одного из чисел 1, 2, ..., n. Исход (результат) игры и, следовательно, сумму, которую игрок 2 должен уплатить игроку 1, определяет элемент матрицы выигрышей, находящийся на пересечении строки, выбранной игроком 1, и столбца, выбранного игроком 2. Существенно, что ни один из партнеров не знает, какую стратегию применит его противник. Таким образом, имеет место ситуация полной неопределенности, при которой теория вероятности не может помочь игрокам в выборе решения. Рассмотрим процесс принятия решений обеими сторонами более детально, предполагая, что игроки действуют рационально.

Если игрок 1 не знает, как поступит его противник, то, действуя наиболее целесообразно, не желая рисковать и считая, что противник также будет действовать целесообразно, он выберет такую стратегию, которая гарантирует ему наибольший из наименьших выигрышей при любой стратегии противника. Принято говорить, что при таком образе действий игрок 1 руководствуется принципом максиминного выигрыша. Этот выигрыш определяется следующей формулой:

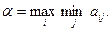
Величина 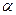называется нижней ценой игры, максиминным выигрышем, или сокращенно максимином.

В свою очередь игрок 2, действуя рационально, выберет такую стратегию, которая гарантирует ему наименьший из возможных проигрышей при любых действиях противника. Принято говорить, игрок 2 руководствуется принципом минимаксного проигрыша. Этот проигрыш определяется следующей формулой:

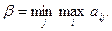
Величина 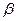называется верхней ценой игры или минимаксом. Принцип осторожности, который определяет выбор партнерами стратегий, соответствующих максиминному выигрышу или минимаксному проигрышу, часто называют принципом минимакса, а стратегии, вытекающие из этого принципа, — минимаксными стратегиями. Доказывается, что всегда 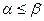, чем и объясняются названия «нижняя цена» и «верхняя цена».

Ситуация, когда 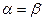, называется седловой точкой. При этом результат стратегической игры двух лиц с нулевой суммой можно определить, не приступая к фактической игре: вполне реален сценарий, когда партнеры, взглянув на матрицу, рассчитываются, пожимают друг другу руки и расходятся. Очевидно, что исход такой игры не изменится, если она будет повторена многократно, поскольку ни одному из игроков невыгодно отклоняться от своих минимаксных стратегий.

В случае, когда 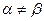, т.е. седловой точки нет, решение в чистых стратегиях отсутствует, используются смешанные стратегии и задается их вероятность.

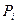— вероятности стратегий для первого игрока;

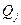— вероятности стратегий для второго игрока;

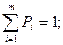
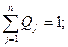
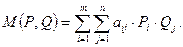
Цена игры равна математическому ожиданию от наиболее вероятных стратегий игроков:

;

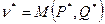Причем,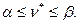

Максимизируется выигрыш первого 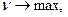а второй игрок стремится минимизировать свой проигрыш.

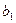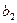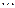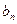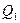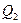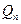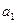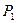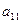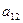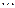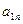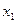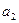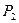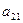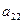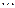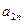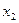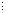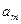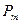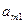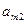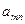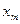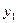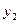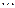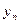Для первого игрока:

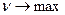
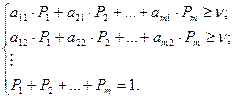
Поделим систему уравнений на 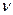и введем замену .

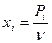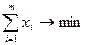
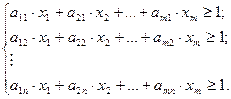
Для второго игрока:

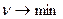
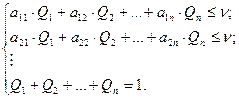
Поделим систему уравнений на 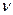и введем замену .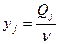