Алгоритм выполнения индивидуального задания №1

I. Простейшая статистическая обработка:

1) Упорядочить вариационный ряд (т.е. записать все значения вариант в порядке возрастания) (таблица 2).

2) Найти размах: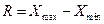

3) Подобрать количество разрядов (интервалов):

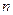, где -объём выборки (количество разрядов должно быть целым числом).

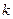4) Построить интервальную таблицу частот. Для этого находят длину интервала (если не делится нацело на , то можно слегка расширить диапазон значений случайной величины) и границы интервалов – точки , где . Затем подсчитывают частоты - количество значений случайной величины (вариант), попавших на каждый интервал.

В таблицу 3 заносят границы интервалов среднее значение вариант на каждом интервале , частоты 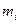и относительные частоты (частности) (столбцы 1-4).

II. Вычисления точечных оценок:

1)Вычислить выборочное среднее - оценку для математического ожидания.

2) Вычислить выборочную дисперсию - оценку для дисперсии.

3) Вычислить стандартное отклонение - оценку для среднего квадратичного отклонения.

III. Построение доверительного интервала дляa:

1) зная доверительную вероятность (надёжность) 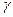, найти по таблице значений функции Лапласа (см. Приложение 1) соответствующее значениеt, для которого .

2) Вычислить предельную ошибку , где s- стандартное отклонение , n- объем выборки.

3) Записать доверительный интервал для математического ожидания

IV. Построение гистограммы:

Гистограмма – это столбиковая диаграмма, служащая для графического представления распределения частот. Площади столбцов пропорциональны частотам (или относительным частотам).

Для построения гистограммы относительных частот вычисляют высоты столбцов гистограммы (удобно добавить их в таблицу 3- столбец 5), на оси абсцисс отмечают тоски и над каждым интервалом строят прямоугольник высотой . В результате получается ступенчатая фигура, верхний контур которой приблизительно соответствует графику плотности распределения исследуемой случайной величины (рис.1)

V. Аппроксимация гистограммы нормальным законом распределения:

1) Составить таблицу значений теоретического нормального закона с параметрами

Для удобства расчетов можно:

а) найти значения ;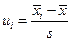

б) по таблицу найти (см. Приложение 2);

в) вычислить 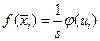(таблица 3 ).

2) Построить график теоретической кривой. На рисунке 3.1 отметить точки с координатами и соединить их плавной кривой.

3) Сделать вывод о согласованности статического распределения (гистограммы) с теоретическим нормальным законом распределения , проанализировав полученный рисунок.

VI.Проверка согласованности статического и теоретического распределения:

1) Вычислить статистику ,

где функция Лапласа.

2) Определить число степеней свободы r=k-3.

3) Анализ результатов. Выбрав уровень значимости 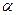( например, 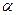=0,05), в таблице критических точек распределения 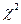(Приложение 3), найти .

Если , то можно принять гипотезу о нормальном распределение, т.е полученный теоретический закон хорошо аппроксимирует статическое распределение.

Если , то гипотеза о выборе теоретического закона отвергается, т.е полученный закон не согласуется с экспериментальными данными.