Численное решение рассмотренных задач

Задача растяжения панели. Приведем расчет вариантов напряженно-деформированного состояния при растяжении панели, рассмотренных в разд. 3.5, и проанализируем полученные результаты. Как видно, эти варианты позволят определить необходимое количество выбираемых функций перемещений и и необходимый уровень их ортогонализации.

Решение и весь анализ проведем на примере растяжения панели силой , приложенной посередине поперечной балки на свободном краю. Примем следующие расчетные параметры панели: длина панели м, высота панели м, площади поперечных сечений контурных балок для продольных стержней и поперечных балок равны см², момент инерции поперечных балок см ⁴, модуль упругости балки стержня принят ГПа. Для пластины панели берем композитную однонаправленную ленту со следующими характеристиками: модуль упругости вдоль направления волокон ГПа, поперек – ГПа, модуль сдвига ГПа, коэффициент Пуассона , углы укладки и толщины слоев мм; мм. Для расчета рассматриваемой задачи примем следующие функции. Функция отвечает продольному перемещению поперечного сечения панели как жесткого целого при растяжении. Остальные функции учитывают депланацию сечения от силы с учетом геометрических условий точечного закрепления по координате y и отвечают смыслу задачи. Первичные функции и для задачи растяжения можно выбирать как в тригонометрическом, так и полиномиальном видах: ; или ; и т.д., учитывающих депланацию при растяжении, и или , а также ; или ; ; и т.д., учитывающих поперечное обжатие панели в соответствии с выбранными функциями растяжения. Эти функции удовлетворяют геометрическим граничным условиям, отвечают условиям и виду приложенных нагрузок и характеру возможных перемещений, т.е. функция учитывает, что перемещения постоянны в сечении и в пластине, и в продольных подкрепляющих элементах. Функция учитывает линейное перемещение в сечении панели по координате , т.е. деформацию сечения по координате при растяжении. Остальные начальные функции учитывают, что в точках при перемещения в точках крепления и .

Были решены пять вариантов одной и той же задачи, но с разным количеством функций и и различным подходом к ортогонализации этих функций. Выпишем разрешающую систему уравнений, содержащую по три заданных функции, на основе которой и проведем исследование точности и сходимости решения:

(3.34)

Как показало исследование, увеличение числа членов ряда не всегда повышает точность расчета. Выражения для коэффициентов уравнений (3.34) приведены в (3.12).

С учетом вида первоначально выбранных функций, а также того, что и , в задаче растяжения равны нулю коэффициенты , а между остальными коэффициентами существует связь ; ; ; ; ; ; ; ; ; ; ; ; ; .

В первом варианте решения были заданы три функции: ; ; . Проведя ортогонализацию функций и , получим три разрешающих уравнения

;

;

.

Аналитическое решение этой системы дано в разд. 3.5, а графическое представление дано на рис. 3.7, где показаны изменения перемещений при , а на рис. 3.8 показаны изменения напряжений , по координате при . Распределение силы вдоль подкрепляющего элемента показано на рис. 3.9 (где приведены решения для всех иллюстрируемых вариантов). Если судить по величине этой силы в заделке для рассмотренного варианта, то видно, что распределение слишком неточно и ошибка составляет %. Это не приемлемо при определении напряженно-деформированного состояния панели.

Решение с четырьмя первообразными функциями ; ; и дается в четырех вариантах. Рассмотрим их последовательно.

В первом варианте проводится полная ортогонализация между выбранными функциями и их производными таким образом, что обращаются в нуль все коэффициенты с индексами 12 и 21. Этот вариант рассмотрен в разд. 3.1.5. Выпишем еще раз разрешающие две подсистемы уравнений

(3.35)

Решение этой системы приведено в разд. 3.5. Однако константы можно определить только для первых двух функций, а для двух других функций константы решения равны нулю, и поэтому решение является менее точным,

Рис.3.7. Перемещения u и v по

длине панели

Рис.3.8. Изменение напряжений и

по координате при

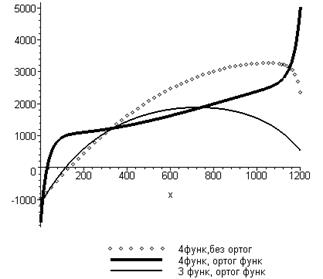
Рис. 3.9. Изменение силы в продольном направлении

чем предыдущее и полная ортогонализация разрешающей системы с разделением на подсистемы недопустима.

Теперь приведем вариант, когда между двумя системами остается связующий коэффициент . Для этого в решении отбросим функцию , а разрешаемая система примет вид

(3.36)

Проинтегрировав, как обычно, первое уравнение, решаем его совместно с остальными тремя.

Для сравнения результатов представленных систем рассмотрим также решение полной системы с ортогонализацией только первоначально выбранных функций перемещений и между собой:

(3.37)

И, наконец, рассмотрим решение полной связанной системы без ортогонализации функций и между собой:

(3.38)

Решение систем (3.37) и (3.38) можно проводить или непосредственным интегрированием уравнений, или после интегрирования первого уравнения. Сравним решения представленных вариантов. На рис. 3.10, 3.11 даны распределения напряжений по длине панели для вариантов решения

Рис.3.10. Распределение напряжений по длине (3.37)

Рис. 3.11. Распределение напряжений по длине (3.38)

(3.37) и (3.38), соответственно, а изменение силы вдоль продольного пояса показано на рис.3.9. Из этого сравнения видно, что в случае выбора варианта с ортогонализацией четырех функций точность расчета составляет %, тогда как без ортогонализации решение дает ошибочный результат. Два других варианта, представленных системами (3.35) и (3.36), дают неверный результат и не могут быть рекомендованы к решению. Как показал непосредственный расчет, увеличение количества членов ряда более четырех в ряду выбранных функций не приводит к уточнению решения рассматриваемой задачи. Если рассмотреть решение для варианта с тремя функциями ( ; ; ) и двумя функциями ( и , то его точность существенно падает. Дальнейшее увеличение последовательности задаваемых функций не повышает точности решения. Поэтому рассмотренное решение с четырьмя функциями и их последующей ортогонализацией дает наиболее точный результат. Конечно, характер растягивающих сил должен учитываться видом выбираемых по координате функций.

Изгибаемая панель. Теперь рассмотрим поперечный изгиб, когда приложенные силы имеют кососимметричное расположение, т.е. верхняя и нижняя кромки поперечной балки при нагружены силами (см. рис. 3.5). Для решения задачи примем следующие выражения для выбираемых функций по координате . В первом случае рассмотрим решение с тремя первообразными функциями : ; ; и тремя функциями : ; ; . Проведя ортогонализацию функций, разрешающую систему запишем с учетом вида выбранных функций и значений коэффициентов в виде

(3.39)

Здесь учтено, что ; ; в результате ортогональности функций в этих выражениях, а между коэффициентами существует связь ; ; ; ; ; ; .

Проинтегрировав четвертое уравнение системы (3.39) и учтя условие на границе , оно принимает вид с учетом связи между коэффициентами

. (3.40)

Учитывая связь между балочными функциями уравнения (3.40) и первым уравнением системы (3.39), его можно переписать в виде

или, проинтегрировав один раз и удовлетворив статическое граничное условие , в виде

. (3.41)

Тогда разрешающая система будет содержать второе, третье, пятое уравнения системы (3.39) и уравнения (3.40) и (3.41).

Для сравнения была рассмотрена и решена вторая система, в решении которой участвовали четыре заданные функции ; ; ; . В этом случае разрешающая система с учетом преобразований предыдущего варианта примет вид

(3.42)

На рис. 3.12 приведено распределение напряжений , вдоль оси для первого варианта, а на рис. 3.13 – для второго варианта. На рис. 3.14 и 3.15 приведены сравнительные варианты для перемещений и и вдоль координаты .

Как видно из проведенных расчетов, краевое приложение сил при растяжении и изгибе всегда приводит к концентрации напряжений в обшивке в этих точках. Для напряжения максимальные напряжения возникают на краю , так как закрепление верхнего и нижнего краев панели препятствует свободной деформации в поперечном направлении и могут превышать продольные напряжения в раза.

Рис. 3.12. Распределение напряжений по длине

при (первый вариант)

Рис.3.13. Распределение напряжений по длине

при (второй вариант)

Рис. 3.14. Сравнение расчетных вариантов для перемещений

Рис. 3.15. Сравнение расчетных вариантов для силы