Методические указания к выполнению задания.

1.2.1.Особенности записии решений уравнений по законам Кирхгофа при синусоидальном токе.

При составлении уравнений по законам Кирхгофа в интегродифферен-циальной форме следует учесть , что уравнения составляются для мгновенных значений напряжений и токов и что падение напряжения на активном сопротивле- нии u _R= i· R, на индуктивной катушке u _L= L di / dt , на конденсаторе u _C=1 / С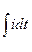

При анализе гармонических процессов в цепях составляются уравнения в комплексной форме. При этом необходимо учесть, что падение напряжения на резисторе Ú _R=Í∙R, на индуктивности Ú _L = j x _L ∙Í , на конденсаторе Ú _С= - j x _C ∙ Í .

Для получения численного результата необходимо проводить расчеты с комплекс- ными числами.

1.2.2. Определение токов в ветвях. Для цепи, содержащей три ветви, целесообразно определить полное комплексное сопротивление. Отношение эдс

источника к этому сопротивлению позволяет определить ток в ветви, в которой расположен источник эдс. Далее, находят напряже- ние на параллельном участке и затем, разделив это напряжение на сопротивления двух других ветвей, находят соответствующие токи. Правильность решения проверяют по первому закону Кирхгофа.

1.2.3.Баланс мощностей.

При составлении баланса мощностей следует рассчитать мощность,

развиваемую источником эдс, и приравнять ее сумме мощностей всех потребителей.

Ś _ИСТ = Σ Ś _ПОТР.

Полная мощность в комплексной форме определяется как

Ś=Σ Ú·Î = P + (-) j Q = Σ Z·Í∙Î , где

P- активная мощность,

Q- реактивная мощность,

Î - комплексное сопряженное значение к –того тока,

Z – полное комплексное сопротивление к-той ветви.

1.2.4.Построение векторной диаграммы токов и топографической диаграммы

напряжений.

Следует помнить, что вектор падения напряжения на резисторе Ú _R совпадает по фазе с током, на индуктивной катушке Ú _L опережает вектор тока на 90 градусов,

а на конденсаторе Ú _С отстает от тока на угол 90 градусов.

1.2.5. Построение кривых мгновенных значений.

В результате расчетов значения тока и напряжения получены в комплексной форме, необходимо записать эти величины в функции времени.

u _АВ= U _{АВ m} sin ( ω t + ψ _UАВ ) , для чего находится амплитудное

значение напряжения и начальная фаза

U _{АВ m} = U _АВ · 1,41

U _АВ =√ Re ² + Im² ψ _UАВ= arctq Im / Re

1.2.6. Определение показаний ваттметра.

Ваттметр измеряет активную мощность, поэтому при определении показаний ваттметра необходимо взять действительную часть от произведения комплекса соот- ветствующего напряжения на величину сопряженного комплекса тока.

P= Re ( Ú _AB ∙ Î ) , где

Ú _AB – комплекс напряжения между точками A и B , к которым подключена

обмотка напряжения ваттметра,

Î- сопряженный комплекс тока, протекающего по токовой обмотке ваттметра.

Пример выполнения задания

Исходные данные для расчета:

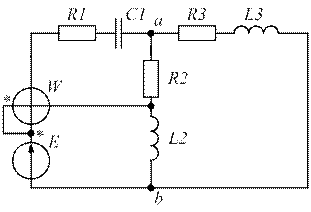
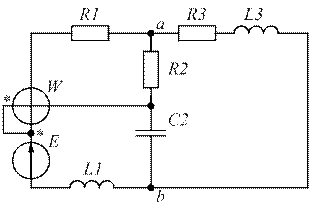
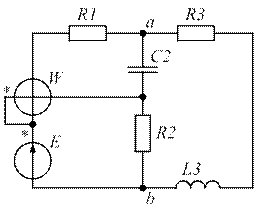
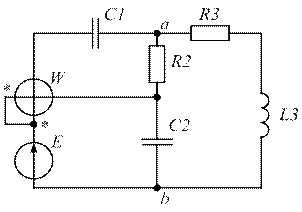
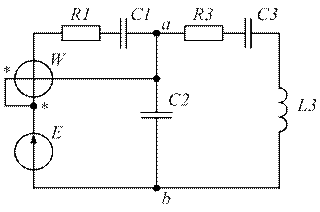
Схема электрической цепи представлена на рис. 1.

Параметры элементов схемы: Е= 220 В , f= 50 Гц, С ₁ = 825 мкФ, С₂ = 250 мкФ,

L ₁= 25 мГн , L ₂ =30 мГн , L₃ = 20 мГн , r ₁= 8,18 Ом , r ₂= 10 Ом , r ₃= 20 Ом .

1.3.1. Составление уравнений по законам Кирхгофа.

Количество уравнений по 1-му закону равно числу узлов, уменьшенному на единицу ( 2-1=1).

Количество уравнений по 2-му закону равно числу ветвей, уменьшенному на

количество уравнений, составленных по 1-му закону ( 3-1=2).

Система уравнений в интегро-дифференциальной форме:

i ₁ = i ₂ + i ₃

e = r ₁ i ₁ + 1/C_{1 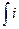1} dt + u _C1 ( 0) + L ₁ di ₁/dt + L ₃ di ₃/dt + r₃ i ₃

0= r ₂ i ₂ + L ₂ di ₂/dt + 1/C_{2 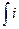2} dt+ u _C2 ( 0) - L ₃ di₃ /dt - r₃ i ₃

Система уравнений в комплексной форме:

Í₁ =Í₂ + Í₃

É = ( r₁ + j x _L1 – j x _C1 ) Í ₁ + ( r₃ + j x _L3 ) Í ₃

0 = ( r₂ + j x _L2 – j x _C2 ) Í ₂ - ( r₃ + j x _L3 ) Í ₃

1.3.2. Расчет токов в цепи в комплексной форме.

Сопротивления ветвей:

Z ₁ = ( r₁ + j x _L1 – j x _C1 ) = 8,18 – j 3,86 + j 7,85= 8,18 + j 3,99 ( Ом)

j x _L1 = j 2 п f L ₁ = j 2 ∙3,14·50·25∙10 ^-3 =j 7, 85 ( Ом)

– j x _C1 = -j 1 / 2п f C ₁ = - j 1/ 2· 3,14· 50 · 825· 10 ^{– 6} = - j 3,86 ( Ом )

Z ₂ = r₂ + j x _L2 – j x _C2 = 10+ j 2 п f L ₂ - j 1 / 2п f C ₂ =

= 10 + j 2 ∙3,14· 30· 50∙10 ^-3 - j 1/ 2· 3,14· 50 · 250· 10 ^{– 6} = 10 – j 3,32 ( Ом )

Z ₃ = r₃ + j x _L3 = 20 + j 2 п f L ₃= 20 + j 2 ∙3,14· 50· 20∙10 ^-3 = 20 + j 6, 28 ( Ом)

Нахождение полного комплексного сопротивления:

(10 – j 3,32) (20 + j 6, 28)

Z = Z ₁ + Z ₂ Z ₃ / Z ₂ +Z ₃ = 8,18 + j 3,99 + ------------------------------------ =

(10 – j 3,32) + (20 + j 6, 28)

= 15,45 + j 3,17 ( Ом)

Ток в неразветвленной части цепи:

Í ₁ = É / Z ₁ = 220 / 15,45 + j 3,17 = 13,66 - j 2,78 ( А )

Напряжение разветвленной части цепи:

Ú _АВ = É - Z ₁ Í ₁ = 220 – ( 8,18 + j 3,99 ) ( 13,66 - j 2,78 ) = 97,08- j 31,76 ( В )

Токи в ветвях:

Í ₂ = Ú _АВ / Z ₂ =( 97,08-j 31,76) / (10 – j 3,32) = ( 9,69 + j 0,05 ) ( А)

Í ₃ = Ú _АВ / Z ₃ =( 97,08-j 31,76) / ( 20 + j 6, 28 ) = ( 3,97 – j 2,83) ( А)

Проверка по первому закону Кирхгофа:

Í ₁ = Í ₂ + Í ₃ = ( 9,69 + j 0,05 ) + (3,97 – 2,83) = 13,66 – j 2,78 ( А)

1.3.3.Баланс активных и реактивных мощностей.

Комплексная мощность источника:

Ś = É_i ∙ Î_i = 220 ∙ (13,66 + j 2,78) = 3005,2+j 616,6 ( ВА)

Активная мощность источника Р _i = 3005, 2 Вт

Реактивная мощность источника Q _i = 611, 6 Вар

Комплексные мощности приемников:

Ś _{1 ПР} = Z₁ ∙ Í ₁ Î₁ = ( 8,18 + j 3,99 ) ( 13,66 - j 2,78 ) ( 13,66 + j 2,78 ) =

= 1590,8 + j 775,56 ( ВА)

Ś _{2 ПР} = Z₂ ∙ Í ₂ Î₂ = (10 – j 3,32) ( 9,69 + j 0,05 ) ( 9,69 - j 0,05 ) =

= 939,01 - j 312,6 ( ВА)

Ś _{3 ПР} = Z₃ ∙ Í ₃ Î₃ = ( 20 + j 6, 28 ) (3,97 – j 2,83) (3,97 +j 2,83) =

= 475,28 + j 148,65 ( ВА)

Комплексная мощность всех приемников:

Ś _ПР = Ś _{1 ПР} + Ś _{2 ПР} + Ś _{3 ПР} =1590,8 + j 775,56 + 939,01 - j 312,6 +

+ 475,28 + j 148,65 = 3005,09 + j 611, 61 ( ВА)

Активная мощность потребителей Р = 3005, 09 Вт

Реактивная мощность потребителей Q = 611, 61 Вар

1.3.4.Построение векторной диаграммы токов и топографической диаграммы.

На комплексной плоскости наносят вектора токов в ветвях ( комплексные

значения), причем вектор тока Í ₁ должен быть равен сумме векторов Í ₂ и Í ₃

( рис. 1.1.1 ).

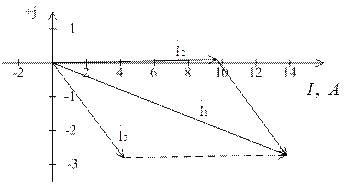
Для построения топографической диаграммы потенциал одного узла прини мают за нуль

φ _В =0

Потенциал следующей точки φ _К возрастает на величину падения напряжения

– j x _C2·Í₂

φ _К = φ _В + ( – j x _C2·Í₂ )= 0 + ( - j 12,7) ( 9,69 +j 0,05) = 0,64 – j 123,1 B

φ _M = φ _K + ( r₂·Í₂ ) = 0,64 – j 123,1+ ( 9,69+j 0,05) 10 = 97,5- j 122,6 B

φ _A = φ _M + ( j x _L2·Í₂ ) = 97,5- j 122,6 + ( 9,69+j 0,05) ( j9,42) = 97,0 – j 31,3 B

φ _Q = φ _A + ( j x _L1·Í₁ ) = = 97,0 – j 31,3 + ( j 7,85)( 13,66-j 2,78) = 118,8+j 75,9

φ _N = φ _Q + ( – j x _C1·Í₁ ) = 118,8+j 75,9 + (- j 3,86) ( 13,66-j 2,78) = 108,1+j 23 B

φ _D = φ _N + ( r₁ ·Í₁ ) =108,1+j 23 + 8,18 ( 13,66-j 2,78) = 220- j 0,1 B

φ _В = φ _D - É = 220 - j 0,1 - 220 =0

( рис. 1.1.2.)

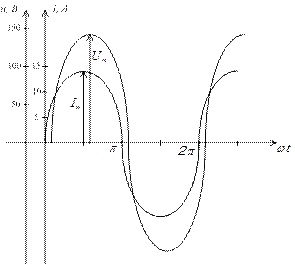
1.3.5.Построение кривых мгновенных значений.

В результате расчетов значения тока и напряжения получены в комплексной

форме

Í ₂ = ( 9,69 + j 0,05 ) ( А)

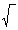Модуль тока I₂ = 9,69² + 0,05² = 9,7 (А)

Амплитудное значение I _m = 1,41∙I₂ = 13, 68 ( А)

Начальная фаза тока ψ _i= arc tq 0,05 / 9,69 = 0,3 град.

Мгновенное значение тока

i₂ = I _m sin ( ω t + ψ _i2 ) = 13, 68 sin (ω t + 0,3°) (A)

Ú _АВ = 97,08 - j 31,76 ( В )

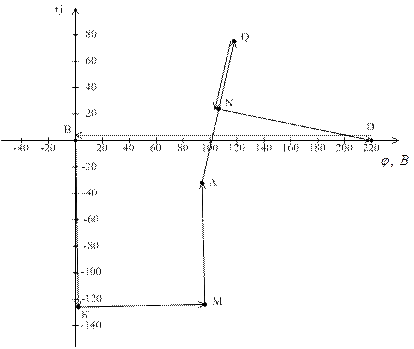
Модуль напряжения U _AB = 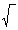97,08² + 31,76² = 102, 1 (В)

Амплитудное значение U _{АВ m} = 1,41∙ U _AB=1,41· 102,1= 144 ( В)

Начальная фаза напряжения ψ _U = arc tq (- 31,76) / 97,08= - 18,1 град.

Мгновенное значение напряжения u _АВ= U _{АВ m} sin ( ω t + ψ _UАВ ) =

= 144 sin ( ω t - 18 °) (В)

( рис.1.1.3.)

1.3.6. Определение показаний ваттметра.

P_w = Re (Í_w·Ú_w )=Re ( - j X _C2 ∙Í₂∙Î₂) = Re { (- j 1/ 2· 3,14· 50 · 250· 10 ^{– 6}) ·

·( 9,69 + j 0,05 ) ( 9,69 - j 0,05 ) } = Re ( 6,17- 6,17+ j 1196,2 + j 0,03) = 0

Ú_w =( - j X _C2 ∙Í₂ ) Í_w = Î₂

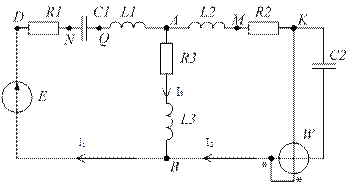	Векторная диаграмма токов
Рис. 1.	Рис.1.1.1.

Топографическая диаграмма	Кривые мгновенных значений
Рис.1.1.2.	Рис.1.1.3.

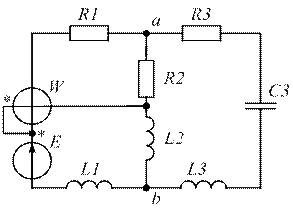Рис. 1.1.	Рис. 1.2.
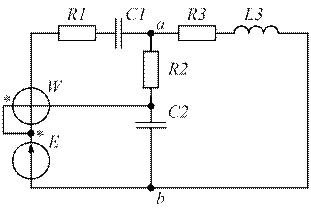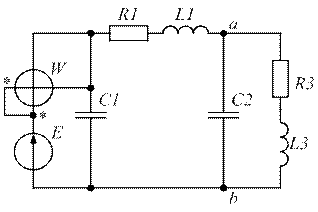
Рис. 1.3.	Рис. 1.4.
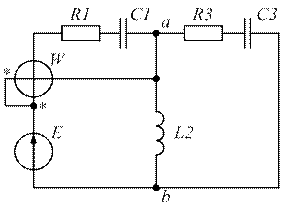Рис. 1.5.	Рис. 1.6.
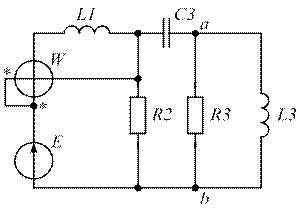Рис. 1.7.	Рис. 1.8.

Рис. 1.9.	Рис. 1.10.
Рис. 1.11.	Рис. 1.12.
Рис. 1.13.	Рис. 1.14.
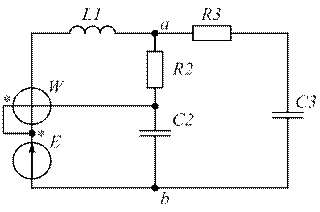Рис. 1.15.	Рис. 1.16.

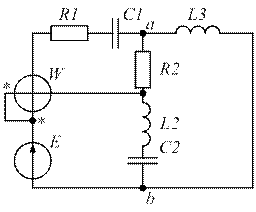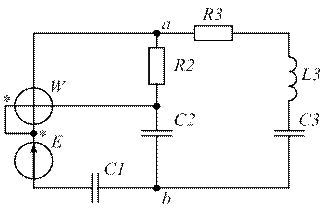Рис. 1.17.	Рис. 1.18.
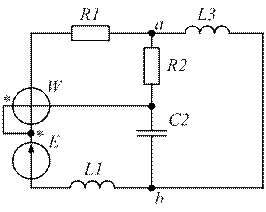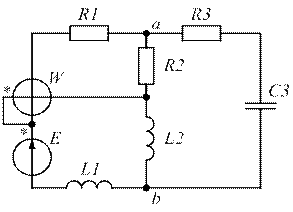Рис. 1.19.	Рис. 1.20.
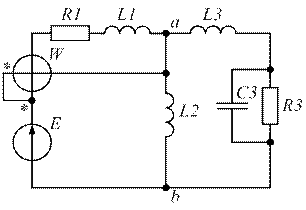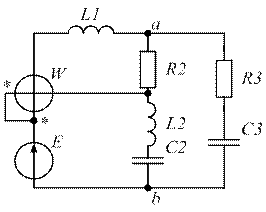Рис. 1.21.	Рис. 1.22.
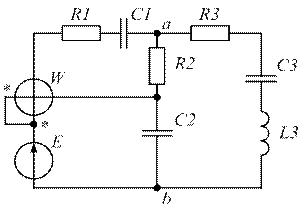Рис. 1.23.	Рис. 1.24.

Рис. 1.25.	Рис. 1.26.
Рис. 1.27.	Рис. 1.28.
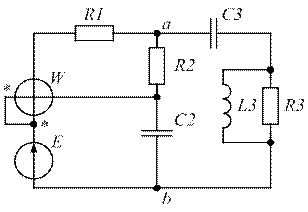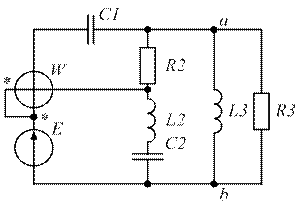Рис. 1.29.	Рис. 1.30.
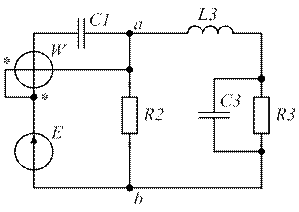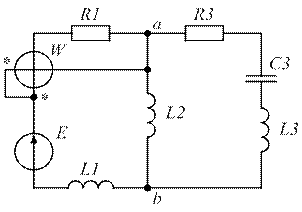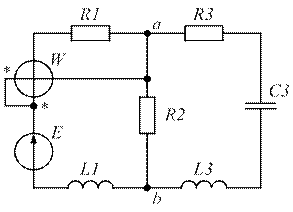
Рис. 1.31.	Рис. 1.32.

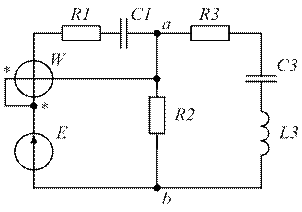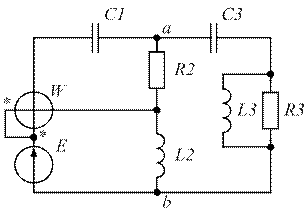Рис. 1.33.	Рис. 1.34.
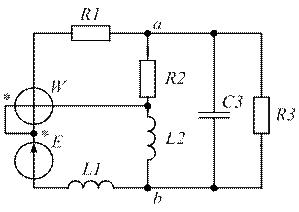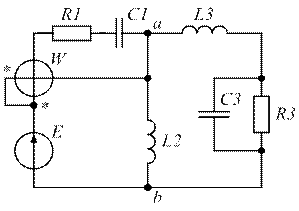Рис. 1.35.	Рис. 1.36.
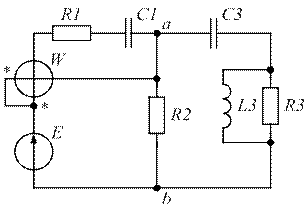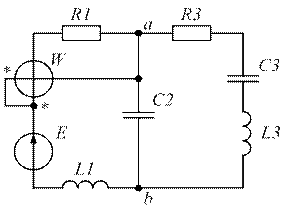Рис. 1.37.	Рис. 1.38.
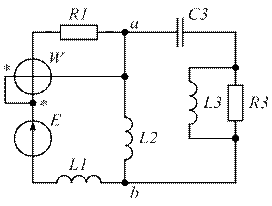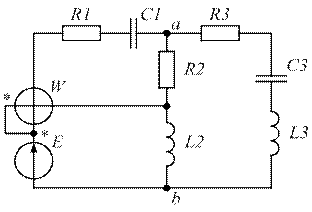Рис. 1.39.	Рис. 1.40.

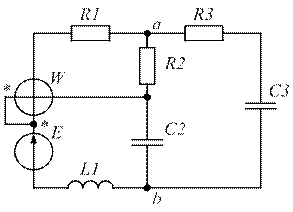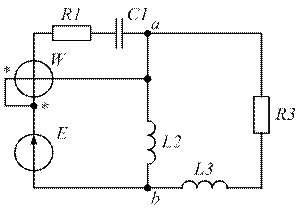Рис. 1.41.	Рис. 1.42.
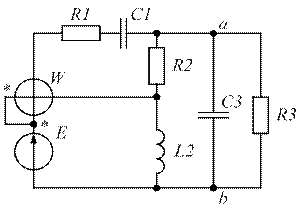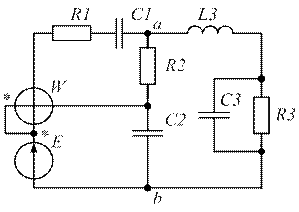Рис. 1.43.	Рис. 1.44.
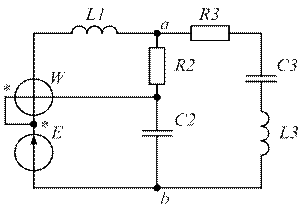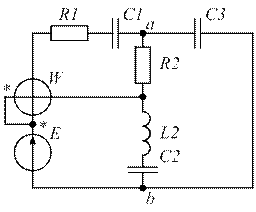Рис. 1.45.	Рис. 1.46.
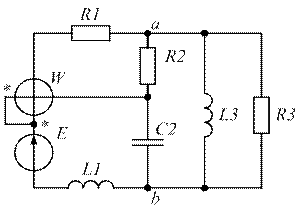Рис. 1.47.	Рис. 1.48.

Рис.1.49. Рис. 1.50.

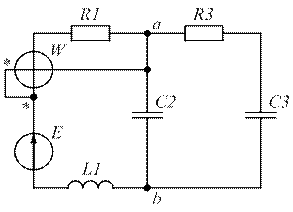
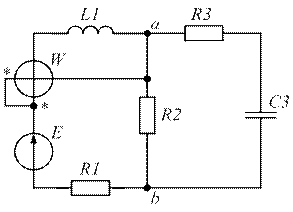
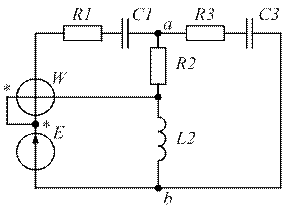
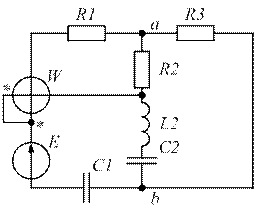
Варианты задания №1. Таблица 1

№ ва-рианта	№ схем	Е, В	f, Гц	С1, мкФ	С2, мкФ	С3, мкФ	L1, мГн	L2, мГн	L3, мГн	R1, Ом	R2, Ом	R3, Ом
					-	-	-	31,8	63,7
				-	-		25,5	22,3	15,9
						-	-	-	25,5
				-		-	15,9	-	47,7
					-		-	22,3	-		-
						-	15,9	-	31,8		-
				-	-		47,7	-	31,8	-
				-		-	-	-	25,5
				-		-	47,7	-	-
				-		-	31,8	-	22,3		-
					-		-	18,6	-
				-			53,1	-	-		-
				-	-		13,3	-	-
					-		-	21,2	-
						-	-	13,3	-
				-			13,3	-	-	-
						-	-	26,5	21,2			-
							-	-	26,5	-
				-		-	26,5	-	18,6			-
				-	-		26,5	18,6	-
				-	-		47,7	31,8	47,7		-
				-			47,7	31,8	-	-
							-	-	31,8
						-	-	-	26,5	-
				-	-	-	31,8	47,7	-
						-	-	-	13,3		-
					-		21,2	13,3	-		-
				-	-		53,1	-	53,1
				-			-	-	53,1
						-	-	26,5	26,5	-
					-		-	-	13,3	-
				-	-		13,3	18,6	53,1		-
					-		-	-	13,3

№ ва-риант	№ схемы	Е, В	f, Гц	С1, мкФ	С2, мкФ	С3, мкФ	L1, мГн	L2, мГн	L3, мГн	R1, Ом	R2, Ом	R3, Ом
					-		-	21,2	13,3	-
				-	-		26,5	21,2	-
					-		-	31,8	15,9		-
					-		-	-	15,9
				-			15,9	-	47,7		-
				-	-		31,8	25,5	47,7		-
					-		-	25,5	47,7
				-			15,9	-	-
					-	-	-	22,3	25,5		-
					-		-	22,3	-
							-	-	31,8
				-			31,8	-	22,3	-
							-	63,7	-			-
				-		-	25,5	-	22,3
							-	-	25,5		-
						-	-	25,5	31,8
				-			15,9	-	15,9