Раздел 2. Основные численные методы.

Тема 2.1. Численное интегрирование.

Метод прямоугольников

Из курса дифференциальной математики известно, что любая элементарная функция имеет производную. Однако, операция интегрирования не всегда осуществима. Хотя теоретически, интеграл существует 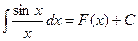. Но функцию F(x) нельзя выразить как конечную комбинацию элементарных функций. Такие интегралы-«неберущиеся», они вычисляются приближенно.

Пусть требуется найти 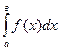, f(x)- непрерывная функция на отрезке (а;в)

По геометрическому смыслу определенного интеграла, он равен площади криволинейной трапеции, ограниченной графиком непрерывной функции, осями координат и прямыми х=а и х=в. Искомую площадь разобьем на части, для этого отрезок (а;в) разделим на n равные отрезки 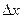, и рассмотрим каждую часть как прямоугольник, выразим его площадь. Затем суммируем полученные площади и получим приближенное значение площади криволинейной трапеции.

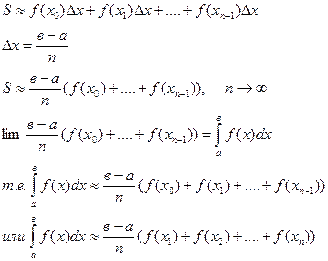
формула прямоугольников

Задача. Вычислить интеграл метолом прямоугольников. Оценить погрешность.

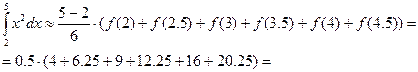
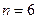
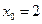
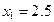
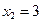
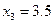
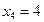
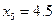
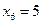
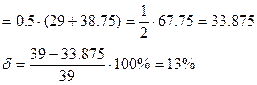
Метод трапеций

Найдем определенный интеграл, рассмотрев каждую составляющую часть площади криволинейной трапеции как прямоугольную трапецию. Выразим площадь каждой трапеции по формуле, известной из курса планиметрии, суммируем и получим приближенное значение площади криволинейной трапеции, а значит и приближенное значение определенного интеграла

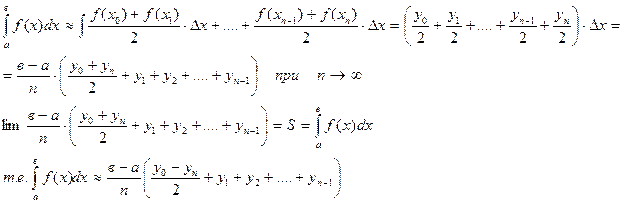
Задача. Найти приближенно 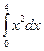по формуле трапеции. Оценить погрешность.

…..

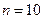
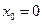
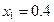
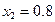
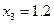
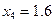
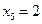
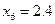
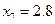
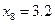
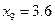
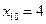
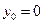
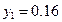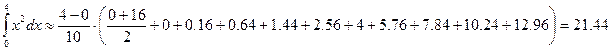
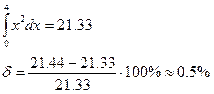
Тема 2.2. Численное дифференцирование

Пусть функция у=f(x) задана таблично, требуется найти производную функции f(x)

В этих случаях прибегают к приближенному дифференцированию. Возможно что непосредственное дифференцирование функции оказывается слишком сложным и тогда т можно воспользоваться приближенным дифференцированием

Искомую функцию заменяют полиномом Р(х) (алгебраическим многочленом), отвечающим определенным требованиям, совпадающем по значению в заданных точках х

Приближённое восстановление функции с помощью алгебраического многочлена называется интерполяцией функции f.

Полином, которым заменяют функцию f называют интерполяционным многочленом, точки х_i, i=0,1,2,3,…,n (в которых заданы значения функции) называются узлами интерполяции.

Пусть задана функция у=f(x) в равноотстоящих точках х_i, (i=0,1,2,3,…,n) отрезка [а;в], тогда функцию f заменяют интерполяционным полиномам Ньютона

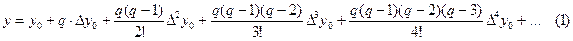
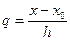, h=х_i+1-x_i – шаг интерполяции.

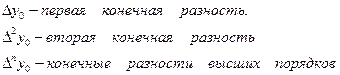
Если нужно вычислить значение производной в узлах x_i, то х=х₀ и тогда q=0

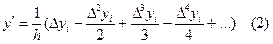
i=(0,1,2,3,…n)

Примр1: По табличным данным найти аналитическое выражение функции.

x
f(x)	10,4		20,8	24,8		30,4

Составляется таблица конечных разностей:

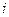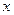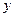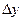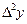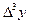		10,4	5,6	-0,8
			4,8	-0,8
		20,8		-0,8
		24,8	3,2	-0,8
			2,4
		30,4

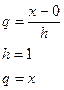
По формуле интерполяционного многочлена Ньютона получаем

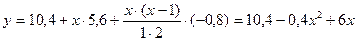
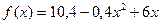
Пример 2. Функция задана таблично, найти аналитическое выражение её производной.

x
y

Таблица конечных разностей для заданной функции

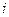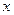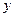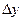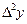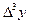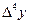Найдите значения производной в точках x₀, x₁, x₂, x₃, x_4……. по формуле (2), h=1

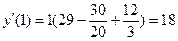
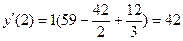
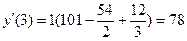
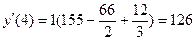
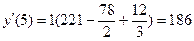
Составим таким же образом таблицу конечных разностей для функции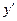

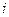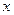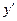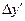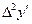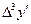По формуле (1)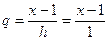

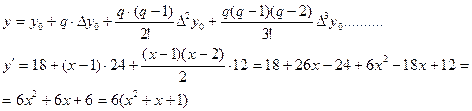
Таким образом, искомая производная