Непрерывность функции в точке
Задание №1.
1. Записать число 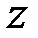 в алгебраической, тригонометрической и показательной формах, изобразив его на комплексной плоскости.
в алгебраической, тригонометрической и показательной формах, изобразив его на комплексной плоскости.
2. Вычислить 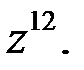
3. Вычислить 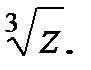
4. Составить квадратное уравнение, одним из корней которого является число 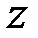 .
.
Задание №2.
Вычислить пределы.
Задание №3.
Подобрать параметры 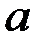 и
и 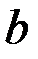 таким образом, чтобы функция
таким образом, чтобы функция 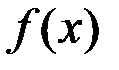 была непрерывна.
была непрерывна.
Задание №4.
Продифференцировать функции по переменной 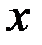 .
.
Задание №5.
Исследовать функцию с помощью производной и построить её график.
Вариант 1
Задание №1.1. 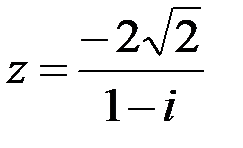 ; 2.
; 2. 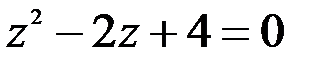
Задание №2. 1. 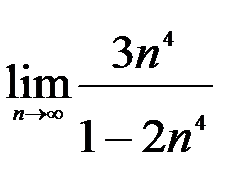 ; 2.
; 2. 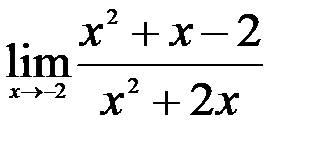 ; 3.
; 3. 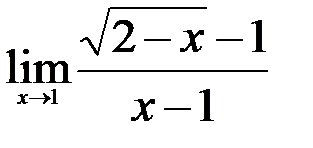 .
.
Задание №3.
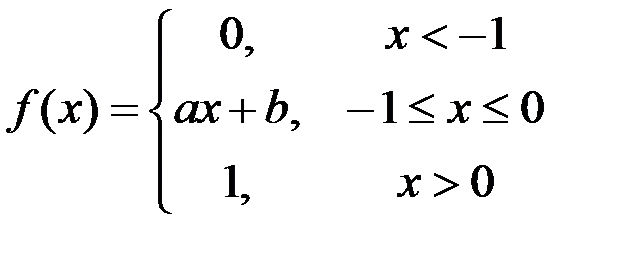 .
.
Задание №4.
1. 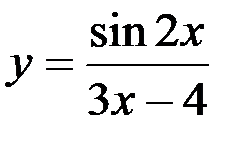 ; 2.
; 2. 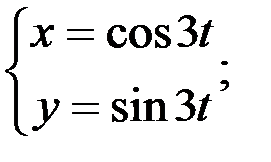 3.
3. 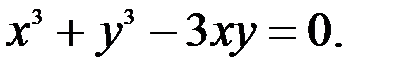
Задание №5. 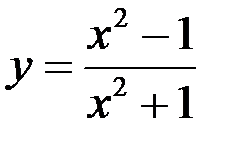 .
.
Вариант 2
Задание №1.1. 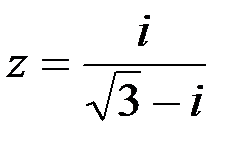 ; 2.
; 2. 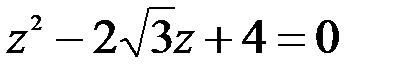 .
.
Задание №2. 1. 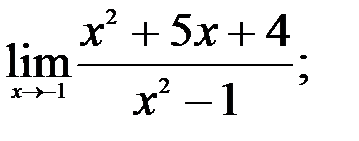 2.
2. 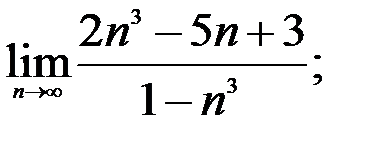 3.
3. 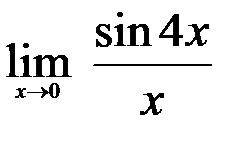 .
.
Задание №3.
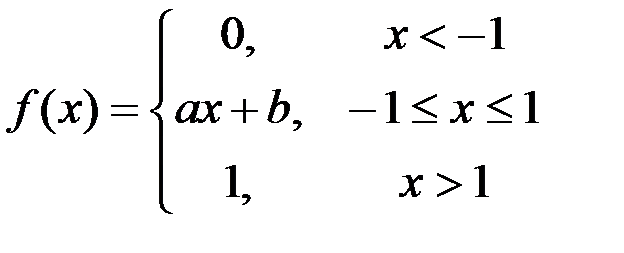 .
.
Задание №4.
1. 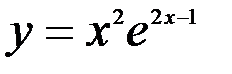 ; 2.
; 2. 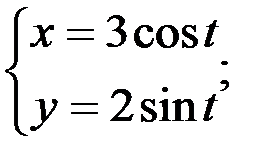 3.
3. 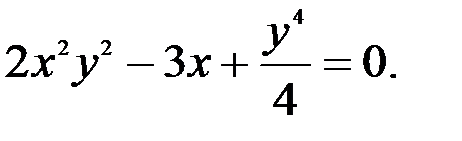
Задание №5. 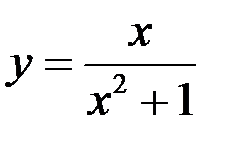 .
.
Вариант 3
Задание №1.1. 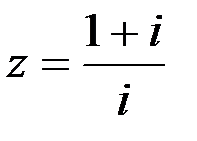 ; 2.
; 2. 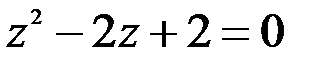 .
.
Задание №2. 1. 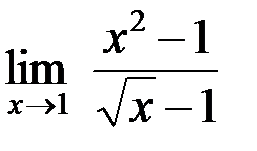 ; 2.
; 2. 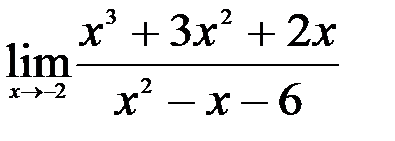 ; 3.
; 3. 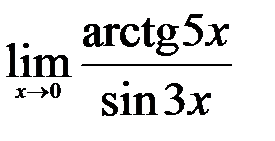 .
.
Задание №3.
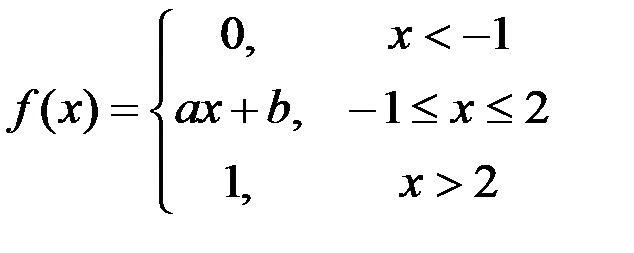 .
.
Задание №4.
1. 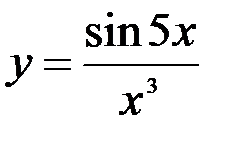 ; 2.
; 2. 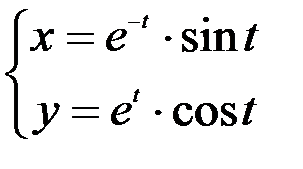 ; 3.
; 3. 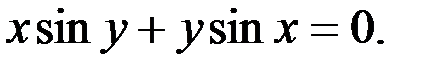
Задание №5. 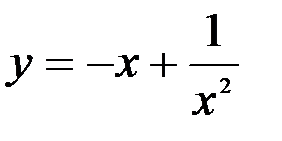 .
.
Вариант 4
Задание №1.1. 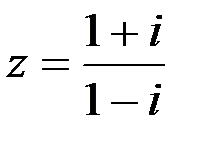 ; 2.
; 2. 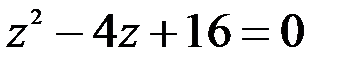 .
.
Задание №2. 1. 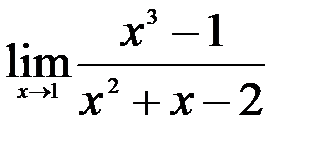 ; 2.
; 2. 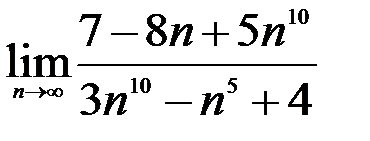 ; 3.
; 3. 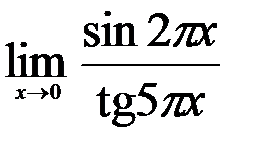 .
.
Задание №3.
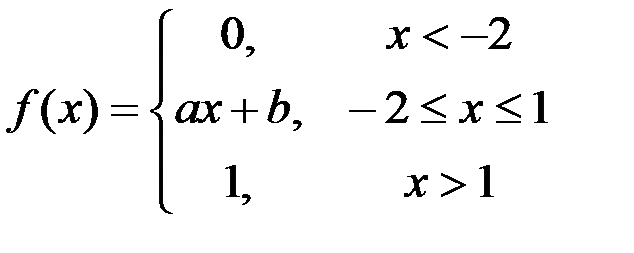 .
.
Задание №4.
1. 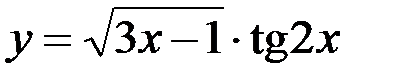 ; 2.
; 2. 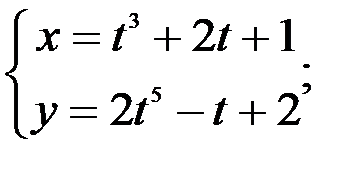 3.
3. 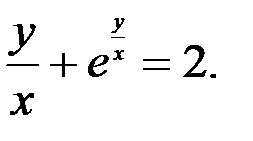
Задание №5. 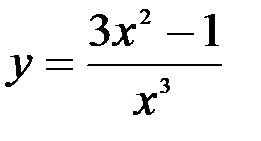 .
.
Вариант 5
Задание №1.1. 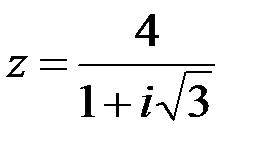 ; 2.
; 2. 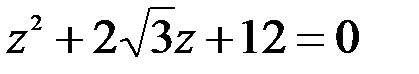 .
.
Задание №2.
1. 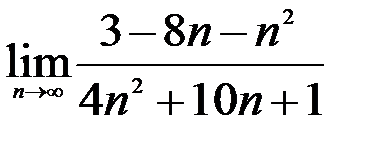 ; 2.
; 2. 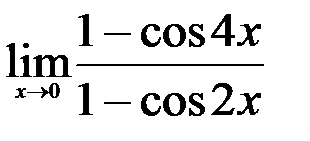 ; 3.
; 3. 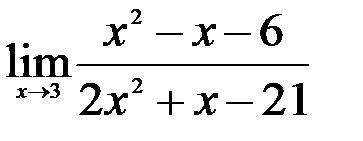 .
.
Задание №3.
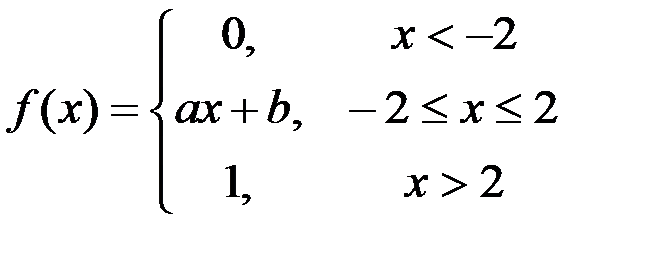 .
.
Задание №4.
1. 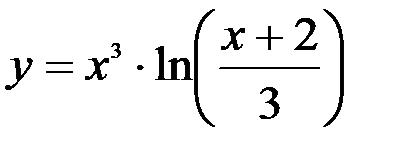 ; 2.
; 2. 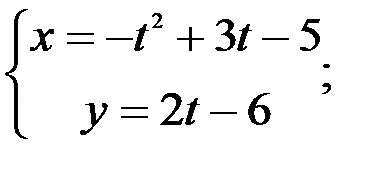 3
3 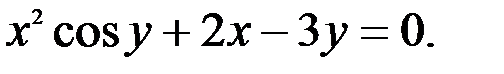
Задание №5. 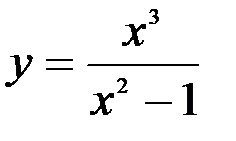 .
.
Вариант 6
Задание №1.1. 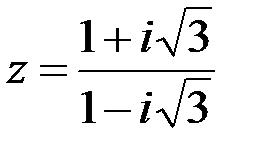 ; 2.
; 2. 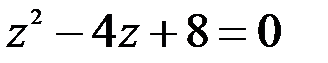 .
.
Задание №2. 1. 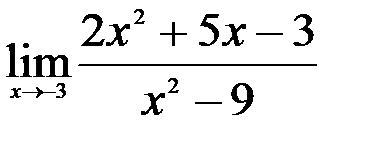 ; 2.
; 2. 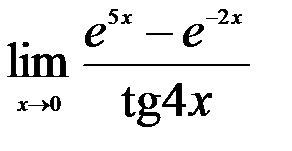 ; 3.
; 3. 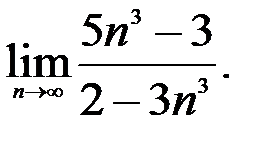
Задание №3.
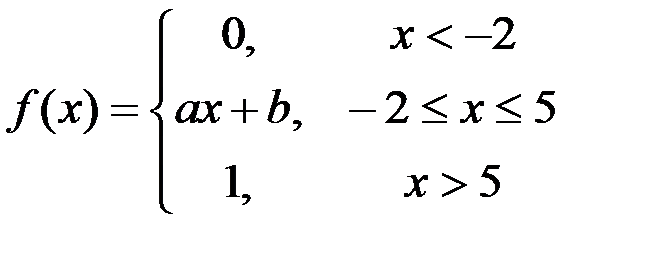 .
.
Задание №4.
1. 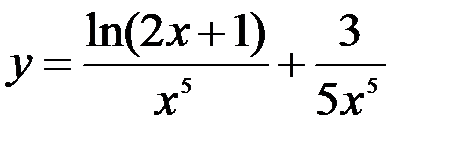 ; 2.
; 2. 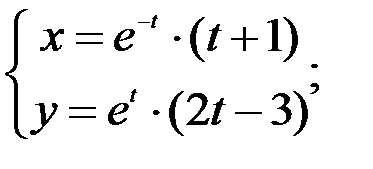 3.
3. 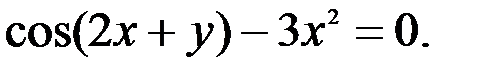
Задание №5. 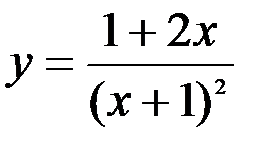 .
.
Вариант 7
Задание №1.1. 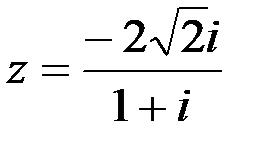 ; 2.
; 2. 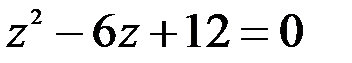 .
.
Задание №2. 1. 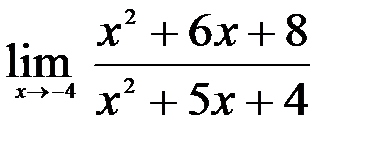 ; 2.
; 2. 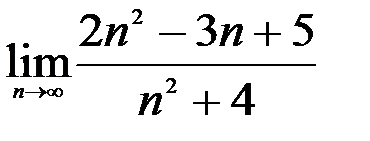 ; 3.
; 3. 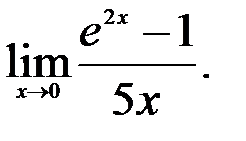
Задание №3.
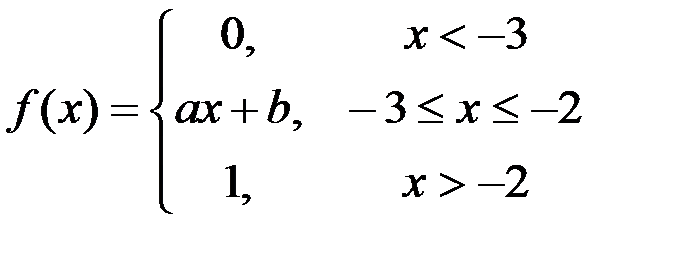 .
.
Задание №4.
1. 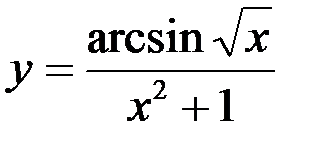 ; 2.
; 2. 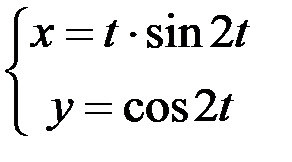 ; 3.
; 3. 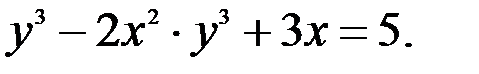
Задание №5. 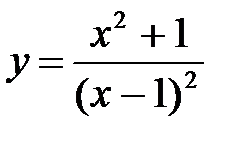 .
.
Вариант 8
Задание №1.1. 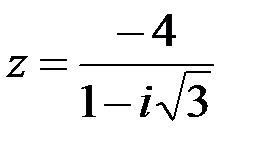 ; 2.
; 2. 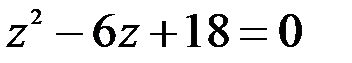 .
.
Задание №2. 1. 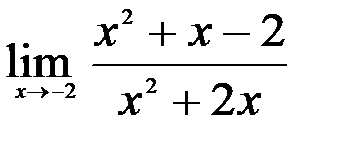 ; 2.
; 2. 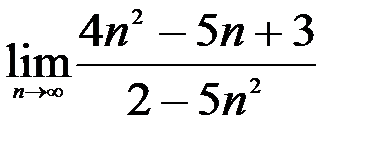 ; 3.
; 3. 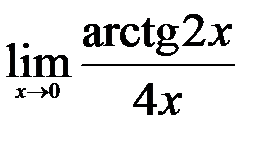 .
.
Задание №3.
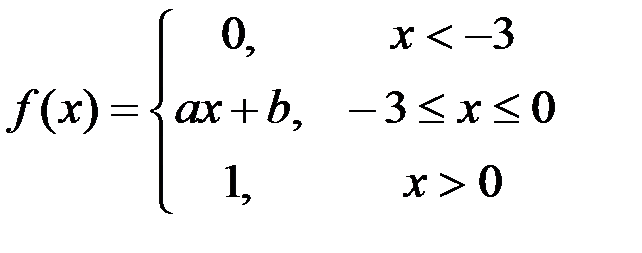 .
.
Задание №4.
1. 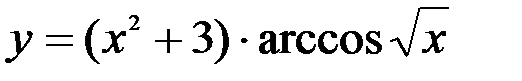 ; 2.
; 2. 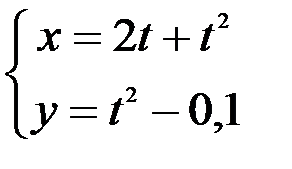 ; 3.
; 3. 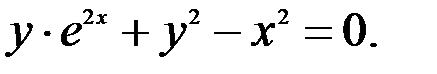
Задание №5. 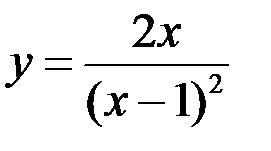 .
.
Вариант 9
Задание №1.1. 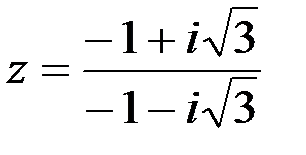 ; 2.
; 2. 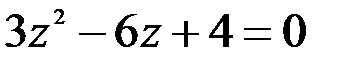 .
.
Задание №2.
1. 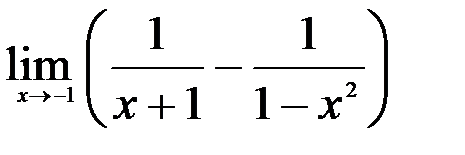 ; 2.
; 2. 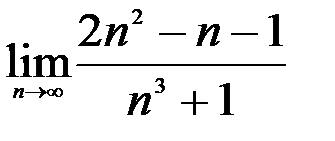 ; 3.
; 3. 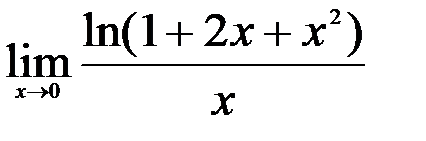 .
.
Задание №3.
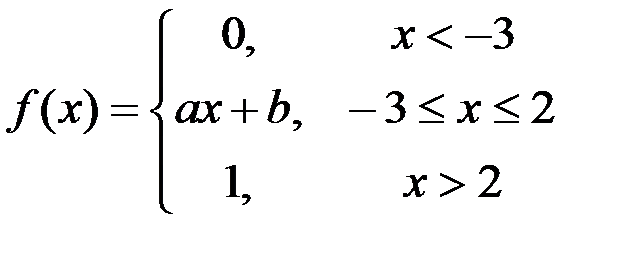 .
.
Задание №4.
1. 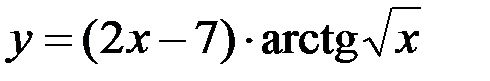 ; 2.
; 2. 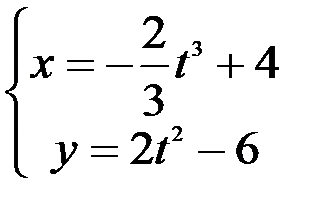 ; 3.
; 3. 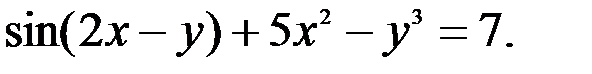
Задание №5. 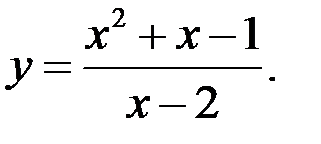
Вариант 10
Задание №1.1. 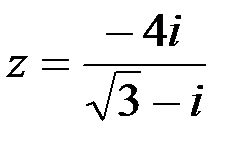 ; 2.
; 2. 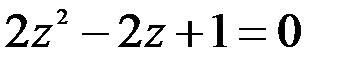 .
.
Задание №2.
1. 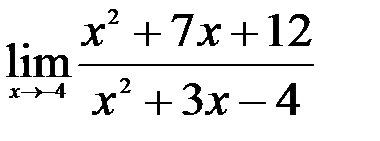 ; 2.
; 2. 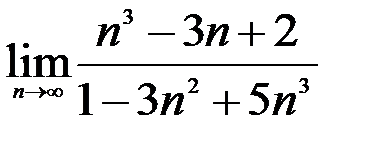 ; 3.
; 3. 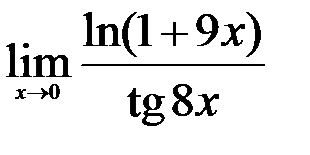 .
.
Задание №3.
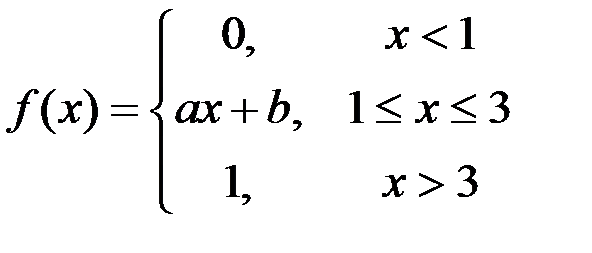 .
.
Задание №4.
1. 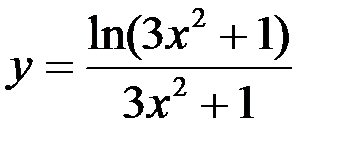 ; 2.
; 2. 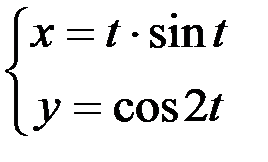 ; 3.
; 3. 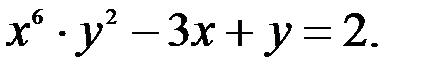
Задание №5. 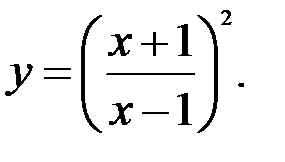
Вариант 11
Задание №1.1. 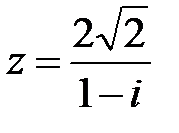 ; 2.
; 2. 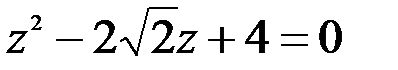 .
.
Задание №2. 1. 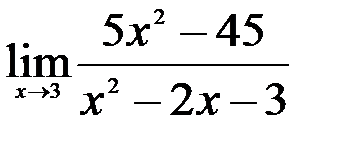 ; 2.
; 2.  ; 3.
; 3. 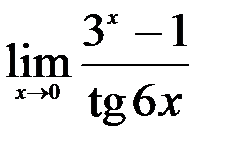 .
.
Задание №3.
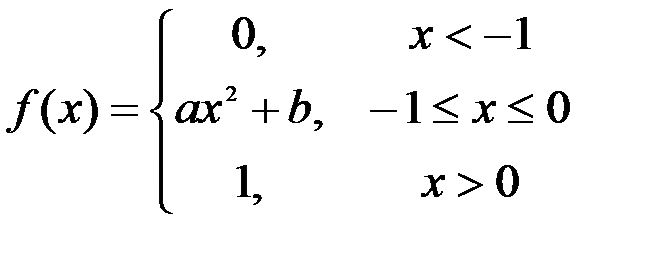 .
.
Задание №4.
1. 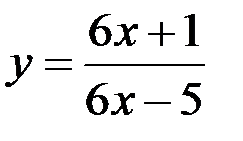 ; 2.
; 2. 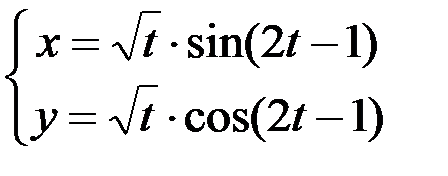 ; 3.
; 3. 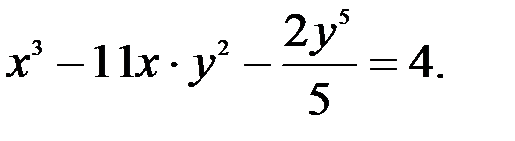
Задание №5. 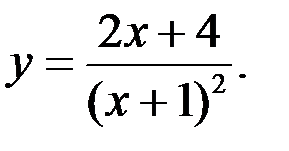
Вариант 12
Задание №1.1. 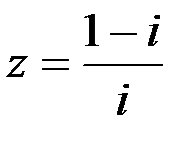 ; 2.
; 2. 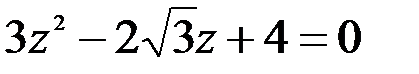
Задание №2. 1. 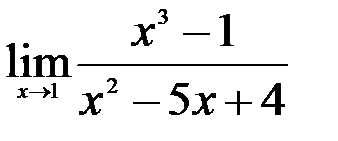 ; 2.
; 2. 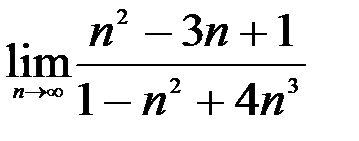 ; 3.
; 3. 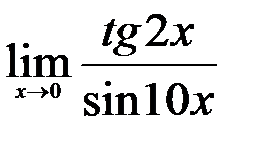 .
.
Задание №3.
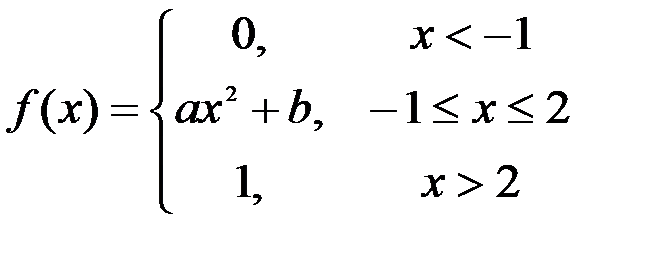 .
.
Задание №4.
1. 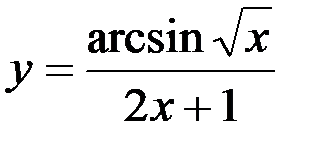 ; 2.
; 2. 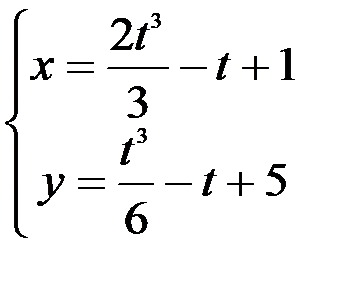 ; 3.
; 3. 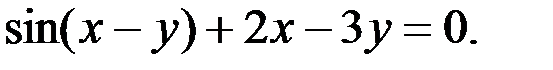
Задание №5. 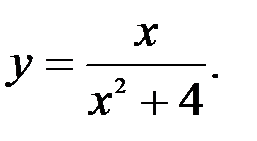
Вариант 13
Задание №1.1. 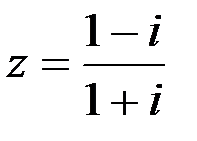 ; 2.
; 2. 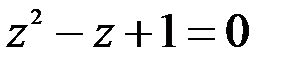 .
.
Задание №2.
1. 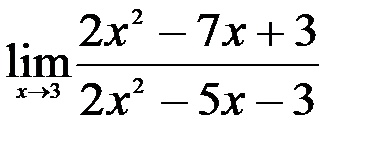 ; 2.
; 2. 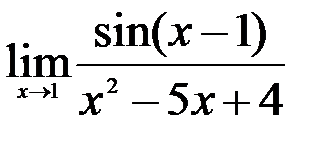 ; 3.
; 3. 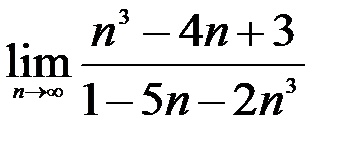 .
.
Задание №3.
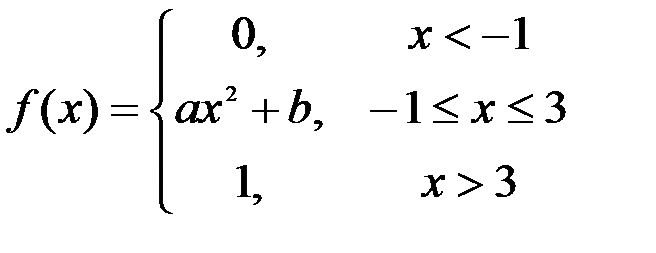 .
.
Задание №4.
1. 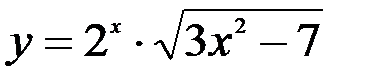 ; 2.
; 2. 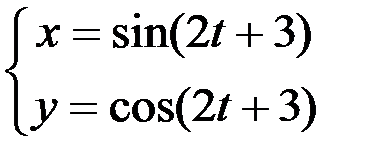 ; 3.
; 3. 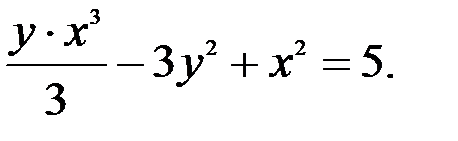
Задание №5. 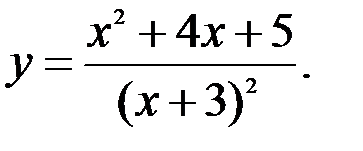
Вариант 14
Задание №1. 1. 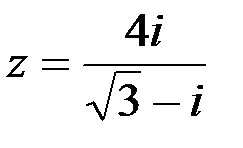 ; 2.
; 2. 
Задание №2.
1. 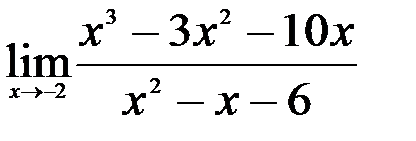 ; 2.
; 2. 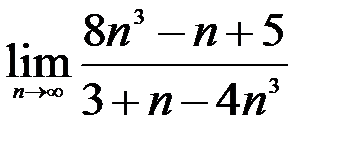 ; 3.
; 3. 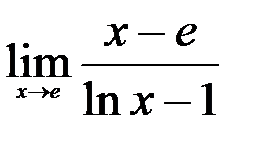 .
.
Задание №3.
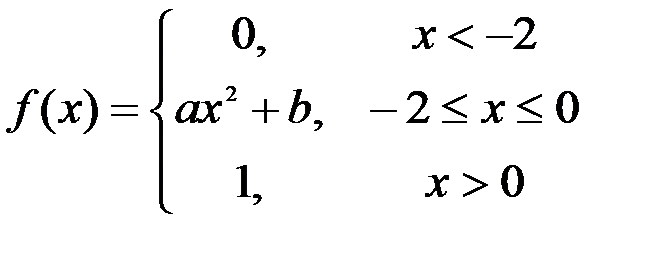 .
.
Задание №4.
1. 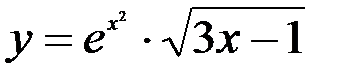 ; 2.
; 2. 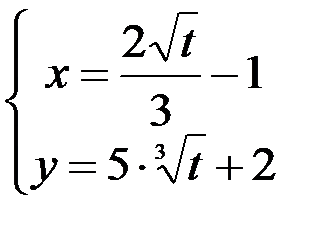 ; 3.
; 3. 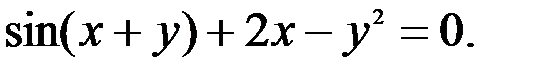
Задание №5. 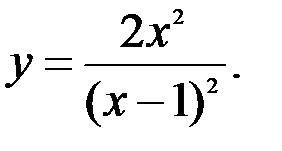
Вариант 15
Задание №1.1. 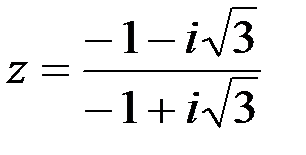 ; 2.
; 2. 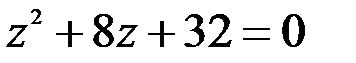 .
.
Задание №2.
1. 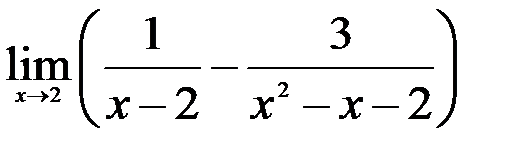 ; 2.
; 2. 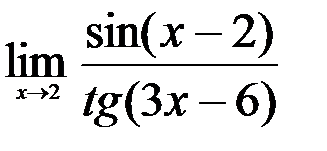 ; 3.
; 3. 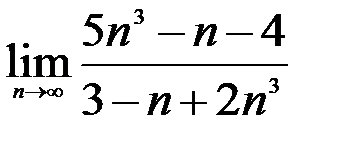 .
.
Задание №3.
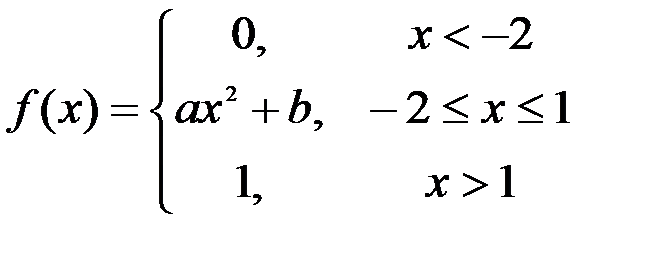 .
.
Задание №4.
1. 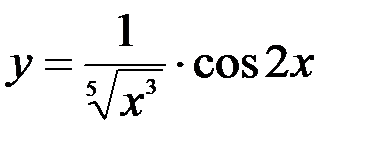 ; 2.
; 2. 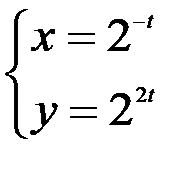 ; 3.
; 3. 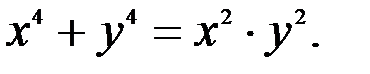
Задание №5. 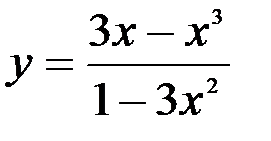 .
.
Вариант 16
Задание №1.1. 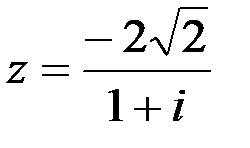 ; 2.
; 2. 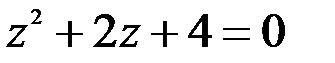 .
.
Задание №2. 1. 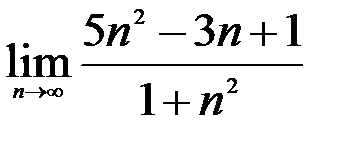 ; 2.
; 2. 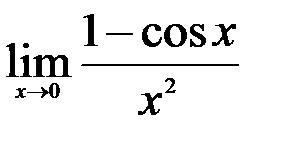 ; 3.
; 3. 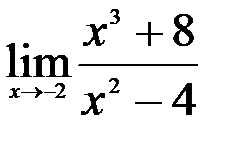 .
.
Задание №3.
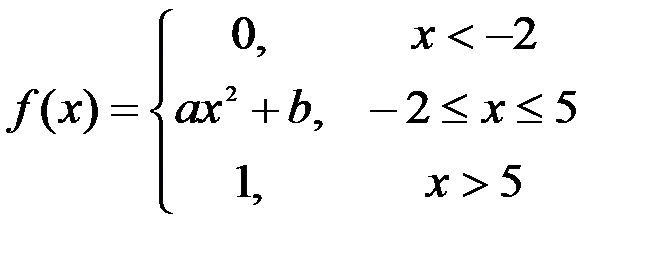 .
.
Задание №4.
1. 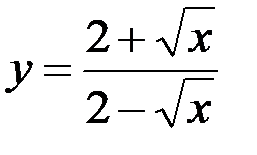 ; 2.
; 2. 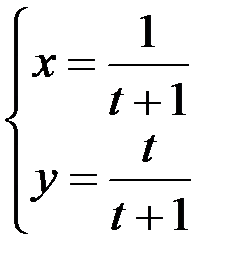 ; 3.
; 3. 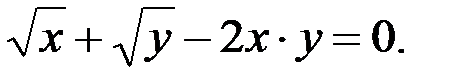
Задание №5. 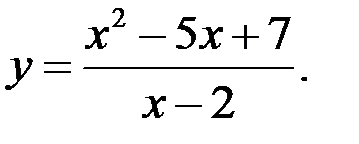
Вариант 17
Задание №1.1. 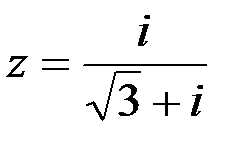 ; 2.
; 2. 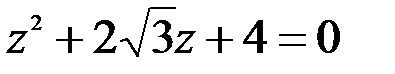 .
.
Задание №2. 1. 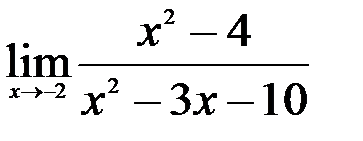 ; 2.
; 2. 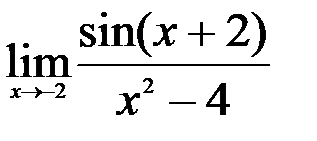 ; 3.
; 3. 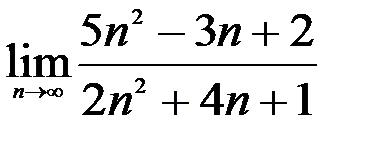 .
.
Задание №3.
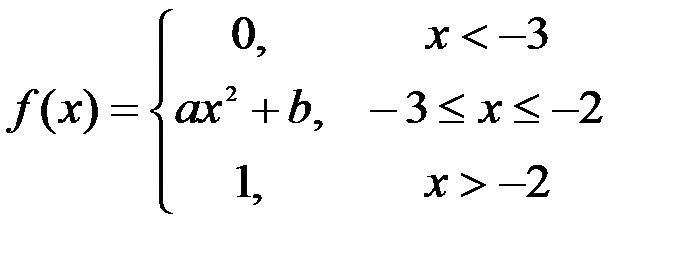 .
.
Задание №4.
1. 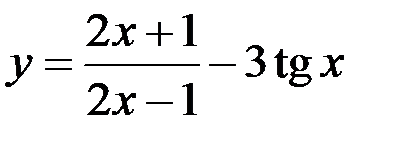 ; 2.
; 2. 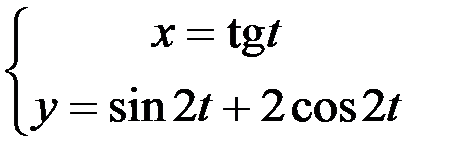 ;
;
3. 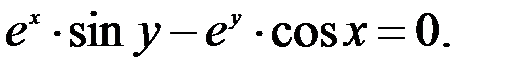
Задание №5. 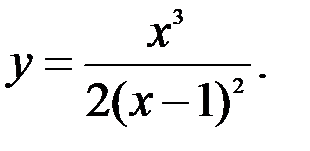
Вариант 18
Задание №1.1. 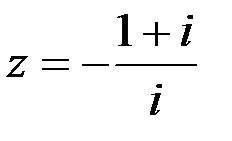 ; 2.
; 2. 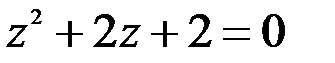 .
.
Задание №2.
1. 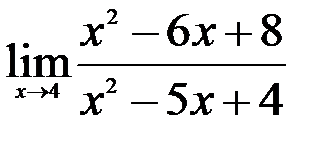 ; 2.
; 2. 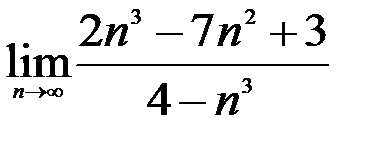 ; 3.
; 3. 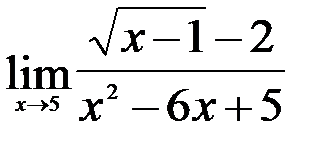 .
.
Задание №3.
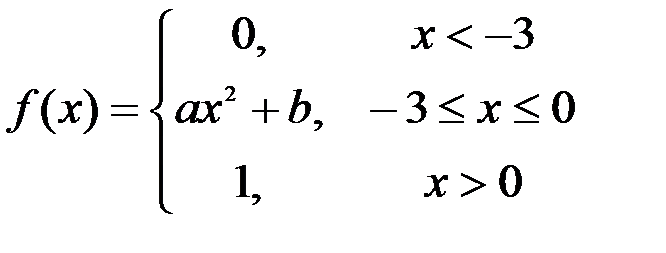 .
.
Задание №4.
1. 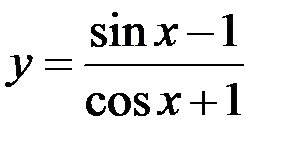 ; 2.
; 2. 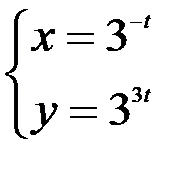 ; 3.
; 3. 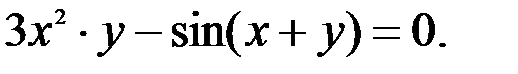
Задание №5. 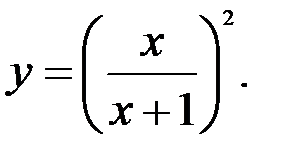
Вариант 19
Задание №1. 1. 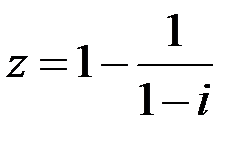 ; 2.
; 2. 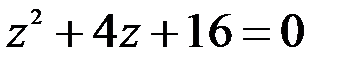 .
.
Задание №2.
1. 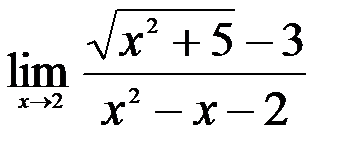 ; 2.
; 2. 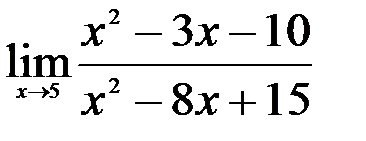 ; 3.
; 3. 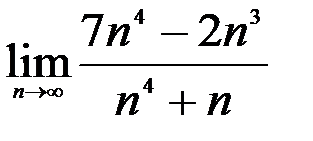 .
.
Задание №3.
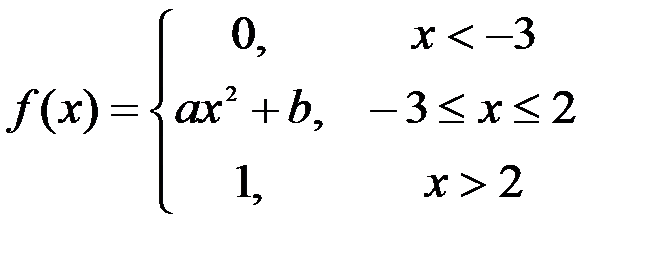 .
.
Задание №4.
1. 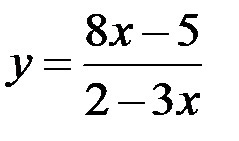 ; 2.
; 2. 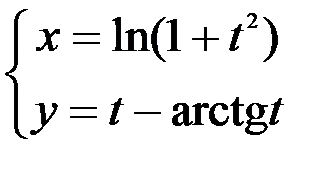 ; 3.
; 3. 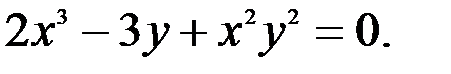
Задание №5. 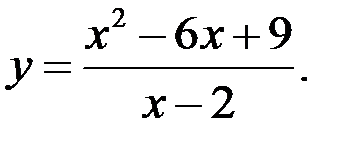
Вариант 20
Задание №1.1. 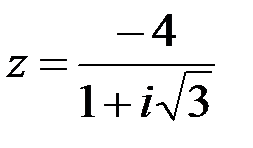 ; 2.
; 2. 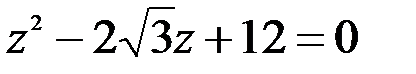 .
.
Задание №2.
1. 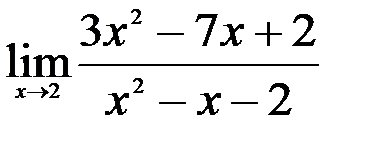 ; 2.
; 2. 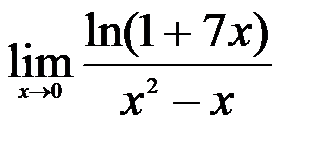 ; 3.
; 3. 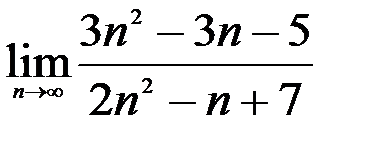 .
.
Задание №3.
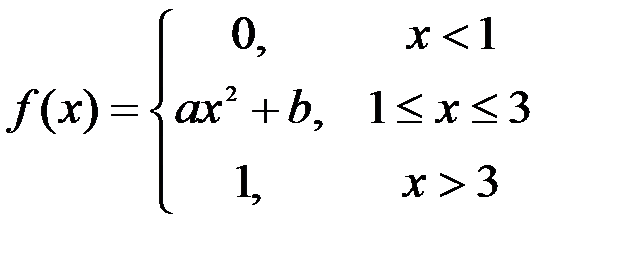 .
.
Задание №4.
1. 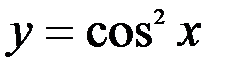 ; 2.
; 2. 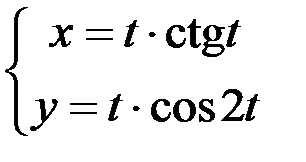 ; 3.
; 3. 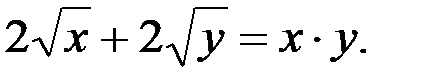
Задание №5. 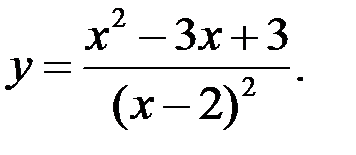
Вариант 21
Задание №1.1. 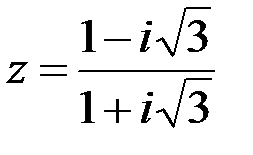 ; 2.
; 2. 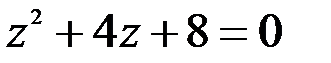 .
.
Задание №2. 1. 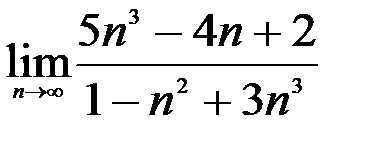 ; 2.
; 2. 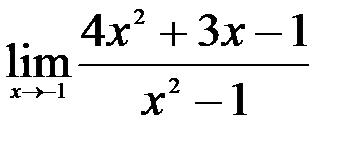 ; 3.
; 3. 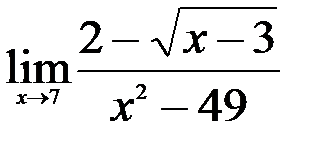 .
.
Задание №3.
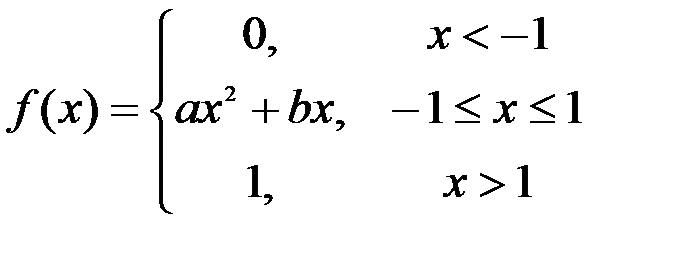 .
.
Задание №4.
1. 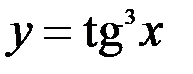 ; 2.
; 2. 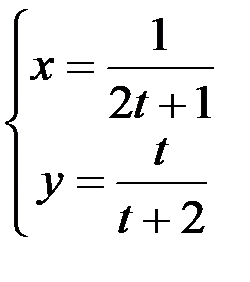 ; 3.
; 3. 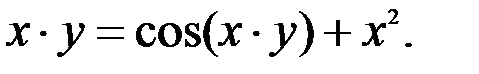
Задание №5. 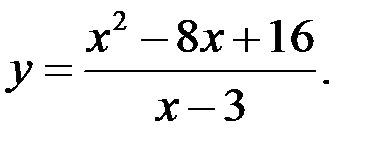
Вариант 22
Задание №1.1. 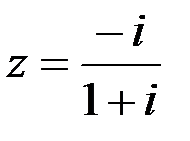 ; 2.
; 2. 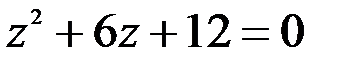 .
.
Задание №2.
1. 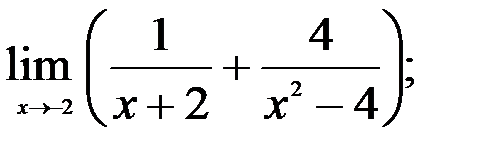 2.
2. 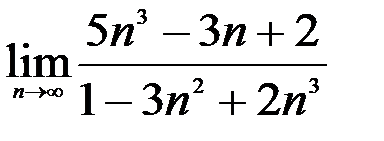 ; 3.
; 3. 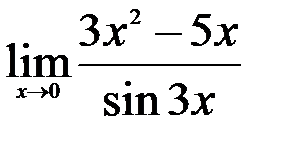 .
.
Задание №3.
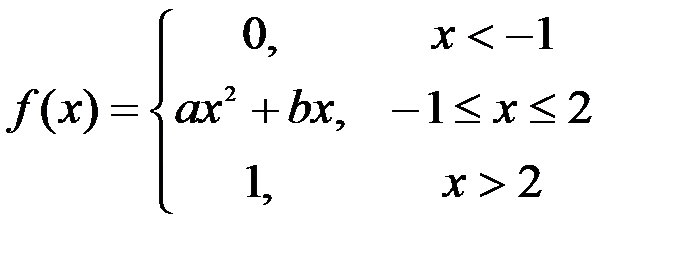 .
.
Задание №4.
1. 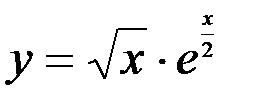 ; 2.
; 2. 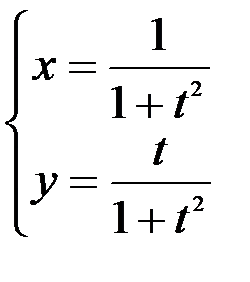 ; 3.
; 3. 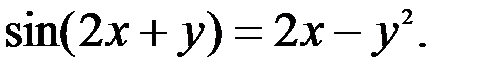
Задание №5. 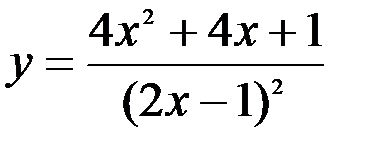 .
.
Вариант 23
Задание №1.1. 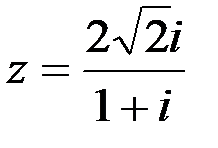 ; 2.
; 2. 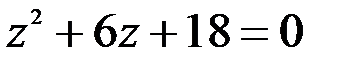 .
.
Задание №2.
1. 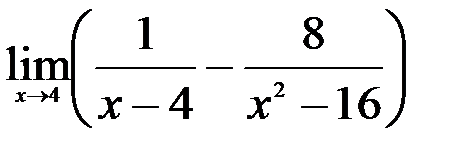 ; 2.
; 2. 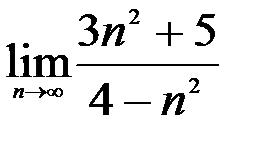 ; 3.
; 3. 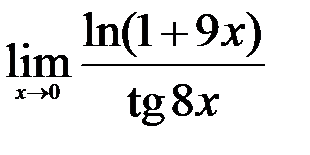 .
.
Задание №3.
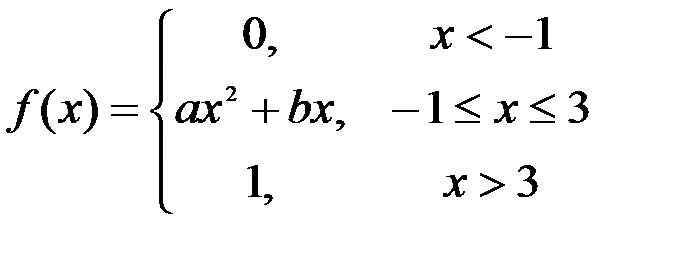 .
.
Задание №4.
1. 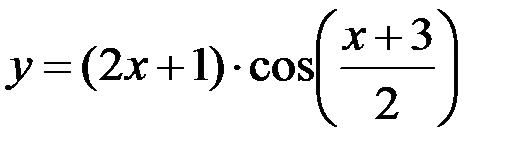 ; 2.
; 2. 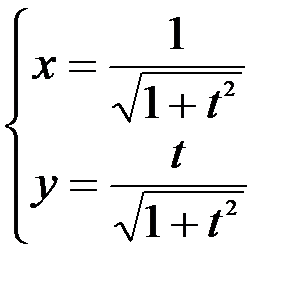 ; 3.
; 3. 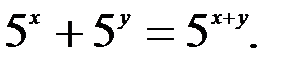
Задание №5. 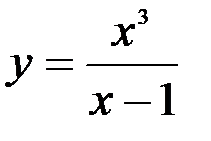 .
.
Вариант 24
Задание №1.1.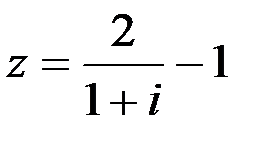 ; 2.
; 2. 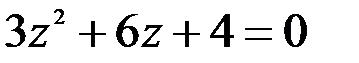 .
.
Задание №2.
1. 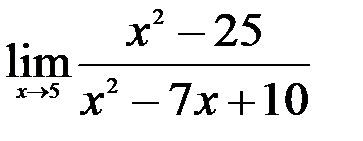 ; 2.
; 2. 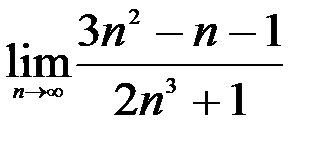 ; 3.
; 3. 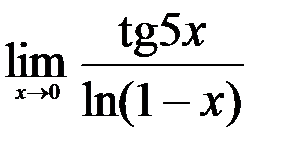 .
.
Задание №3.
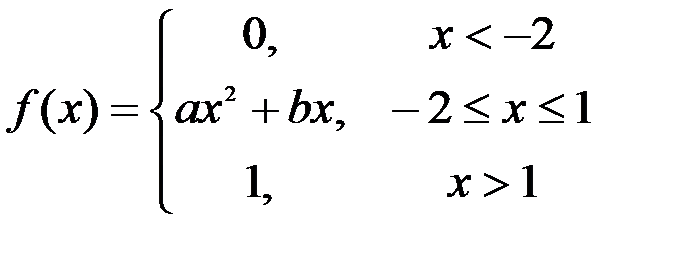 .
.
Задание №4.
1. 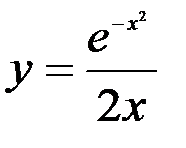 ; 2.
; 2. 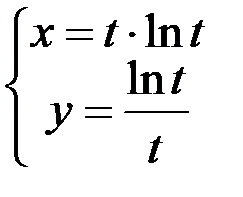 ; 3.
; 3. 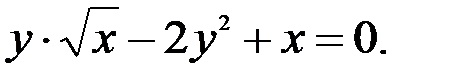
Задание №5. 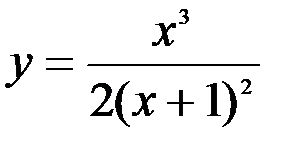 .
.
Вариант 25
Задание №1.1. 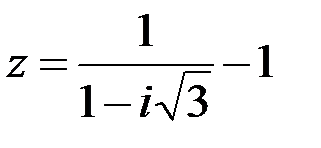 ; 2.
; 2. 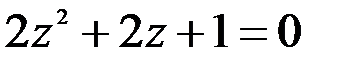 .
.
Задание №2.
1. 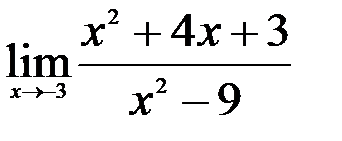 ; 2.
; 2. 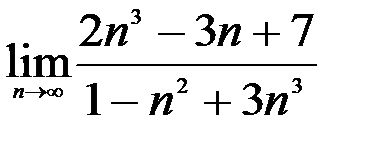 ; 3.
; 3. 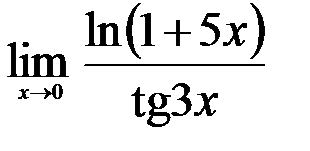 .
.
Задание №3.
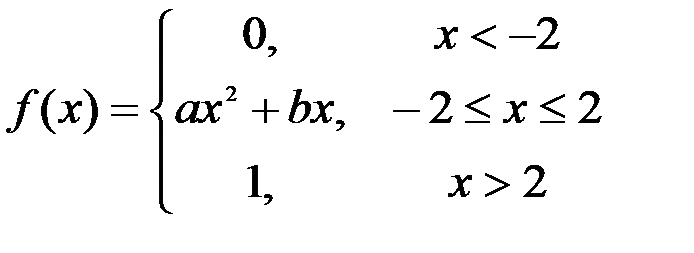 .
.
Задание №4.
1. 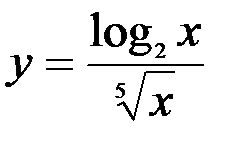 ; 2.
; 2. 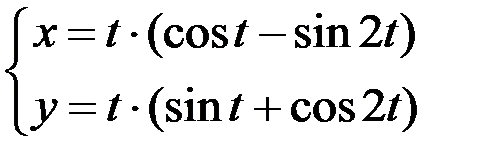 ; 3.
; 3. 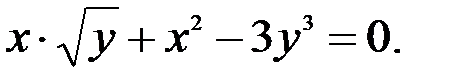
Задание №5. 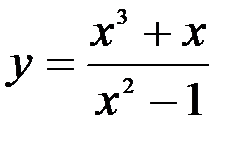 .
.
Вариант 26
Задание №1.1. 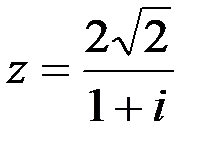 ; 2.
; 2. 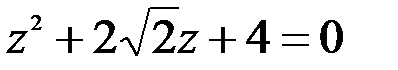 .
.
Задание №2.
1. 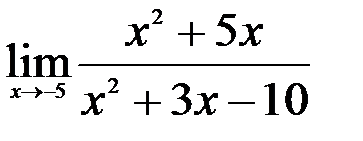 ; 2.
; 2. 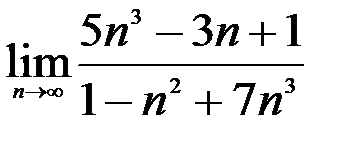 ; 3.
; 3. 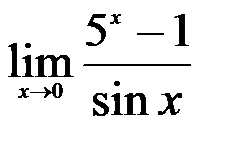
Задание №3.
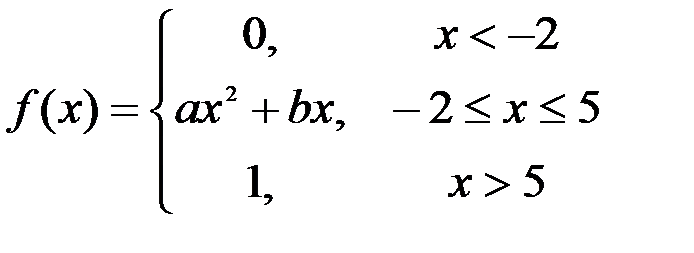 .
.
Задание №4.
1. 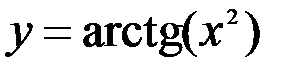 ; 2.
; 2. 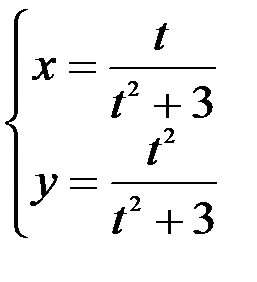 ; 3.
; 3. 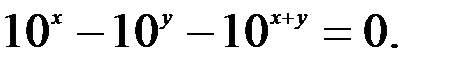
Задание №5. 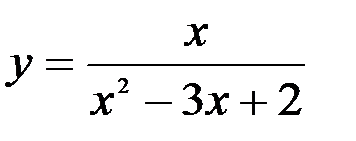 .
.
Вариант 27
Задание №1.1. 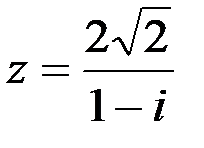 ; 2.
; 2. 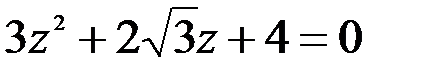 .
.
Задание №2.
1. 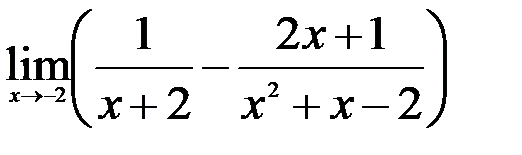 ; 2.
; 2. 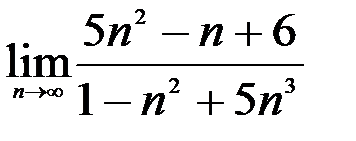 ; 3.
; 3. 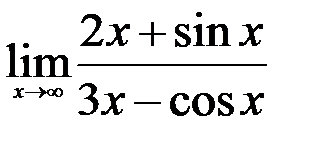 .
.
Задание №3.
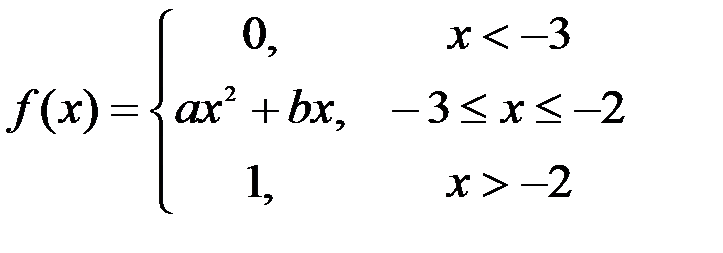 .
.
Задание №4.
1. 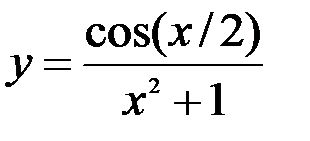 ; 2.
; 2. 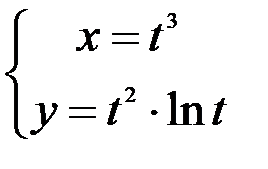 ; 3.
; 3. 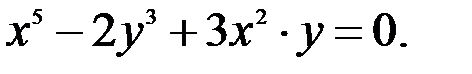
Задание №5. 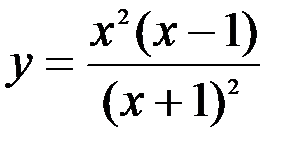 .
.
Вариант 28
Задание №1.1. 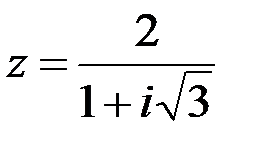 ; 2.
; 2. 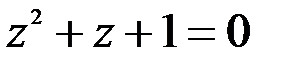 .
.
Задание №2.
1.  ; 2.
; 2. 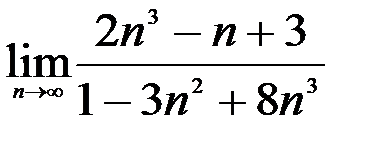 ; 3.
; 3. 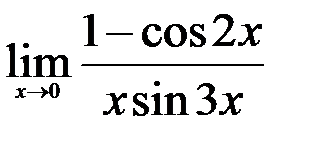 .
.
Задание №3.
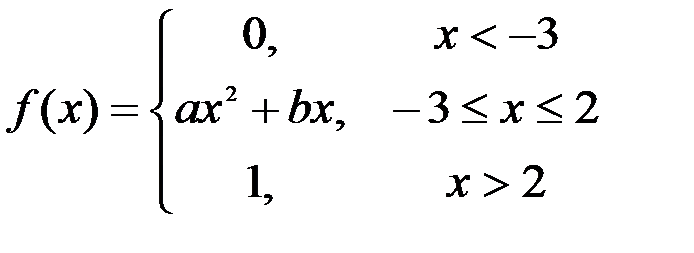 .
.
Задание №4.
1. 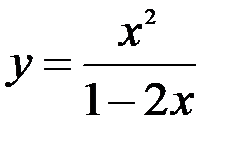 ; 2.
; 2. 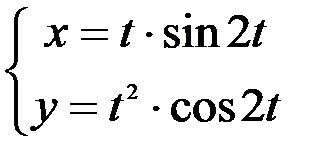 ; 3.
; 3. 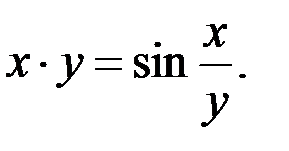
Задание №5. 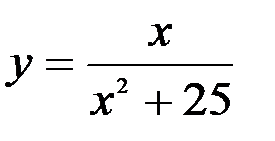 .
.
Вариант 29
Задание №1.1. 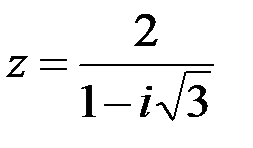 ; 2.
; 2. 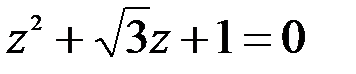 .
.
Задание №2.
1. 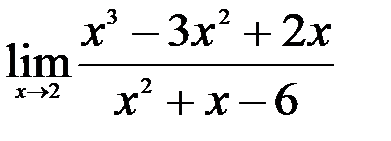 ; 2.
; 2. 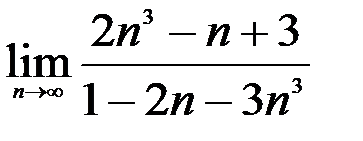 ; 3.
; 3. 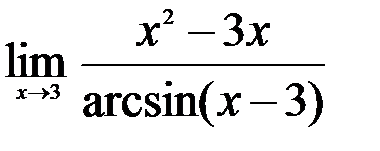 .
.
Задание №3.
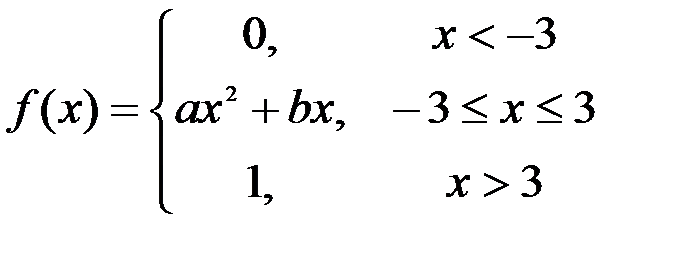 .
.
Задание №4.
1. 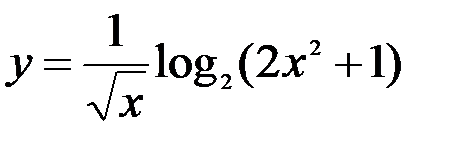 ; 2.
; 2. 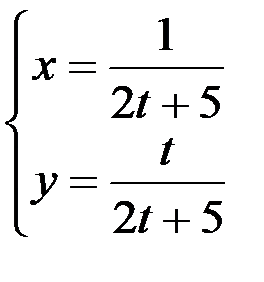 ; 3.
; 3. 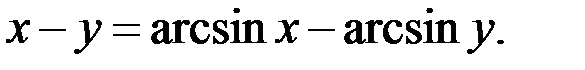
Задание №5. 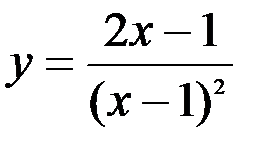 .
.
Вариант 30
Задание №1.1. 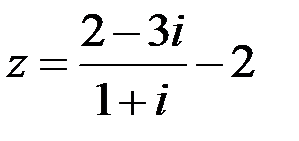 ; 2.
; 2.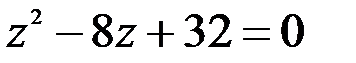 .
.
Задание №2.
1. 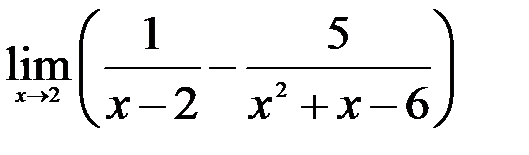 ; 2.
; 2. 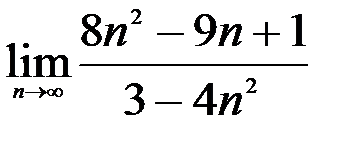 ; 3.
; 3. 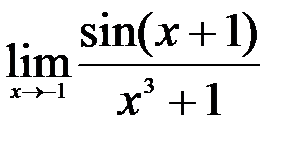 .
.
Задание №3.
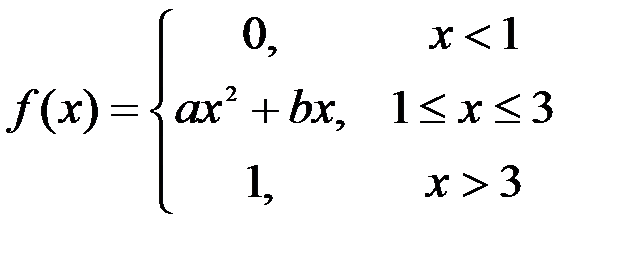 .
.
Задание №4.
1. 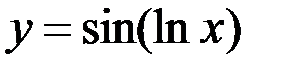 ; 2.
; 2. 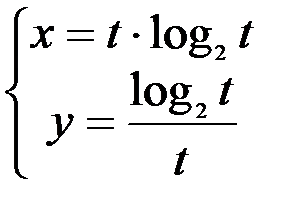 ; 3.
; 3. 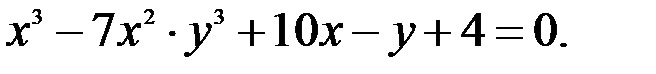
Задание №5. 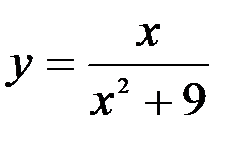 .
.
Справочный материал
Комплексные числа
Алгебраической формой комплексного числа 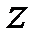 называется выражение вида
называется выражение вида 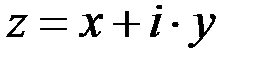 , где
, где 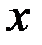 и
и 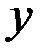 – действительные числа, а
– действительные числа, а 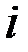 – так называемая мнимая единица (
– так называемая мнимая единица ( 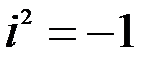 ).
).
Число 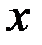 называется действительной частью комплексного числа
называется действительной частью комплексного числа 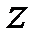 (
( 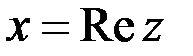 ), число
), число 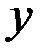 - мнимой частью
- мнимой частью 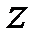 (
( 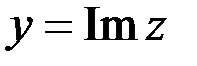 ).
).
Два комплексных числа 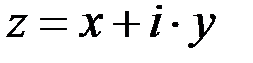 и
и 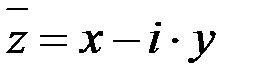 , отличающиеся лишь знаком мнимой части, называются сопряженными.
, отличающиеся лишь знаком мнимой части, называются сопряженными.
Пусть даны два комплексных числа 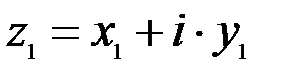 и
и 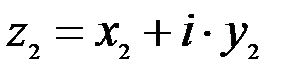 . Они равны тогда и только тогда, когда равны их действительные и мнимые части, т.е.
. Они равны тогда и только тогда, когда равны их действительные и мнимые части, т.е. 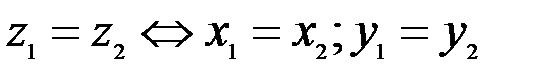 .
.
Действия над комплексными числами в алгебраической форме задаются формулами
1. 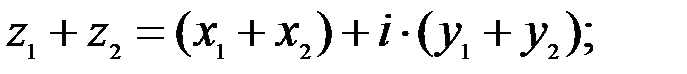
2. 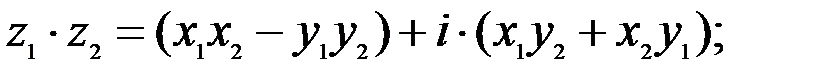
В частности 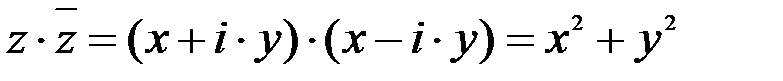 ;
;
3. 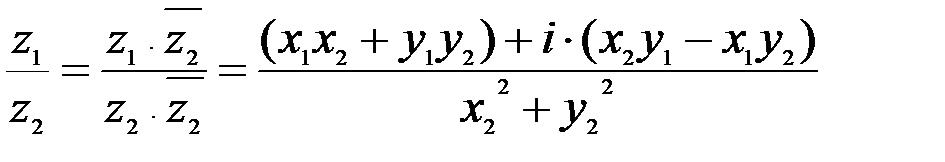 .
.
 Комплексное число
Комплексное число 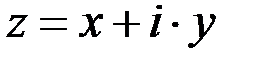 можно изобразить на плоскости
можно изобразить на плоскости 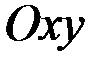 в виде точки
в виде точки 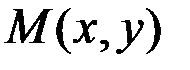 или радиус-вектора
или радиус-вектора 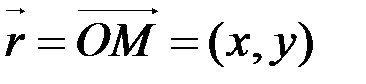 .
.
Длина вектора 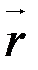 называется модулем комплексного
называется модулем комплексного 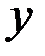
числа и обозначается 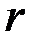 или
или 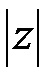 , а угол
, а угол 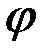 между вектором у М
между вектором у М
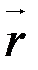 и положительным направлением оси
и положительным направлением оси 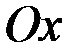 называется
называется 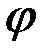
аргументом этого комплексного числа. О х х
Главным называется значение аргумента 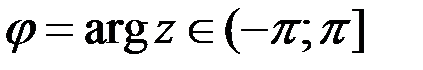 .
.
Очевидно, что 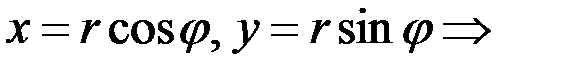
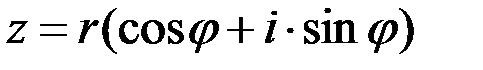 (1)
(1)
Полученная запись комплексного числа называется тригонометрической формой.
Модуль и аргумент комплексного числа определяются по формулам
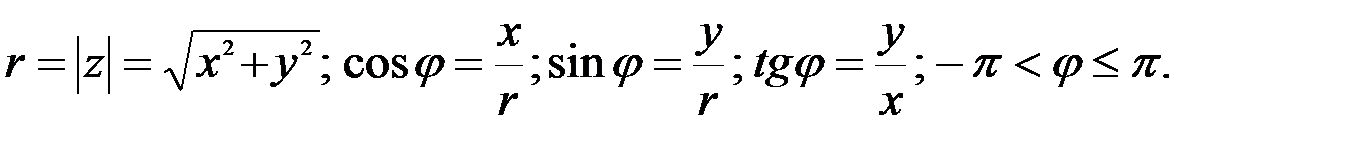
Используя формулу Эйлера 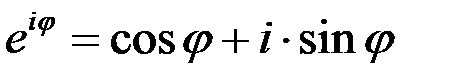
комплексное число 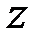 можно записать в показательной форме
можно записать в показательной форме 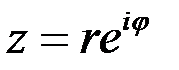 .
.
Действия над комплексными числами в тригонометрической форме выполняются по формулам:
1. 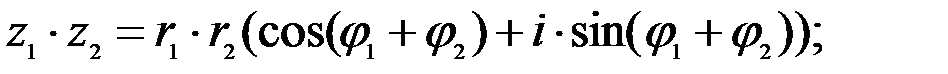
2. 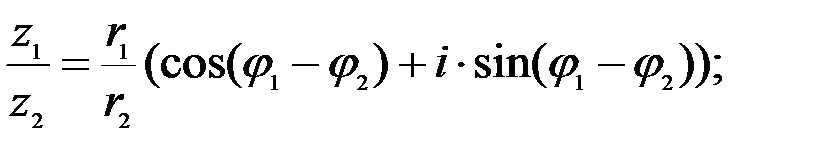
3. 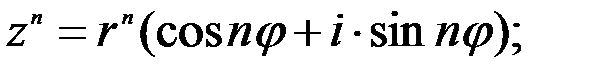 (2)
(2)
4. 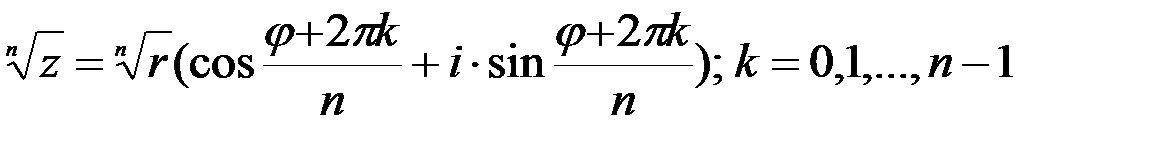 .
.
В частности 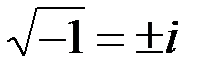 .
.
Пределы
Для нахождения пределов функции используются следующие теоремы. Если существуют пределы 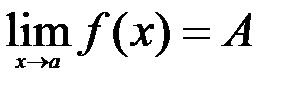 и
и 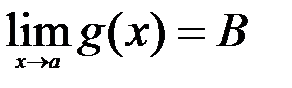 , то
, то
1. 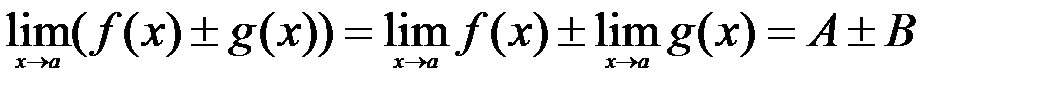 ;
;
2. 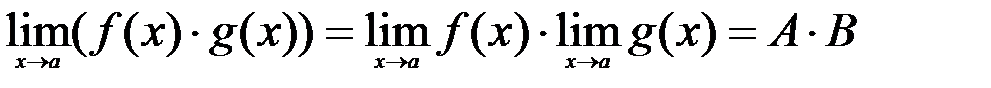 ;
;
В частности, 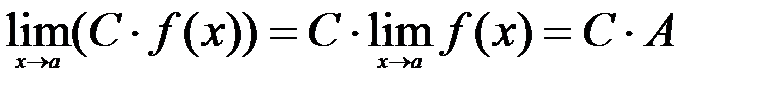 , где
, где 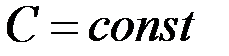 ;
;
3. 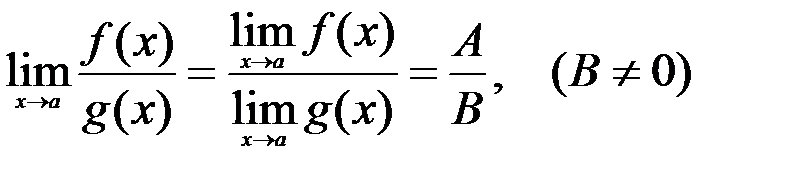 .
.
Аналогичные теоремы справедливы для пределов последовательностей.
Имеют место два замечательных предела:
1. 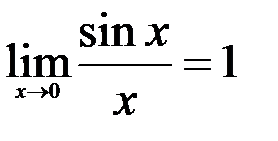 ; 2.
; 2. 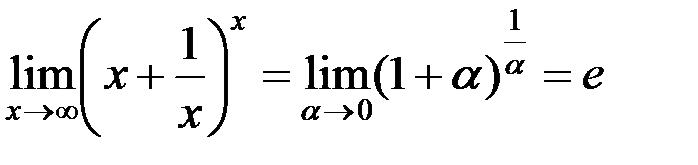 .
.
Следствия:
1. 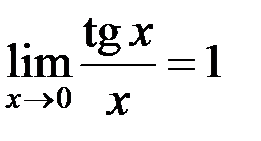 ; 2.
; 2. 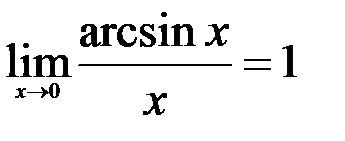 ; 3.
; 3. 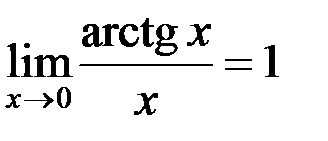 ; 4.
; 4. 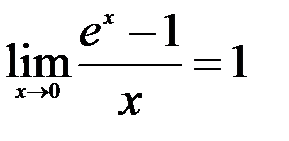
5. 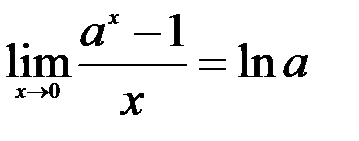 ; 6.
; 6. 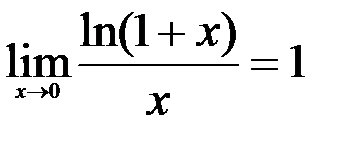 ; 7.
; 7. 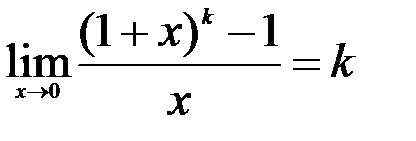 .
.
Для раскрытия неопределённостей вида 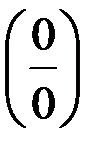 и
и 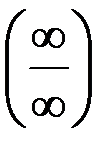 используют правило Лопиталя. Пусть функции
используют правило Лопиталя. Пусть функции 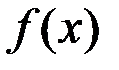 и
и 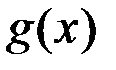 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки 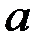 (быть может кроме неё самой);
(быть может кроме неё самой); 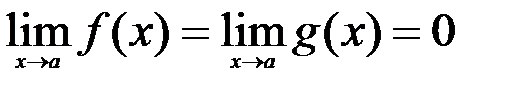 или
или 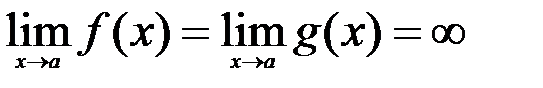 и
и 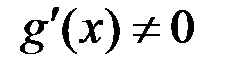 . Тогда, если существует предел
. Тогда, если существует предел 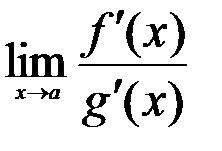 , то
, то 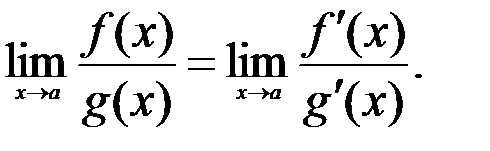 (3)
(3)
Непрерывность функции в точке
Функция 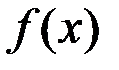 называется непрерывной в точке
называется непрерывной в точке 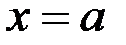 , если
, если
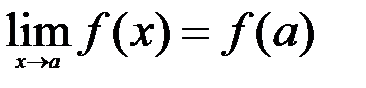 . (4)
. (4)
Указанное равенство предполагает, что функция определена в точке
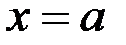 и её окрестности и имеет предел при
и её окрестности и имеет предел при 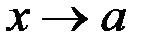 .
.
Равенство (4) эквивалентно равенству
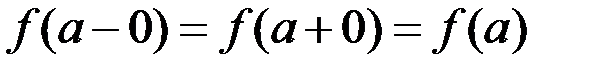 , (5)
, (5)
где 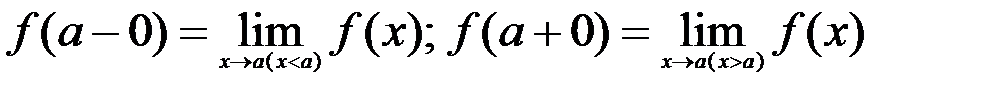 – лево и правосторонние пределы функции в точке
– лево и правосторонние пределы функции в точке 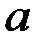 .
.
Известно, что элементарные функции непрерывны в каждой точке, в которой они определены.
Точки, в которых нарушается условие непрерывности, называются точками разрыва функции. Все точки разрыва разделяются на точки разрыва первого и второго рода.
Точка разрыва 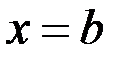 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции 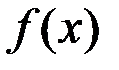 , если в этой точке существуют конечные пределы слева
, если в этой точке существуют конечные пределы слева 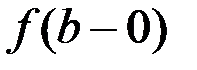 и справа и
и справа и 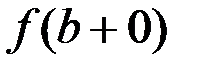 . При этом, если
. При этом, если 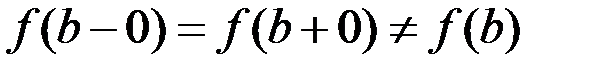 , то точка
, то точка 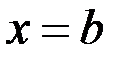 называется точкой устранимого разрыва; а если
называется точкой устранимого разрыва; а если 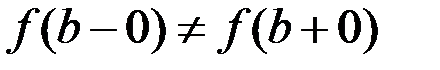 , то точкой конечного разрыва.
, то точкой конечного разрыва.
Точка разрыва 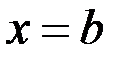 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции 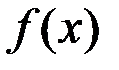 , если хотя бы один из односторонних пределов в этой точке не существует или равен бесконечности.
, если хотя бы один из односторонних пределов в этой точке не существует или равен бесконечности.
Производная
Правила дифференцирования
Пусть 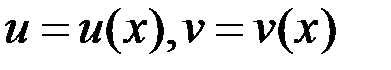 , тогда
, тогда
1. 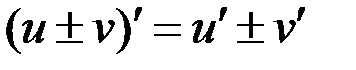 ;
;
2. 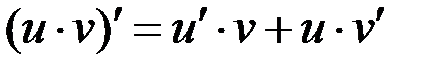 ; в частности:
; в частности: 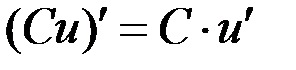 ,
, 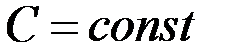 ;
;
3. 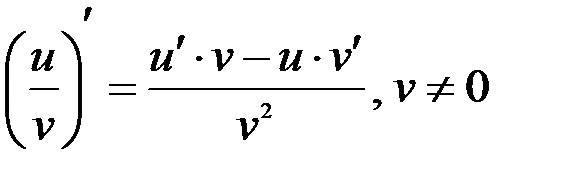 ;
;
4. если 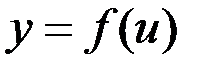 , где
, где 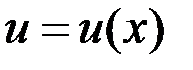 , тогда
, тогда 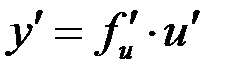 .
.
Таблица производных
1. 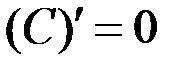 ; 2.
; 2. 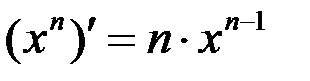
3. 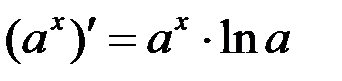 ; в частности:
; в частности: 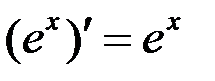 ;
;
4. 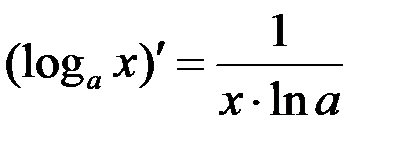 ; в частности:
; в частности: 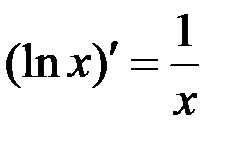 ;
;
5. 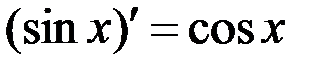 ; 6.
; 6. 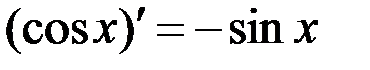 ;
;
7. 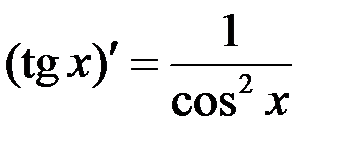 ; 8.
; 8. 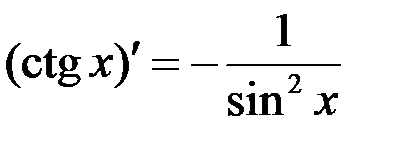 ;
;
9. 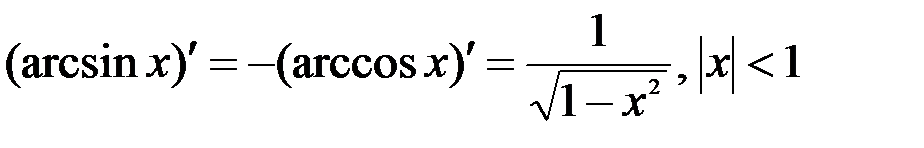 ;
;
10. 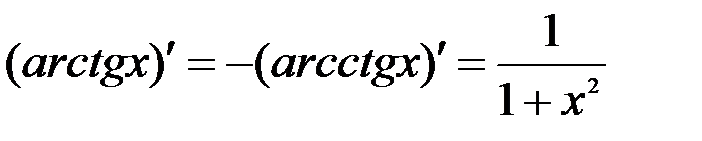 .
.
5. Исследование функции и построение её графика
Основные свойства функций
1.Функция 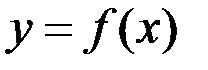 называется возрастающей (убывающей) на множестве
называется возрастающей (убывающей) на множестве 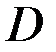 , если для любых
, если для любых 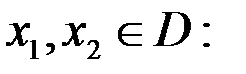
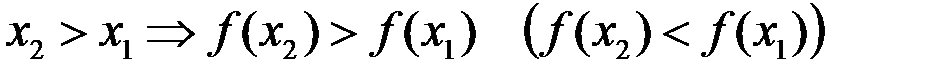 .
.
2. Функция 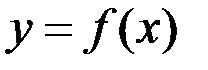 называется периодической, если существует число
называется периодической, если существует число 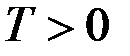 такое, что
такое, что 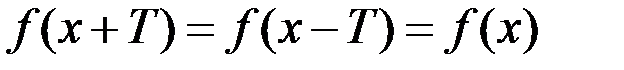 .
. 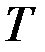 –периодфункции.
–периодфункции.
3. Функция 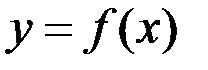 называется четной, если
называется четной, если 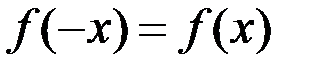 . График четной функции симметричен относительно оси
. График четной функции симметричен относительно оси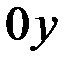 . Функция
. Функция 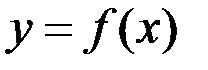 называется нечетной, если
называется нечетной, если 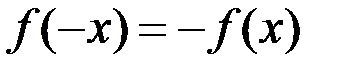 . График нечетной функции симметричен относительно начала координат.
. График нечетной функции симметричен относительно начала координат.
Четная и нечетная функция должна иметь область определения симметричную относительно начала координат.
